Oft zielt deine Hypothese dann darauf ab, zu untersuchen, ob es einen Unterschied dieser Variablen zwischen zwei Gruppen (z.B. Männer und Frauen) oder auch zwischen zwei Messwiederholungen (z.B. vor und nach der OP) gibt. Die Nullhypothese lautet in dem Fall dann „Es gibt keinen Lageunterschied zwischen den beiden Gruppen“ bzw. „Es gibt keinen Lageunterschied zwischen den beiden Messwiederholungen“. Der Signifikanztest versucht, diese Nullhypothese abzulehnen. Mit einem signifikanten p-Wert (p kleiner 5 %), wird genau das erreicht: ein signifikanter Unterschied wird nachgewiesen.
Aber welche Methode genau passt nun für diesen Test auf Lageunterschied?
Es gibt verschiedene Methoden, die verwendet werden können, um die Werte einer metrischen Variable von zwei Gruppen oder zwei Messwiederholungen auf Unterschied in der Lage zu untersuchen. Die Wahl des Tests hängt von der Art und der Verteilung der Daten ab.
Folgende Fragen musst du klären:
- Sind die Gruppen verbunden oder unverbunden?
- Sind die Werte für beide Gruppen normalverteilt? (zumindest wenn es sich um eine metrische Messung handelt)
- Falls unverbunden und normalverteilt: Sind die Varianzen gleich?
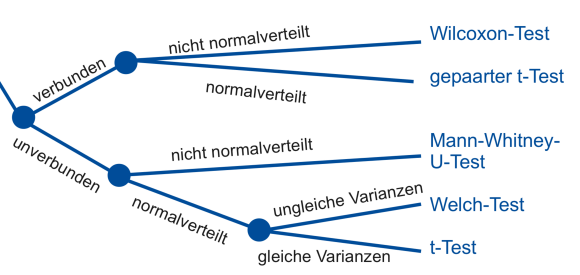
In folgendem Entscheidungsbaum siehst du, wie die Methode ausgewählt wird:
Ob die Daten verbunden oder unverbunden sind, entscheidest du über dein Studiendesign. Wenn du die Zielvariable zweimal am gleichen Unterschungsobjekt erhoben hast (z.B. bei Messwiederholungen, vor und nach der OP), dann sind die Daten verbunden. Wenn die Untersuchungsobjekte nur einmal gemessen wurden, sich aber in zwei verschiedenen „Töpfen“ befinden (z.B. Männer und Frauen), sind die Daten unverbunden.
Die Normalverteilung wird mittels Normalverteilungsplots (Q-Q-Plot, Q-Q-Diagramm) oder geeigneter Tests (z.B. Shapiro-Wilk-Test, Kolmogorov-Smirnoff-Test) untersucht. Ich empfehle generell eher die Normalverteilungsplots (Q-Q-Plot, Q-Q-Diagramm), da das Ergebnis der Tests auf Normalverteilung stark von der Fallzahl abhängt.
Die Entscheidung, ob bei den unverbundenen, normalverteilten Daten gleiche Varianzen vorliegen oder nicht, kannst du über einen Test auf Varianzhomogenität (z.B. Levene-Test) treffen. Oder du arbeitest hier deskriptiv und betrachtest die beiden Standardabweichungen.
Besonderheit ordinale Daten
Ist die Variable, die auf Lageunterschied untersucht werden soll, ordinal, so wird direkt die nicht-parametrische Methode (Wilcoxon, Mann-Whitney-U) verwendet werden. Eine Normalverteilung wird bei ordinalen Variablen nicht geprüft. Um ordinale Daten mit diesen Tests auf Lageunterschiede verwenden zu können, sollte sie nicht zu wenige Abstufungen haben. Also nicht beispielsweise nur 3 Stufen: klein/mittel/groß. Besser sind Variablen, die z.B. auf 7 Stufen oder mehr gemessen wurden. Dafür eignen sich die Tests auf Lageunterschiede besser.
Nicht vergessen: Deskriptive und Abbildungen
Grundsätzlich muss vor der Durchführung eines Tests die deskriptive Statistik berechnet werden. Das heißt, für beide Gruppen werden Mittelwert, Standardabweichung, Median, Interquartilsabstand berechnet. Außerdem empfehle ich, ein Diagramm mit zwei Boxplots oder Mittelwertsdiagramme mit Fehlerbalken zu erstellen. Anhand der Lage und Höhe der Boxen oder Streuungen lässt sich bereits erkennen, ob es in den Daten einen deutlichen Unterschied gibt.
Methodenauswahl
Hier nochmal die Auswahl der Tests im Überblick:
- Sind die Stichproben unverbunden und normalverteilt, so wird der t-Test durchgeführt. Der t-Test setzt zusätzlich Gleichheit der Varianzen voraus, was zum Beispiel mittels Levene-Test untersucht wird. Sind die Varianzen nicht gleich, wird der Welch-Test verwendet.
- Sind die Stichproben unverbunden und nicht normalverteilt oder ordinal, so wird der Mann-Whitney-U Test verwendet.
- Sind die Stichproben verbunden und normalverteilt, so wird der gepaarte t-Test durchgeführt.
- Sind die Stichproben verbunden und nicht normalverteilt oder ordinal, so nimmt man den Wilcoxon-Test.
Alle Tests geben die jeweilige Teststatistik und den p-Wert zurück. Ist der p-Wert kleiner als 0,05, so gibt es einen signifikanten Unterschied (signifikant auf dem Niveau 5 %). Ist der p-Wert größer als 0,05, so kann kein signifikanter Unterschied nachgewiesen werden (was nicht heißt, dass es keinen gibt).
Ergebnisse berichten
Berichtet wird zusätzlich zum p-Wert meist die Teststatistik (z.B. t oder z) und manchmal die Freiheitsgrade (wenn es sie gibt). Sinnvoll ist es außerdem, die Effektstärke zu berechnen (z.B. Cohens d), um zusätzlich zur Signifikanz noch eine Aussage zur Stärke des Unterschieds treffen zu können.
Mehr Gruppen vergleichen und mehr statistisches Know-How
Willst du mehr über weitere Gruppenvergleiche lernen oder hast Probleme, die passenden Methoden für andere Situationen auszuwählen? Dann hol dir mein Statistik-Starter-Paket gratis zum Download. Du findest in einem PDF und mehreren begleitenden Videos eine verständliche und praxisnahe Einführung in die grundlegenden statistischen Konzepte und lernst, die passenden Methoden für deine Datenanalyse sicher und zuverlässig auszuwählen.
Willst du noch mehr Material und gleich tiefer einsteigen? Dann passt die Statistik-Akademie gut für dich. Dort findest du zahlreiche Videos und Softwaretutorials, in denen ich dir verschiedenste statistische Methoden und Themen verständlich erkläre und dir auch die Umsetzung mit Software (R, SPSS, DATAtab, G*Power) zeige. Dazu bekommst du Handouts, Checklisten, Beispieldaten, SPSS-Syntax und R-Codes zum Download. Und im FAQ und Lexikon klärst du deine offenen Fragen zur Statistik ganz einfach selbst.
Interessiert? Dann schau dir die Statistik-Akademie hier genauer an (klick).
Die 10 häufigsten Fehler bei Abschlussarbeiten mit SPSS und wie du sie vermeidest.
Hol dir jetzt die Liste für 0,- Euro und komm mit deiner Datenanalyse fehlerfrei und schnell voran!

Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.





Welches statistische Analyseverfahren wende ich an bei der Inhaltliche Zusammenhangshypothese: „Je besser das Rehabilitationskonzept auf die Ressourcen der Rehabilitanden abgestimmt ist, umso größer ist die Zufriedenheit der Rehabilitanden.“ und der Inhaltliche Unterschiedshypothese: „Jüngere Patienten mit chronischen Rückenschmerzen leiden seltener an einem metabolischen Syndrom als ältere Patienten.“
Hallo Christina,
das kommt auf das Messniveau der einzelnen Parameter an und auf die Verteilung.
Schöne Grüße
Daniela
Hallo Frau Keller,
viellen Dank für Ihre tolle Seite!
Ich habe noch Fragen zum Thema.
Da wir nicht-parametrische Daten vorliegen haben, nutzten wir zunächst den Kruskal-Wallis Test, um zu prüfen, ob sich unsere Gruppen signifikant voneinander unterscheiden. Nach signifikantem Ergebnis, wollten wir wissen, zwischen welchen Gruppen signifikante Unterschiede auftraten und prüften dies mit einzelnen Man-Whitney-U Tests. Diese Tests beruhen auf Medianen, wenn ich es richtig verstanden habe. Nun meine Fragen:
Wie ich im Verlauf der Kommentare herausgelesen habe, berichte ich nur die Mediane in meiner Arbeit und verzichte auf den Bericht von Mittelwerten. Demenstprechend erstelle ich Liniendiagramme auch auf Grundlage der Mediane und nicht von Mittelwerten, oder? Wenn dem so ist, gibt es dann die Möglichkeit Konfidenzintervalle zu berechnen, um diese als Fehlerbalken in meine Grafik einzutragen? Bzw. gibt es dann eine andere Variante für die Fehlerbalken?
Ich danke Ihnen im Voraus für die Unterstützung!
Hallo Judith,
als Darstellungsform eignet sich hier gut der Boxplot, ist allerdings nicht wie ein Konfidenzintervall zu interpretieren.
Schöne Grüße
Daniela
Hallo Daniela!
Ich habe da ein kleines Problem mit einer Aufgabe…
Ich soll eine Rangliste von fünf Klassen erstellen. Die Klassen haben alle eine unterschiedliche Anzahl von Schülern und natürlich haben alle einen unterschiedlichen Notenschnitt. Wie kann ich unter diesen Umständen errechnen welche die „beste“ Klasse ist? Ich habe mal den Mittelwert errechnet, aber ist der das richtige Mittel wenn man bedankt, dass die Klassen unterschiedlich groß sind?
Für einen Tipp wäre ich sehr dankbar!
Gruß,
Stephanie
Hallo Stephanie,
das kommt darauf an, wie man die „beste“ Klasse definiert. Meiner Ansicht nach passt der Mittelwert. Die unterschiedliche Klassengröße ist kein Problem.
Weitere Fragen könnt ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela,
Ich muss für meine BA eine Messung mit mehren Zahlenwerten mit einer anderen Messung, die wiederum genauso viel Zahlenwerte beinhaltet vergleichen.
Wissen Sie zufällig wie ich statistisch korrekt vorgehe um eine Aussage über den Vergleich beider Messungen zu erlangen, zb. dass beide Messungen ähnliche Werte haben oder eine Messung hat deutlich größere Werte als die Andere?
Bis jetzt war meine Idee den Mittelwert der Messungen zu betrachten, aber ich würde sagen, dass das nicht sinnvoll wäre aufgrund der Vielzahl der Werte.
Vielen Dank für deine Mühen.
Liebe Grüße Basti
Hallo Basti,
das hört sich schon nach einem „Lageunterschied“ an, was Du hier untersuchen willst. Wenn die Daten symmetrisch sind, dann passt auch der Mittelwert. Am besten noch mit einem Test prüfen, damit das Ergebnis auch aussagekräftig ist.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela,
ich hätte die Frage, wie ich mit unterschiedlichen Stichproben bei einer Interventionsstudie umgehen soll. Es wurde ein Fragebogen zur Einstellung verteilt, anschließend wurde eine Fortbildung durchlaufen und danach der Fragebogen noch einmal ausgefüllt. Das Problem ist, dass ein erheblicher Teil der Stichprobe beim zweiten Testzeitpunkt nicht geantwortet hat, dafür haben den Fragebogen Fortbildungsteilnehmer ausgefüllt, die zum ersten Testzeitpunkt nicht teilgenommen hatten. Wie ist hier vorzugehen? Welcher Test ist möglich? Kann ich nur mit der sehr kleinen Reststichprobe rechnen, die an beiden Zeitpunkten teilgenommen hat?
Vielen Dank, dass ich meine Fragen hier stellen kann!
Viele Grüße
Juli
Hallo Juliane,
hier kannst Du leider nur die vollständigen Fälle verwenden, zumindest, wenn Du Tests rechnen willst. Die erlauben kein Mischen von verbundenen und unverbundenen Stichproben, wie das bei Dir der Fall wäre, wenn Du alle verwendest.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Frau Keller,
ich habe eine Stichprobe von n =51 Personen. Für alle Patienten habe ich eine Angabe zu subjektiv empfundenen Schmerzen im Anamnesegespräch (Variable: Schmerzen in der Anamnese= ja/nein) und jeweils eine Angabe zu Schmerzenparametern in der Diagnostik (Variable: Schmerzenoarameter in der Diagnostik vorhanden? = ja/nein). Ich möchte gerne herausfinden, ob Patienten, die in der Anamnese Schmerzen angeben, auch in der Diagnostik Schmerzen aufweisen. (H0: Es besteht kein Zusammenhang zwischen den Angaben in der Anamnese und dem objektiven Befund in der Diagnostik, H1: Es besteht ein Zusammenhang). Da es sich jeweils um kategoriale Variablen handelt, würde ich eine Kreuztabelle anlegen. Handelt es sich aber um eine verbundene Stichprobe, bei der ich den Mc Nemar Test anwende? Oder handelt es sich um eine unverbundene Stichprobe, bei der ich einen Chi²-Test nutze? Für eine Antwort wäre ich sehr dankbar.
Hallo Meike,
ich würde sagen das sind unverbundene Parameter und deshalb Fishers Exakter Test (Chi-Quadrat würde ich nur bei größer als 2×2-Tabelle nutzen).
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela, leider ist meine Statistik-Erinnerung extrem ausgelöscht, so daß ich trotz des Schaubildes und Wiki immer noch nicht weiß welchen Test ich anwenden kann.
Wir vergleichen zwei Quellen, in denen wir gezählt haben – absolut und prozentual – wie viele positive, neutrale und negative (evtl. mit Abstufung auch 5 Kategorien) Meldungen vorkommen.
Wie können wir herausfinden ob die Quellen signifikant unterschiedliche Anzahlen haben?
Danke und viele Grüße
martin
Hallo Martin,
was sind Eure Untersuchungsobjekte? Die Meldungen in den Quellen? Dann habt Ihr als Beobachtungen in den Daten stehen „positiv“, „neutral“, „negativ“ usw. Dann sind das ordinale Daten. Wenn Ihr die zwischen den beiden Quellen vergleicht (unabhängige Stichproben), müsste das der Mann-Whitney U Test sein.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo ich habe eine kurze Frage:
Ich habe eine Stichprobe bei der Schüler die wahrgenommene Unterstützung von 3 unterschiedliche AKTEURE bewerten sollten.
Ich habe nun bereits für jede Unterstützung eine Skala, also insgesmat 3 Skalen gebildet und möchte nun diese 3 miteinander vergleichen. Meine Hypothese lautet: Es bestehen Unterschiede hinsichtlich der Wahrnehmung der Unterstützung von Akteur 1, 2, und 3.
Alle Skalen sind nicht normalverteilt.
Welchen Test kann ich hierfür anwenden?
vielen Dank für die Hilfe!
Hallo Carola,
die Antwort auf diese Frage findest Du in meinem kostenlosen E-Book: https://statistik-und-beratung.de/gratis-e-book-statistische-datenanalyse-die-grundlagen/
Schöne Grüße
Daniela
Hallo Daniela,
ich habe für 2 Gruppen zu je 14 Zeitpunkten den Blutdruck erhoben. Meine Daten sind nicht normalverteilt. Mittels Mann-Whitney-U habe ich bereits heraussgefunden, dass sich die beiden Gruppen zu jedem einzelnen Zeitpunkt unterscheiden. Nun würde mich interessieren ob trotzdem der Verlauf über die Zeit gleich ist? Mit welchem Test im SPSS finde ich das denn heraus?
Vielen Dank für deine Mühen.
lg Anne
Hallo Anne,
bei Normalverteilung wäre das der Interaktionseffekt von Zeit und Gruppe in einer mehrfaktoriellen ANOVA. Da die Daten nicht normalverteilt sind, kannst Du die aber nicht verwenden. Ich würde versuchen, über die Differenzwerte zu arbeiten (das geht dann immer nur für 2 Zeitpunkte, aber vielleicht reicht das ja aus).
Schöne Grüße
Daniela
Hallo Daniela,
zunächst einmal ein Dankeschön für das Beantworten von den vielen Fragen hier.
Meine Frage lautet wie folgt:
Ich habe zwei (unabhängige) Stichproben die ich bzgl. Mittelwert vergleichen möchte.
– Stichprobe 1: n=53, nicht normalverteilt
– Stichprobe 2: n=43, nicht normalverteilt
– Varianzen signif. unterschiedlich
Demnach müsste man wohl den Mann-Whitney-U-Test verwenden. Nun aber die Frage, ob man auch den t-Test verwenden darf, da n>30?
Habe mal beides probiert mit extrem unterschiedlichen Signifikanzaussagen :-/.
Besten Dank im Voraus und viele Grüße
Mario
Hallo Mario,
bei n>30 gilt der t-Test robust auf Abweichungen von der Normalverteilung, wenn die Varianzen gleich sind. Passt also hier nicht. Demnach den MWU-Test verwenden.
Weitere Fragen gern in der Facebookgruppe Statistikfragen posten: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Vielen lieben Dank 🙂
Hallo Daniela,
ich versuche gerade mit SPSS zu überprüfen, ob die Ergebnisse einer Fragebogenerhebung mit einer objektiven Datenerhebung übereinstimmen oder ob sich die subjektiv und objektiv erhobenen Daten unterscheiden.
Ist es möglich, dazu einen Wilcoxon-Test zu machen? (Aufgrund der geringen Stichprobengröße wollte ich keinen t-Test machen). Ich bin mir aber nicht sicher ob das zulässig ist, weil ich beim Fragebogen ja eine Skala von -5 bis +5 (Likert-Skala) habe und das dann mit einer Intervallskalierung in cm vergleichen möchte. Muss ich das erst transformieren? Und darf ich nach einer z-Transformation dann einen Wilcoxon-Test machen?
Vielen Dank, Bettina
Hallo Bettina,
wenn die Daten auf unterschiedlichen Skalen erhoben wurden, muss in eine einheitliche Skala transformiert werden.
Schöne Grüße
Daniela
Hallo Frau Keller,
nette Website. Ich habe eine Frage zur Übersicht der Testmöglichkeiten. Es ist kein Test im Schaubild, der für den Vergleich unabhängiger, nicht normalverteilter Daten mit ungleichen Varianzen eingesetzt werden könnte.
Könnten Sie für diesen Fall auch einen Test vorschlagen?
Schöne Grüße
Jochen
Hallo Jochen,
bei nicht normalverteilten Daten werden die nicht-parametrischen Methoden (z.B. Mann-Whitney U, Kruskal-Wallis) verwendet. Die haben keine Anforderung an die Verteilung der Daten, auch nicht an die Varianzen. Die werden also auch verwendet, wenn die Varianzen ungleich sind.
Schöne Grüße
Daniela
Hallo Daniela,
ich führe für meine Masterarbeit eine Studie durch, bei der jeder Proband zu 5 Marken bestimmte Konstrukte z.B. seine Einstellung, Vertrauen, Kenntnis etc. bewerten muss. Jede Marke wird dabei nacheinander innerhalb eines Fragebogens anhand dieser Konstrukte bewertet (jeder Proband sieht und bewertet 5 Marken). Nun bin ich mir unschlüssig welches Testverfahren ich anwenden soll, um herauszufinden ob es signifikante Unterschiede zwischen den Marken bei der Ausprägung der abgefragten Konstrukte (Einstellung, Vertrauen, Kenntnis etc.) gibt. Ich wäre dir sehr dankbar, wenn du mir hier weiterhelfen könntest.
Vielen herzlichen Dank,
Saskia
Hallo Saskia,
du willst also z.B. „Einstellung“ zwischen den 5 Marken vergleichen? Wenn Einstellung metrisch gemessen wurde und normalverteilt ist, dann wäre das die ANOVA mit Messwiederholung, ohne Normalverteilung der Friedman-Test.
Schöne Grüße
Daniela
Hallo Daniela,
bisher habe ich keine Antwort auf mein Problem gefunden und hoffe sehr, dass du mir helfen kannst.
Ich möchte Geschwisterpaare untersuchen. Zuerst möchte ich Werte wie das Körpergewicht des einen Geschwister mit dem Körpergewicht seines Bruders/Schwesters vergleichen, später separiere ich die Geschwister mit anderen Geschwistern in 2 Gruppen. Welche Tests kann ich denn anwenden, um Werte zwischen den Geschwistern und dann zwischen den beiden Gruppen zu vergleichen?
Vielen vielen Dank für deine Hilfe!
Claudia
Hallo Claudia,
wie genau werden die aufgeteilt? Sind in den Gruppen die Geschwisterpaare drin, oder sind die verteilt…?
Schöne Grüße
Daniela
Hallo Daniela,
die Geschwister möchte ich in verschiedene Gruppen verteilen.
Danke für deine Antwort.
Claudia
So dass in jeder Gruppe jeweils ein Geschwisterteil ist? Dann sind das verbundene Stichproben.
Liebe Daniela,
ich möchte die Reduktion zwischen zwei Gruppen vergleichen (4 Gruppen).
Gruppe A mean 5,26x10E7 ±3.9x10E7 n=28
Gruppe B mean 1.6x10E7 ±1.5x10E7 n=25
Gruppe C mean 3.2x10E7 ±1.2x10E7 n=30
Gruppe D mean 9.8x10E6 ±7.3x10E6 n=32
Die Differenz zwischen A und B und zwischen C und D ist p<0.0001. Wie berechne ich ob der Differenzunterschied zwischen A / B und C / D signifikant ist?
Herzlichen Dank, Irma
Hallo Irma,
dazu kannst du entweder Kontraste definieren (in SPSS geht das z.B.) oder neue Gruppen bilden und die miteinander vergleichen.
Weitere Fragen kannst du gern in meiner Facebookfruppe Statistikfragen stellen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Liebe Daniela,
vielen Dank auch von mir für die tolle Unterstützung, die du hier anbietest!
Vielleicht kannst du mir bei meinem Problem auch helfen. Mithilfe einer mixed ANOVA untersuche ich die Wirksamkeit eines Therapieverfahrens. Ich erhebe dazu eine intervallskalierte abhängige Variable in einer Interventions- und einer Kontrollgruppe zu drei Messzeitpunkten (Prä, Post, Follow-up). Die Hypothesen lauten, dass a) über die Therapie kurzfristige Effekte erzielt werden und diese b) langfristig stabil bleiben. Meine Frage ist nun, ob ich das anhand des Verfahrens überhaupt prüfen kann oder ob dazu weitere Berechnungen wie unabhängige t-Tests notwendig sind. Über eine Antwort wäre ich sehr dankbar.
Viele Grüße
Annika
Hallo Annika,
ja, ich denke auch, dass du für die genaue Prüfung der Hypothesen noch weitere Analysen brauchst. Eventuell mixed ANOVAs mit jeweils nur 2 Zeitpunkten (prä/post und prä/FU).
Weitere Fragen kannst du gern in meiner Facebookfruppe Statistikfragen stellen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela
ich hoffe, dass ich mit meiner Frage hier an der richtigen Stelle bin.
Es geht um folgendes:
Ich habe eine Stichprobengröße von n=66. Diese 66 Befragten haben zur gleichen Zeit bzw. unmittelbar nacheinander zu drei unterschiedlichen aber vergleichbaren Produkten eine Preisschätzung abgegeben. So wie ich es verstehe sind diese Daten demnach abhängig voneinander. Kann ich dennoch eine einfaktorielle Varianzanalyse (ohne Messwiederholung) durchführen? Oder kommt hierfür sogar ein anderer Test auf Signifikanz infrage?
Freundliche Grüße
Tommy
Hallo Tommy,
das sind verbundene Stichproben und die brauchst deshalb eine Methode für Messwiederholungen.
Für weitere spezielle Fragen – nicht direkt zum Blogbeitrag hier – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
ich habe 2 Gruppen (m/w), bei denen ich Thrombozyen in die Bereiche 0 – 60, 61 – 120 und 121 bis unendlich gruppiert habe. Wenn ich das richtig verstanden habe, habe ich also eine Ordinalskalierung mit 3 Ausprägungen. Welchen Test nehme ich da? Den U test? Was sagt er dann genau aus? Wenn ich nur 2 Ausprägungen wie Groß/Klein hätte, würde ich bei signifikanz ja sagen können, dass m mehr thrombozyten als w haben. Aber bei 3 ? So wie ich das sehe sagt der U test bei signifikanz dann nur aus das es zwischen M/W einen unterschied gibt, aber nicht welchen, oder? Welchen test kann ich in diesem Fall nehmen?
Hallo Pas,
die Richtung des Unterschieds siehst du dann daran, in welcher Gruppe du mehr Beobachtungen in den kleinen oder großen Werten hast. Du könntest auch einen Chi-Quadrat-Test für eine Kreuztabelle rechnen.
Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Eine kurze Frage noch über diesen Weg hier, weil es einfacher ist. Also einfach einen U Test oder chi 2 Test rechnen, schauen ob er signifikant ist, und dann manuell gucken, ob m oder w mehr Treffer in den hohen mittleren oder kleinen Ausprägungen hat? Das muss man ja dann manchen egal welchen von den beiden Tests man nimmt, da der chi 2 Test ja auch nur zeigt, dass es einen Unterschied gibt, aber nicht genau wo, oder? Das nächste Problem ist, dass meine beiden Gruppen sehr unterschiedliche Anzahl von Probanden hat. 90 zu 10. dann wird die große Gruppe ja im Prinzip fast überall mehr Treffer haben, weil Sie einfach mehr Probanden beinhaltet, aber prozentual gesehen, eigentlich weniger Treffer hat als die kleine Gruppe. Wie macht man das dann am besten?
Hallo, ja, so ist es richtig. Bei den Kreuztabellen schaust du dir die Prozentwerte pro Gruppe an.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe eine Frage. Ich vergleiche innerhalb einer Gruppe (n=6) die Veränderung von Laborparametern nach Stimulation. Nun kommt beim Wilcoxon-Test für jeden Laborparameter der selbe p-Wert raus (0,0313). Das kommt mir komisch vor. Macht das irgendwie Sinn?
Danke schon einmal im Voraus.
Hallo,
das ist möglich, wenn die Rangfolge immer gleich bleibt. Bei der kleinen Fallzahl kann das durchaus vorkommen.
Für spezielle Fragen – nicht direkt zum Blogbeitrag hier – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
auch von mir tausend Dank fuer Dein Engagement auf Deiner Seite.
Ich habe eine Frage: Nach Applikation eines Medikamentes untersuchten wir diverse Kreislaufparameter nach Sicherstellung Normalverteilung mit dem T Test auf Signifikante Unterschiede-die jedoch nicht vorhanden sind.
Nun meinte ein Kollege, dass eine Normalisierung der Daten die (vorhandenen) Trends der Unterschiedlichkeit verstaerken wuerde und somit statistisch darstellbar.
Meine Fragen:
– Was ist das?
– Wie funktioniert es?
– Gibt es bei uns Sinn, wenn die „handelsuebliche“ Statistik keine Unterschiede darstellen kann?
Vielen Dank im voraus,
Quirin
Hallo Quirin,
für spezielle Fragen – nicht direkt zum Blogbeitrag hier – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Dort tummeln sich viele mit ähnlichen Problemen und auch Antworten dazu und ich schaue auch regelmäßig vorbei.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe Probleme, die Effekstärken dieser Studie zu berechnen. Die Autoren arbeiten hier mit Medianen und dem Wilcoxon-Rangsummentest. Können Sie mir vielleicht weiter helfen, mit welcher Formel man hier rechnen kann?!
Ich hänge Ihnen die Studie einfach mal mit an: http://www.biomedcentral.com/content/pdf/1471-2474-9-105.pdf
Vielen Dank schon mal!!
Beste Grüße
Sandra
Hallo Sandra,
für spezielle Fragen – nicht direkt zum Blogbeitrag hier – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Dort tummeln sich viele mit ähnlichen Problemen und auch Antworten dazu und ich schaue auch regelmäßig vorbei.
Schöne Grüße
Daniela
Hallo Daniela,
danke für diesen tollen Service!
Mitarbeiter werden anonym vor und nach einer Maßnahme zur Zufriedenheit am Arbeitsplatz (Schulnoten 1-6) befragt.
Gelten die Ergebnisse dann als unabhängig? Passender Test für Wirksamkeit der Maßnahme damit der Mann-Whitney oder Wilcoxon oder ganz anderer?
Vielen Dank für die Antwort!
Also konkret lassen sich die Ergebnisse der beiden Befragungen nicht auf die gleiche Person matchen. Damit unabhängig?
Hallo Chris,
Wenn du die Datn nicht mehr zuordnen kannst sind sie somit unabhängig. Bevor du dich dann an Mann-Whitney oder Wilcoxon wagst würde ich erst einmal die ganze deskriptive Statistik durchführen, um Aussagen über deine Daten machen zu können. Anschließend musst du z.B. einen Shapiro-Wilk-Test durchführen um auf Normalverteilung zu überprüfen. Dementsprechend nimmst du dann Mann-Whitney oder T-Test.
Ich hoffe ich konnte deine Fragen beantworten.
Liebe Grüße
Theresa
Hallo Daniela!
Ich benötige einmal deine Hilfe:)
Ich habe einen Versuch mit zwei Stichproben durchgeführt (á n=12).
Das Ziel ist es herauszufinden welche Methode (hier: Trainingsmethode) „effektiver“ ist.
Als H0 wird angenommen, dass sich beide Trainingsgruppen nicht unterscheiden. Jeder Proband wurde an zwei Trainingsstationen gemessen (jeweils Vorher-Nachher Messung).
Ich habe nun von jedem Probanden zwei Werte von zwei Körperregionen (Vorher-Nachher Werte) und weiß nicht welches statistische Verfahren ich verwenden soll.
Meine Idee war es als erstes für jede Gruppe und Körperregion die Werte auf Normalverteilung zu testen. Je nach Verteilung würde ich mit einem unabhängigen T-Test oder eben Mann-Whitney-U-Test fortfahren
Hallo Stefan,
dein geplantes Vorgehen ist richtig: Differenzwerte bilden, dann Normalverteilung prüfen und entweder t-Test oder Mann-Whitney U Test, jeweils für die beiden Körperregionen einzeln.
Schöne Grüße
Daniela
Hallo Daniela,
Ich habe auch eine kurze Frage und zwar zur Auswertung meiner berechneten Ergebnisse.
Ich habe einen nicht verbundenen, nicht normalverteilten Datensatz und auf diesen den kuskal-Wallis Test angewendet.
Ich habe signifikante Unterschiede festgestellt. Teilweise gibt es natürlich auch keine unterschiede aber die Signifikanzen liegen zwischen 0,041- 0,106.(etc. )
Die Frage: kann man die Signifikanzen vergleichen? Also sagen das ein Trend zuerkennen ist bzw. Das ein Wert mehr oder weniger signifikant ist als ein anderer, falls er über 0,05 liegt ?
Lg marius
Hallo Marius,
streng genommen nicht. Aus statistischer Sicht gibt es nur „signifikant“ oder „nicht signifikant“, je nachdem, welches Signifikanzniveau zuvor festgelegt wurde. In der Praxis wird aber oft z.B. zwischen signifikant (<0,05) und hoch signifikant (<0,001) unterschieden. Schöner für den Vergleich von mehreren Unterschiedstests ist es aber, wenn du Effektstärken verwendest (dazu habe ich auch vor kurzem einen Blogbeitrag verfasst).
Schöne Grüße
Daniela
Hallo Daniela!
Erst einmal vielen Dank für die Mühe die Du Dir hier mit der Beantwortung der Fragen machst. Ich finde es super!
Für eine Projektarbeit musste ich 16 Gruppen paarweise auf signifikante Unterschiede testen, also 120 Mann-Whitney-U-Tests durchführen (da die Gruppen nicht normalverteilt sind). Nun habe ich eine Liste von Paaren, die sich signifikant unterscheiden. In Tabellenform habe ich darstellt welche Gruppen sich untereinander unterscheiden. Da es jedoch sehr unübersichtlich ist, habe ich die 16 Konfidenzindervalle der Mediane der einzelnen Gruppen graphisch dargestellt. Jedoch bin ich mir nun nicht sicher, was genau mir diese über die Testergebnisse der Mann-Whitney-U-Tests sagen, bzw. wie ich das Ergebnis anhand der Konfidenzintervalle interpretieren kann.
Über eine Antwort wäre ich sehr dankbar.
Liebe Grüße,
Steffi
Hallo Steffi,
du schaust in der Abbildung, ob sich die Konfidenzintervalle überlappen. Überlappen sich die Konfidenzintervalle von 2 Gruppen nicht, dann hast du wohl auch einen signifikanten Unterschied im Test.
Schöne Grüße
Daniela
Hallo Daniela,
ich führe gerade einen Mann-Whitney-Test durch. Hierfür habe ich 2 Ordinalskalen mit n = 34 und n = 40. Die Daten sind Bewertungen eines Akzents, quasi wie Schulnoten 1 – 5. Als Mittelwert der Ergebnisse möchte ich den Median für gehäufte Daten nehmen. Wo liegt der Vorteil bei einem Median für gehäufte Daten gegenüber eines arithmetischen Mittels? Ist der Median aussagekräftiger? Die Daten sind zwar ordinalskaliert, aber dennoch habe ich nunmal die Zahlen 1 – 5.
Danke für deine Hilfe!
Hallo Philip,
der Median ist bei ordinalen Daten besser, weil er die Skalenart besser berücksichtigt. Beim arithmetischen Mittel geht man eigentlich davon aus, dass die Abstände zwischen den Messpunkten gleich sind („gleichabständige Skala“ = metrisch). Das ist bei Ordinaldaten streng genommen nicht der Fall. Trotzdem wird das arithmetische Mittel auch hier häufig eingesetzt und hat sich auch bewährt.
Schöne Grüße
Daniela
Liebe Daniela,
zunächst möchte auch ich dir danken für die Unterstützung die du anbietest.
Ich würde gerne auf deine Hilfe zurückgreifen, da ich im Moment selber nicht weiter komme.
Ich untersuche einen Einzelfall hinsichtlich Beeinträchtigungen in der Theory of Mind (ToM) und anderer neuropsychologischer Funktionsbeeinträchtigungen nach einer Hirnschädigung. Da es bei den ToM Testverfahren noch keine Normierungsstudien gibt, habe ich eine kleine Kontrollstichprobe erhoben, mit denen ich den Patienten in unterschiedlichen Tests der ToM vergleichen will. Die Testergebnisse sind in der Kontrollgruppe jedoch nicht normalverteilt sondern rechtsschief (es wurden eher höhere bis maximale Punktwerte erzielt). Nun möchte ich herausfinden, ob der Patient im Vergleich zu den Kontrollprobanden schlechtere Ergebnisse zeigt. Mein Prof. meinte, ich solle einfach den z-Wert des Patienten ermitteln… Da ich dies jedoch als bei der vorhersschenden Verteilungslage der Daten nicht gewährleistet sehe, suche ich nun nach einer anderen Möglichkeit. Ich ziehe den Mann-Whitney-U-Test in Erwägung, weiß aber nicht, ob dieser bei einer Stichprobengröße von 1 (im Falle der „Patientengruppe“) angwendet werden kann oder brauchbare Ergebnisse liefert.
Kannst du mir diesbezüglich weiterhelfen?
Ich bin dankbar über jede Hilfestellung und freue mich sehr auf deine Antwort.
Viele Grüße
Lisa
Hallo Daniela,
ich benötige deine Hilfe, ich verzweifle hier schon. Und Zwar suche ich eine statistische Testmethode oder irgend ein Hinweis was zu tun ist. Ich will nachweisen das die Messergebnisse, die aus zwei unterschiedlichen Messgeräten stammen, gleichwertig sind (also gleiche Messergebnisse liefern). Denn es das eine Messgerät soll das andere ersetzen, aber nur wenn die Messergebnisse die gleichen sind. Mein Plan ist: Vergleichsversuche durchführen. Dabei werden die gleichen Bedingungen und Objekte genutzt. Aus Kosten- und Zeitgründen werden je Messgerät 6 Versuche durchgeführt. Nun will ich die Messergebisse vergleichen, wie kann ich das machen? Nutze ich die deskriptive oder induktive Statistik? Oder ist die Zuhilfenahme von Statistik überhaupt Sinnvoll?
Mit freundlichen Grüßen
David Glowania
Hallo David,
du könntest mit Konfidenzintervallen arbeiten. Wenn das Konfidenzintervalls des Unterschieds zwischen den beiden Gruppen die 0 einschließt, unterscheiden sie sich nicht deutlich. Allerdings ist das mit nur 6 Versuchen eventuell problematisch, da die Konfidenzintervalle bei kleinen Fallzahlen automatisch groß ausfallen, also ganz leicht schon die 0 einschließen. Außerdem ist es wichtig für die Interpretation zu wissen, welche Abweichung für dich noch „keine Abweichung“ wäre.
Schöne Grüße
Daniela
Danke Daniela für deine Antwort,
ich habe gedacht, dass ich eine Hypothese aufstelle und diese dann annehme und das mit dem doppelten t-test Beweise. Aber ich glaube es ist Sinnvoller es mit ein einem Konfidenzintervall zu beweisen.
Schöne Grüße
David
Hallo Daniela,
ich habe ein größeres Problem und weiß nicht wie ich es angehen kann.
Ich möchte die Veränderungen in den Daten, die in 2 verschiedenen Jahren erhoben wurden (2013 vs. 2014), auf Signifikanz prüfen. Die Daten stammen nicht von gleichen Personen, nur dem gleichen Personenkreis.
Nun habe ich verschieden skalierte Daten im Fragebogen, meistens nominalskaliert, z.B. würden Sie das Produkt empfehlen: ja/nein, aber auch eine Frage die auf einer Skala von 1-8 beantwortet wurde.
Erfasst werden soll die Wirksamkeit eines Werbespots – wonach auch die Gruppen aufgeteilt werden sollen, also Werbespot gesehen: ja/nein – und es geht also um die Auswirkungen des Spots auf die verschiedenen Bewertungen des Produkts.
Ich würde mich sehr über eine Antwort freuen die mir beim weiteren Vorgehen hilft.
Lieber Gruß
Alexander
Hallo Alexander,
zunächst ist es notwendig, dass du deine Fragestellungen und die passenden Hypothesen dazu genau formulierst. Dann kann man an die Testauswahl gehen. Kennst du mein E-Book (https://statistik-und-beratung.de/gratis-e-book-statistische-datenanalyse-die-grundlagen/)? Das gibt einen Überblick über diese ersten Schritte und die Basic-Methoden zum Starten.
Schöne Grüße
Daniela
Liebe Daniela,
um entscheiden zu können, welchen Test ich für den statistischen Vergleich durchführen muss, habe ich mithilfe des von Dir empfohlenen QQ-Plots auf Normalverteilung geprüft. Mich hat hierbei aber die Beobachtung verunsichert, dass meine x- und y-Achse im -1 Bereich beginnen.
1) Ist das normal? Und wenn ja, woran liegt das?
Darüber hinaus bin ich auch bei folgenden Aspekten noch etwas unsicher:
2) Für welche Gruppen werden der Levene- und der t-Test durchgeführt? Nur für die Gruppe, auf die ich mich in den Analysen fokussiere (also z.B ttest polit. Einstellung, by(geschlecht)) oder auch für die anderen unabhängigen Variablen, die ich zusätzlich verwende (z.B. ttest polit. Einstellung, by(migration)) ?
3) Welchen Test muss ich bei zwei metrischen Variablen durchführen? Der t-Test funktioniert bei AV und UV metrisch ja nicht.
4) Wird der Chi-Quadrat Test nur die die unabhängigen Variablen oder auch für die Kontrollvariablen ausgeführt?
5) Wenn in die Regression das quadrierte Alter hinzugefügt wird, wie ist dessen Koeffizient von -.0007131 zu interpretieren? Und was muss ich bei der Interpretation der Konstanten dann beachten?
Besten Dank im Voraus und schöne Grüße
Hallo Eleo,
1) ja, das ist normal. Hier werden die Quantile angetragen, nicht die Werte an sich.
2) Levene und t-Test werden immer für die Gruppenvariable berechnet, die du gerade analysierst. Wenn du für unterschiedliche Gruppierungen t-Tests durchführst, machst du Levene und t-Test für jede einzeln.
3) was hast du mit den beiden metrischen Variablen vor? Zusammenhänge aufdecken? Dann wäre das eine Korrelation.
4) den Chi-Quadrat-Test nimmst du immer, wenn du den Zusammenhang zwischen zwei kategorialen Variablen untersuchen willst.
5) Wenn das quadrierte Alter um eine Einheit ansteigt, fällt die abhängige Variable um .0007131 ab.
Schöne Grüße
Daniela
Hallo Daniela,
ich würde mich sehr freuen, wenn du mir bei zwei statistischen Fragen helfen könntest.
Ich untersuche in meiner Masterarbeit Unterschiede in Bezug auf Generation X und Y.
Dabei habe ich Führungseigenschaften als Mehrfachantwortenset in meiner Arbeit erhoben und nominal skaliert.
Nun möchte ich überprüfen, ob diese Eigenschaften sich hinsichtlich Generation X und Y unterscheiden. Ich habe hierfür eine Chi2 test mit Kreuztabellen vorgenommen, bin mir allerdings nicht sicher da Generationen eine Ordinate Variable ist?
Des Weiteren möchte ich nun diese Eigenschaften hinsichtlich Job Positionen (5 Positionen) auch nominal skaliert testen. Welchen Test wende ich hierfür an? Bei vielen Feldern ist die Vorraussetzng für Chi2 mit 5 Faktoren leider nicht gegeben.
Beste Grüße,
Karina
Hallo Karina,
für die Führungseigenschaften (Mehrfachantworten) brauchst du für jede Eigenschaft einzeln eine Variable (Eigenschaft ja/nein), die du zusammen mit der Variablen Generation (X/Y) mit einer Kreuztabelle und dem Fishers Exakten Test analysieren kannst. Chi-Quadrat ist auch möglich, aber da das eine 2×2 Tabelle ist, ist Fisher besser.
Beim Zusammenhang zwischen Führungseigenschaften (wieder jede einzeln als Ja/nein) und 5 Job Positionen passt eine Kreuztabelle mit Chi-Quadrat Test, genau. Wenn es Zellen mit zu wenigen Beobachtungen gibt, solltest du versuchen, die 5 Job Positionen in weniger Kategorien zusammen zu fassen.
Schöne Grüße
Daniela
Hallo Daniela,
deine Seite ist wirklich sehr hilfreich. Danke für die vielen Erklärungen.
Ich habe eine spezifische Frage zu meiner Studie und würde mich über eine Antwort sehr freuen.
Ich habe die Motorik von Schülern mittels 8 Testaufgaben vor und nach einem Sportprogramm getestet und hatte dafür eine Versuchsgruppe (15 Probanden) und eine Kontrollgruppe (16 Probanden). Bei beiden Gruppen sind die Leistungen in den Tests nach dem K-S-Test mehr oder weniger normalverteilt und daraufhin habe ich bei beiden den T-Test für abh. Stichproben angewandt. Die Versuchsgruppe hat sich bei 3 Testaufgaben signifikant verbessert und die Kontrollgruppe bei einer Testaufgabe. Somit hat das Sportprogramm die Motorik in manchen Bereichen positiv verändert. Wenn ich allerdings die Veruchs- und die Kontrollgruppe miteinander vergleiche, kann zu beiden Testzeitpunkten bei allen 8 Testaufgaben kein signifikanter Unterschied festgestellt werden. Also sind die Leistungen der beiden Gruppen vorher ungefähr gleich und nach dem Sportprogramm auch, obwohl innerhalb der Gruppen ein signifikanter Unterschied festgestellt werden kann. Kann es sein, dass ich falsch vorgegangen bin oder wie kann ich dieses Ergebnis interpretieren? Wird die Aussage der Verbesserungen dadurch geschwächt?
Über eine Antwort wäre ich sehr dankbar.
Viele Grüße
Daniel
Die beiden Gruppen habe ich bei beiden Testzeitpunkten mit dem T-Test für unabhängige Stichproben getestet.
Hallo Daniel,
bei diesem Studienaufbau würde ich die Differenzen untersuchen und nicht die erhobenen Werte an sich. Du rechnest also für jeden Teilnehmer für jede Aufgaben den Differenzwert „Nachher minus vorher“ aus. Dann kannst du anschließend diese Differenzwerte zwischen den beiden Gruppen (Versuch und Kontrolle) mittels t-Test für unabhängige Stichproben vergleichen. Damit bekommst du heraus, ob es eine unterschiedliche Änderung zwischen den beiden Gruppen gibt. Das müsste genau deine Fragestellung beantworten, oder?
Schöne Grüße
Daniela
Hallo Daniela,
danke für die Antwort. Ja, dieser Gedanke ist mir mittlerweile auch schon gekommen, ich war mir aber unsicher, ob das einfach so möglich ist. Das trägt dann auf jeden Fall zu meiner Sicherheit bei. 🙂
Ich bin aber noch auf ein weiteres mögliches Verfahren gestoßen: die (split-plot?) Varianzanalyse mit Messwiederholung, bei der dann der Interaktionseffekt berechnet wird und ich dadurch ja Aussagen über die Wirkung des Programms machen könnte. Sollte ich lieber bei dem unabhängigen T-Test bleiben oder wäre es auch sinnvoll erst den abhängigen T-Test durchzufüren, um zu sehen ob Unterschiede in den Gruppen auftreten und dann mit der Varianzanalyse prüfen ob auch Unterschiede zwischen den Gruppen vorhanden sind?
Vielen Dank im Voraus und liebe Grüße
Daniel
Hallo Daniel,
ja genau, du kannst genausogut eine zweifaktorielle ANOVA rechnen (ein Faktor Zeit, ein Faktor Gruppe) und die Interaktion betrachten. Ist die signifikant, ändern sich die Gruppen unterschiedlich. Das ist genau das, was du zeigen willst. Die Methode ist genauso in Ordnung wie die Verwendung der Differenzen und dann einen einfachen Gruppenvergleich.
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für deine Antwort!
Dann werde ich das so durchführen für den Vergleich. Um die Veränderung innerhalb der beiden Gruppen besser zu beurteilen, nehme ich dann den T-test für abh. Stichproben und für den Unterschied zwischen den Gruppen die zweifaktorielle Varianzanalyse mit Messwiederholung.
Liebe Grüße
Daniel
Hallo Daniela,
ich würde mich sehr freuen wenn du mir bei einer Statistik-Frage weiterhelfen könntest.
Ich habe eine Experimentalgruppe die vor dem Treatment bezüglich mehrerer AV’S (metrisch) gemessen wird und eine Woche nach dem Treatment. Dasselbe gilt für die Kontrollgruppe, die jedoch kein Treatment erhält. Meine Experimentalgruppe kann aber noch in 5 verschiedene Subgruppen unterteilt werden und ich würde gerne herausfinden, ob bestimmte Subgruppen „mehr“ vom Treatment beeinflusst werden, als andere. Hast du einen Tipp wie man bei SPSS vorgehen kann? Das wär klasse
Herzliche Grüße
Hallo Marie,
hier würde ich erstmal Differenzen bilden (Nachher minus Vorher) und diese Differenzen dann als abhängige Variable verwenden (die beschreiben dann die Änderung).
Dann könntest diese Differenzwerte für jede Subgruppe mit der Kontrollgruppe vergleichen (bei Normalverteilung mit t-Test, ansonsten mit Mann-Whitney U). Durch die Tests bekommst du heraus, ob der Unterschied signifikant ist oder nicht. Zusätzlich würde ich für jeden Paarvergleich die Effektstärke berechnen (beim t-Test mit Cohens d, beim Mann-Whitney U mit der Effektstärke z/wurzel(n), z ist dabei die Teststatistik des Mann-Whitney U Tests, n die Fallzahl). Diese gibt dir an, wie groß der Unterschied zwischen Subgruppe und Kontrolle ist. Dadurch siehst du, bei welcher Subgruppe der Effekt am größten ist, bei welcher am zweitgrößten usw.
Schöne Grüße
Daniela
Hallo Daniela,
ich finde es super, wie du hier weiterhilfst und hoffe, du kannst mir auch weiterhelfen 🙂
vorab: ich bin noch ein Frischling in SPSS :/! Ich habe 2 Variablen (welche Kompetenzen man beherrscht und welche von einem gefordert werden). Welcher test würde da am besten in Frage kommen, um diese miteinanderzuvergleichen? Mittelwertvergleich? Aber was wäre dann meine Gruppenvariable? Einfach alle, die als Beruf Jurist angegeben haben? Um die geht es nämlich!
Ich würde mich riesig über eine Antwort freuen )
Liebe Grüße
Ric
Hallo Ric,
wie genau sind das Beherrschen und die Forderung der Kompetenzen gemessen? Als Kategorien (ja/nein) oder auf einer Skala (z.B. Einschätzung 1 bis 10)?
Wenn es Kategorien sind, passt wohl eine Kreuztabelle und ein Chi-Quadrat-Test oder Fishers Exakter Test. Der Test gibt dann an, ob es einen signifikanten Zusammenhang zwischen den beiden (Beherrschen und Forderung) gibt.
Wenn sie auf einer (und zwar der gleichen) Skala gemessen sind, ginge ein Mittelwertsunterschied zwischen Beherrschen und Forderung (Unterscheiden sich die beiden signifikant). Das wäre dann bei Normalverteilung ein gepaarter t-TEst, ansonsten der Wilcoxon-Test.
Bei diesen Daten ginge außerdem eine Korrelation, um den Zusammenhang zwischen den beiden zu untersuchen (bei Normalverteilung Pearson, ansonsten Spearman).
Hol dir doch mein kostenloses E-Book, da steht das alles drin 🙂
Schöne Grüße
Daniela
Liebe Frau Keller,
ich habe eine Frage zur Erstellung einer Grafik.
Falls Sie mir helfen könnten, wäre das wunderbar, ich kriegs einfach nicht hin…
Also: Ich möchte zwei Gruppen in ihrer Leistung vergleichen. Links soll das Diagramm der Gruppe A sein, rechts zum Vergleichen das Diagramm Gruppe B. Die y-Achse soll die Mittelwerte der Variablen darstellen. Die x-Achse, und das ist das Problem, die drei Messzeitpunkte. Es soll die Entwicklung von 5 Variablen veranschaulicht werden. Also die Mittelwerte zum 1., 2. und 3. Messzeitpunkt jeweils als Linie, sodass bei Gruppe A 5 Linien verlaufen und bei Gruppe B im Diagramm auch.
Ich hoffe, ich konnte es einigermaßen erklären…
Vielleicht nicht ganz unwichtig: Die Variablen haben leider nicht die gleiche Skala. Muss ich sie deshalb erst alle z-standardisieren? (Vielleicht ist das auch eine dämliche Frage…) 😉
Viele Grüße
Anna
Hallo Anna,
zur zweiten Frage (Standardisierung): Soll denn die Skala noch ablesbar sein? Dann nicht standardisieren und stattdessen mehrere Skalen (y-Achse) einfügen (das wird wohl ziemlich unübersichtlich). Wenn die Skala nicht mehr interpretiert werden soll, dann eventuell mit standardisierten Werten arbeiten.
Zur Umsetzung an sich: Mit welcher Software hattest du das vor? Ich befürchte, in SPSS geht das nicht. Ich würde die Mittelwerte in einer Excel-Tabelle eintragen und dort so ein Diagramm bauen. Das wird ein bisschen Handarbeit…
Schöne Grüße
Daniela
Hey Daniela,
ich hätte mal eine Frage und zwar habe ich 2 Gruppen (Normale Gruppe und Kontrollgruppe) und möchte die Vergleichen! Da muss ich jetzt einen T-Test für unabhängige Stichproben nehmen, oder? Die Testvariable, hat in meinem Fall 3 Ausprägungen und zwar 0=nein, 1=mit positivem Verlauf, 2=mit negativem Verlauf! Wie muss ich das jetzt machen wenn ich für jede der Ausprägungen einen extra T-Test machen möchte oder ist dies überhaupt sinnvoll?
Beste Grüße und vielen Dank
Katja
Hallo Katja,
die Testwariable ist mit 0,1 und 2 kategorial und nicht metrisch. Deshalb passt hier nicht der t-Test sondern eine Kreuztabelle mit Chi-Quadrat-Test.
Schöne Grüße
Daniela
Hallo Daniela,
Ich hätte eine Frage, die mich seit langem umtreibt: im Zuge einer klinischen Studie habe ich zwischen verschiedenen Gruppen Differenzen berechnet, die sowohl positiv, als auch negativ ausfallen. In einigen Fällen schwanken die Werte um 0, sodass der Mittelwert bei 0 liegt. Wäre es in diesem Fällen deiner Meinung nach sinnvoll mit absoluten also immer positiven Zahlen zu arbeiten?
Schöne Grüße und besten Dank vorweg
Imanuel
Hallo Imanuel,
das kommt darauf an, ob dich die Richtung des Unterschieds interessiert oder nicht. Wenn die Richtung interessiert, müssen die Werte so bleiben. Wenn die Richtung egal ist und es nur um die Abweichung geht, kannst du den Betrag der Werte nehmen.
Schöne Grüße
Daniela
Hallo Daniela,
ich bitte dich um Unterstützung bei folgender Frage:
Ich möchte eine Fallzahlplanung für die benötigte Stichprobengröße berechnen, für einen Fragebogen mit Ordinal- und Nominalskala, Vergleich von 2 Gruppen (Unterschied)
primär wollte ich diese mit dem T-Test durchführen (wie auf der Homepage beschrieben), doch dieser ist doch für Intervallskala? Mit welchem Test könnte ich das mit G*Power machen und was müsste ich da eingeben?
DANKE und liebe Grüße,
Helga
Hallo Helga,
beim Vergleich von 2 Gruppen mit Ordinalskala nimmst du den Mann-Whitney U Test. Den gibt es auch in G*Power zur Auswahl, um die benötigte Fallzahl zu ermitteln.
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für die tolle Unterstützung, die Du hier bietest!
Ich möchte zwei Testverfahren, die ich mit den gleichen Personen durchgeführt habe miteinander vergleichen. Die Daten eines Testverfahrens sind nicht normalverteilt. Nun meine Fragen:
1. Beschreibe ich nun grundsätzlich den Median oder den Mittelwert? Bei einem Testverfahren habe ich einen deutlichen Bodeneffekt, beim anderen 3 Extremwerte (N = 70) ?
2. Es handelt sich doch um eine verbundene Stichprobe, oder? D.h. ich verwende den Wilcoxon?
3. Wie überprüfe ich eigentlich, ob ein Extremwert relevant ist?
4. Ich habe noch einige andere Variablen und möchte weiterhin überprüfen, ob es je nach Testverfahren unterschiedliche Zusammenhänge zu diesen Variablen gibt. Welche Verfahren wende ich an?
Schon mal vielen Dank für deine Antwort!
Andrea
Hallo Andrea,
zu 1) laut deiner Beschreibung würde ich eher zum Median tendieren. Auch bei normalverteilten Daten passt der gut, weil er dann nahe am Mittelwert liegt.
zu 2) Ja.
zu 3) Ist er denn für dich relevant? Ist er unrealistisch weit weg? Wenn du nichtparametrische Verfahren benutzt (z.B. Wilcoxon), stört er die Ergebnisse nicht. Dann kann er aus statistischer Sicht einfach drin bleiben.
zu 4) kommt auf das Messniveau dieser anderen Variablen an: nominal, ordinal, metrisch? Wenn du dir mein kostenloses E-Book holst, findest du da alles drin 🙂
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für die klaren Antworten. Jetzt arbeite ich mit ruhigerem Gefühl weiter! Und das E-Book habe ich mir natürlich geholt:-).
Schöne Grüße,
Andrea
Jetzt habe ich doch noch einmal eine Frage zur Relevanz der Ausreißer. Hinsichtlich der Frage nach dem Unterschied in beiden Testverfahren spielen die Extremwerte keine Rolle. Wenn ich habe die Zusammenhänge mit anderen Variablen untersuche und dies noch in Abhängigkeit vom Ergebnis in beiden Testverfahren (auffällig ja/nein), dann bekomme ich doch sehr unterschiedlich Ergebnisse (je nachdem, ob ich mit oder ohne Ausreißer auswerte). Also, d.h., nehme ich die gesamte Stichprobe und untersuch die Zusammenhänge zwischen den beiden Testverfahren und den weiteren Variablen, dann bleiben die Korrelationskoeffizienten (Spearman) etwa gleich hoch und gleich signifikant, egal ob mit oder ohne Ausreißer (in einem Fall N=70, im anderen Fall N=62). Teile ich meine Daten auf, je nachdem, ob beide Testverfahren auffällig oder unauffällig waren, dann bekomme ich dort ganz andere Korrelationskoeffizienten mit entsprechend anderen Signifikanzen (die Gruppengröße ändert sich von 27 auf 24 bei der unauffälligen Gruppe und von 22 auf 17 bei der auffälligen). Grundsätzlich sind die Extremverwerte keine Messfehler und auch nicht unrealistisch weit weg, sondern eher unter „individuelle Varianz in psychometrischen Testverfahren“ zu verbuchen.
Weiß jetzt nicht so recht, wie ich damit umgehen soll. Kann ich, da ich ja auch bei den Korrelationen nicht-parametrische Verfahren verwende, diese Extremwerte ignorieren, wie letztlich beim Wilcoxon auch?
Sorry, dass der Text so lang wurde, aber so ist es vielleicht verständlicher.
Danke für Deine Antwort und schöne Grüße,
Andrea
Hallo Andrea,
wenn du keine Begründung hast, um die Ausreißer heraus zu nehmen (und da es ja doch einige sind, bei deiner Stichprobe), würde ich sie nicht heraus nehmen.
Und ja: bei den nichtparametrischen Verfahren (Spearman) sind die Ausreißer egal. Spearman benutzt die Ränge, nicht die eigentlichen Messwerte. Deshalb „merkt“ er nicht einmal, dass die Werte weit weg sind. Für ihn sind es einfach nur die größten.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe zwei unverbundene Gruppen (n=19; n=150). Die Stichproben sind nicht normalverteilt. Kann ich den Mann-Whitney-U-Test sinnvoll durchführen oder brauche ich einen anderen Test aufgrund der so unterschiedlichen Stichprobengrößen?
Vielen Dank im Voraus für deine Hilfe!
Beste Grüße
Hallo,
die unterschiedlich großen Stichproben sind kein Problem für den Mann-Whitney U. Eventuell hat er aufgrund der einen kleinen Stichprobe keine sehr hohe Power, kann also den Unterschied eventuell nicht als signifikant nachweisen. Aber erlaubt ist er und ich wüsste auch keine Alternative mit einer höheren Power.
Schöne Grüße
Daniela
Hallo Daniela, ich habe auch eine Frage an dich: Ich wende einen Related-Samples Wilcoxon an, weil ich schauen möchte ob Schüler nachher interessierter sind als vorher. Dieses Interesse mit einer Skala berechnet, die aus mehreren Fragen besteht. Das Ergebnis für jeden Schüler, das dann in den Wilcoxon einfließt, kann ich entweder mit mean oder median berechnen. Das ist meine Frage. Welche Grundlage sollte ich nehmen? Da die Daten sich ja als nicht normalverteilt herausstellen (mit dem mean als Grundlage), sollte ich vielleicht hier den median nehmen?
Danke!!
Hallo,
ja, dann passt der Median besser.
Schöne Grüße
Daniela
Hallo, ich wäre Ihnen sehr dankbar, für die Hilfe bei folgender Fragestellung.
Ich habe 3 Gruppen (Op1, Op2, keine Op) zu 3 verschiedenen Zeitpunkten verglichen. Jetzt möchte ich den Faktor Schmerz (1-100Punkte) im longitudinalen Vergleich betrachten. Ich möchte aber nicht die 3 Opverfahren innerhalb eines Zeitpunktes vergleichen, sondern will statistisch darlegen, dass der Schmerz im Verlauf bei OP 1 beispielsweise nach 1 Tag mehr anstieg als bei OP 2, aber dann an Tag 2 gleichbleibend war.
Ich hoffe meine Frage ist verständlich!
Beste Grüße
Hallo Linda,
das klingt nach einer Mixed Design ANOVA (zweifaktorielle ANOVA mit einem Messwiederholungsfaktor und einem Gruppenfaktor). Was du da sehen willst ist eine signifikante Interaktion zwischen den beiden Faktoren.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe in einer einmaligen Erhebung über 100 Personen befragt, u.a. zu Einstellungen. Dafür verwendet wurde eine 4-stufige Skala. Jetzt habe ich Gruppen gebildet durch Dichotomisierung (lehne ich komplett ab & lehne ich eher ab vs. stimme ich eher zu & stimme ich vollkommen zu). Die Gruppengrößen sind je Einstellungsfrage unterschiedlich und die Auswertungen beziehen sich jeweils auf eine erfragte Einstellung – eine Kombination oder Skalenbildung ist wenig sinnvoll, da es sich um unterschiedliche, jeweils eigenständige Themenbereiche je Einstellungsfrage handelt.
Kann ich hier irgendwelche sinnvollen Gruppenvergleiche außerhalb von deskriptiven Analysen machen?
Vielen Dank im Voraus & viele Grüße,
Sonja
Hallo Sonja,
du bekommst die Gruppenbildung aus den gleichen Variablen, die die du dann vergleichen willst? Dann macht ein Signifikanztest für einen Gruppenvergleich keinen Sinn.
Gruß
Daniela
Sehr geehrte Frau Keller,
ich habe eine klinische Studie durchgeführt. Nun habe ich mehrere Messwerte für die Patienten von 2009 bis 2014. Ich möchte dieses zeitlichen Verlauf mit Boxplots für 2 unterschiedliche Gruppen darstellen. Auf der y-Achse sollten die Messwerte stehen und auf der x-Achse die Messzeitpunkte. Nun habe ich in meiner SPSS Tabelle die Variable Messzeitpunkte noch nicht. Bei Excel ist das leicht man markiert nur den Datenbereich. Allerdings habe ich dort kein guten Gefühl bezüglich der Berechnung der Boxplots ich hätte es gerne in SPSS. Ich bin aber etwas verloren da meine Variablen die Messwerte sind und meine Gruppen definiert sind. Mir fehlt die Kategorieachse und ich weiß nicht wie ich eben SPSS diese Variable „Messzeitpunkte“ klar mache. Etwas Chaos ich weiß aber besser kann ich es nicht erklären …..Vielen Dank!
Hallo Caroline,
hast du die Messwiederholungen als einzelne Spalten in den Daten? Und die Gruppen sind über eine eigene Gruppierungsvariable definiert?
Dann bekommst du diesen Boxolot über Analysieren -> Deskriptive Statistik -> Explorative Datenanalyse. Gibst da die Messwiederholungen als abhängige Variablen und die Gruppierungsvariable ins Feld Faktorenliste ein. Gehst auf Diagramme und aktivierst dort „Boxplot: Abhängige Variablen zusammen“. Dann müsste das klappen. Über das Diagramm-Menü geht dieser Boxplot nicht.
Schöne Grüße
Daniela
Liebe Frau Keller,
vielen Dank für Ihre Antwort. Ich habe das Problem auch in die FB geschrieben mit einer Graphik dann wird es deutlicher. Ich werde das mal probieren. Das Problem ist nur weiterhin dass ich ja die Messzeitpunkte in Jahren auf der x-Achse haben will und die Boxplots sollen die Messwerte darstellen. Die Messwerte sind einzelne Spalten und die Gruppen haben ich über eine Gruppenvariable definiert. Aber wie sage ich SPSS das es an Messzeitpunkt 0 die Werte aus Gruppe 1 und Gruppe 2 nebeneinander darstellt……diese Definition dieser Variablen treibt mich um….oder ich habe einen Knick im Kopf….
Hallo Caroline,
wenn die Daten so aufgebaut sind, funktioniert das genau so wie ich es geschrieben haben in SPSS. Der „Normale“ Weg über die Diagrammerstellung geht dann nicht. Probiers mal aus und melde dich, ob es geklappt hat!
Daniela
Das mache ich. DANKE! 🙂
und noch was!
Ich habe über 300 Probanden. Aufgrund dieser höhen Fallzahl ist es nicht möglich einfach den gepaarten t-Test zu nehmen?
Danke im Voraus
sara
Ja, bei einer so großen Stichprobe reagiert der gepaarte t-Test wohl signifikant auf die Abweichung von der Normalverteilung. Der wäre also auch möglich.
Nochmal vielen herzlichen Dank für die ausführliche Antwort 🙂
Weiterführende Fragen könnt ihr gern mit mir und den anderen Teilnehmern in der Facebook-Gruppe Statistikfragen diskutieren. Hier der Link: https://www.facebook.com/groups/785900308158525/
Hallo Frau Keller
erstmal muss ich sagen dass ich Ihre Webseite und Ihre Hilfsbereitschaft toll finde und Ihnen dafür sehr dankbar bin.
Ich habe zwei likertskalierte (7 stufig) Variablen, genauer gesagt Zufriedenheit mit X und Zufriedenheit mit Y. Die sind von der selben Stichproben erhoben. Ich möchte wissen ob es eine Unterschied zwischen Zufriedenheit mit X und Zufriedenheit mit Y gibt.
Ich habe einmal den Wilcoxon Test benutzt (mit nicht signifikantem Ergebnis). Dann habe ich den Chi-quadrat Test genommen um zu gucken ob die Verteilungen gleich sind aber habe komische Weise ein signifikantes Ergebnis erhalten. Die Unterschiede zwischen p-Werte sind gewaltig.
diese Unterschiede Ergebnisse irritieren mich so dass ich nicht weis welche ich nehmen soll! Ich habe eigentlich immer gedacht bei so einer Situation die beiden Tests äquivalent funktionieren.
Ich werde mich auf Ihre Antwort freuen.
Beste Grüße,
Sara
Hallo Sara, Wilcoxon prüft die beiden Messungen auf einen Unterschied in der Lage. Der war scheinbar nicht deutlich genug, um bei der Stichprobengröße signifikant zu sein. Der Chi-Quadrat-Test untersucht, ob sich die Verteilungen unterscheiden (nicht nur, ob sich die Lage unterscheidet). Scheinbar gibt es hier einen deutlichen Unterschied in der Verteilung, der sich aber nicht insgesamt in einer unterschiedlichen Lage widerspiegelt. Beim Chi-Quadrat-Test musst du außerdem beachten, dass mindestens 5 Beobachtungen in jeder Zelle liegen sollten, damit das Ergebnis verlässlich ist!
Vielen vielen Dank für die Antwort. Nun frage ich mich welchen Test soll ich in meiner Arbeit anbringen? Der Lage-test oder der Verteilung-test? Was ist Ihre Meinung?
Die Fragestellung lautet: gibt es Unterschied zwischen Zufriedenheit mit X und Zufriedenheit mit Y.
Beste Grüße
Wenn du auf Unterschied testest, dann ist das der Wilcoxon.
Sehr geehrte Frau Keller,
Ihre Antwort ist nicht ganz richtig — leider.
Nicht die Anzahl der Beobachtungen soll größer gleich 5 sein, sondern die erwarteten Häufigkeiten müssen dies erfüllen. Und dann auch nicht in allen Zellen, sondern in mind. 80 Prozent aller Zellen. So sagt es der Kollege Cochran (ich glaube schon im Jahr 1953)
Nichts für ungut
R. Ostermann
Da haben Sie recht, danke!
Schöne Grüße
Daniela Keller
Hallo Daniela
Für meine Bachelorarbeit hab in einem Experiment u.a. gemessen, ob und inwiefern sich die Kaufhäufigkeit von zwei bekannten Smartphones in zwei Conditions unterscheidet (Condition 1: bekannte Smartphones nebeneinander; Condition 2: bekannte Smartphones in der grösstmöglichen Distanz) auf einem virtuellen Regal mit weniger bekannten Smartphones platziere. Nun bin ich mir nicht sicher, welchen Test ich für die Überprüfung möglicher Unterschiede in der Kaufhäufigkeit anwenden muss (die Variable „Condition“ ist nominalskaliert, die Variable für den Smartphonekauf wurde so gemessen, dass sich jeder Proband für ein von 12 Smartphones entscheiden konnte >Wenn ich jetzt die Kaufhäufigkeit für bekannte und weniger bekannte Produkte in den beiden Conditions (also 2 Faktoren pro Condition) vergleichen will, wie ist diese Variabel dann skaliert?) > Ich tendiere eigentlich zu einem Mann-Whitney-U-Test, aber die Variable „kaufsmartphone“ ist doch nominalskaliert?
Hallo, du hast von jedem Teilnehmer die Variable Condition mit Ausprägungen nebeneinander/Distanz und die Variable Kauf mit Ausprägungen bekannt/unbekannt, oder? Dann sind das zwei nominalen Variablen mit jeweils zwei Ausprägungen und das ist Fishers Exakter Test. Siehe auch mein E-Book: https://statistik-und-beratung.de/gratis-e-book-statistische-datenanalyse-die-grundlagen/
Liebe Daniela,
Ich habe im Rahmen meiner Bachelorarbeit einen Datensatz erstellt. Da ich nun keine besonders guten Ergebnisse bekommen habe (Hypothese nicht bestätigt) würde ich gerne einen Vergleich der Ergebnisse meiner Studie mit den Ergebnissen einer anderen durchführen. Nun liegen mir der Mittelwert, die Standardabweichung und die Teilnehmerzahl der anderen Studie vor, nicht aber der gesamte Datensatz. Kann ich mittels SPSS dennoch einen Vergleich durchführen? Wenn ja wie genau funktioniert das. (Nicht alle Variablen sind normalverteilt! Es müssen also für unterschiedliche Variablen unterschiedliche Tests genommen werden) (alle Variablen sind intervallskalliert) (es handelt sich um unabhänige Variablen, also NICHT gepaart)
Vielen Dank schonmal im Voraus (ich hoffe die Frage wurde nicht schon gestellt und ich habe sie überlesen..)
Liebe Grüße, Pete
Hallo Pete, mit den Mittelwerten, Standardabweichungen und Fallzahlen kannst du entweder parametrische Tests „von Hand“ ausrechnen (z.B. für den t-Test, die Formel für die Teststatistik verwenden und dann über Tabellen den p-Wert heraussuchen) oder du berechnest die Konfidenzintervalle und vergleichst die (für deine Daten bekommst du die von SPSS, mit den Zahlen aus den anderen Studien kannst du sie auch mit ner Formel ausrechnen). Dafür müssten die Daten aber immer annähernd normalverteilt sein, oder die Fallzahl groß, so dass die Methoden robust werden. Mit nicht-normalverteilten Daten nur von Mittelwerten und Standardabweichungen ausgehend zu rechnen ist schwierig.
Danke! 🙂
Ich werds mal ausprobieren.
Sehr geehrte Frau Keller,
zunächst ein mal vielen Dank für die Möglichkeiten die Sie mit dieser Seite eröffnen.
Ich sitze gerade an der Auswertung einer wissenschaftlichen Arbeit und vergleiche 2 nicht parametrisch verteilte Wertepaare < 20 Individuen miteinander. Es geht um die Veränderung festgelegter in einem festgelegten Zeitraum und zur Analyse der Wertepaare habe ich den Wilcoxon Test angewandt. Mein Frage ist jetzt, welcher Wert am repräsentativsten ist um die intraindividuelle Konstanz der Werte (bzw. die nur minimale Veränderung) am besten darzustellen ((großes p/ Spearman Approx. Koeffizient oder der Median der Differenz beider Werte).
Gearbeitet habe ich mit M. EXEL, Graph Pad und BIAS
Vielen Dank im Voraus!
Beste Grüße!
Jonas
Hallo Jonas,
um zu zeigen, dass es nur eine kleine Veränderung gibt, ist der Median der Differenzen, eventuell mit Angabe eine Konfidenzintervalls, gut geeignet.
Schöne Grüße
Daniela
Hallo, Frau Keller,
Ich bin auch neu in der Arbeit mit SPSS und habe einige Fragen,vielleicht können Sie mir helfen.Ich möchte mithilfe von t- test Gruppen von Befragten ohne Abitur und mit Abitur als höchsten Bildungsabschluss in der Intention der Internetnutzung vergleichen.Variable -„Intention der Internetnutzung“ gibt es nicht ,ich habe nur 2 Indizes über Internetnutzung ,die ich gebildet habe. Meine Frage lautet: kann ich diese Indizes nehmen und die in t-test verwenden. Außerdem ist mir nicht klar, zu welcher Skalenniveau Index gehört und was man machen soll, wenn die abhängige Variable nominal oder ordinal oder Index ist ?
Vielen Dank Ihnen im Voraus
Liebe Grüße
Anna
Liebe Anna, danke für deinen Kommentar! Deine Antwort findest du in der Facebook-Gruppe Statistikfragen. 🙂
Hi,
ich habe nur ganz kurz eine Frage und zwar will ich zwei Gruppen, ja und nein vergleichen. Ich will einfach darstellen, dass in der einen Gruppe n=8 ist und in der anderen Gruppe n=40 und dass es sich dabei um einen signifikanten Unterschied handelt. Welchen Test soll ich nehmen?
Gruß Anna
Hallo Anna,
das geht mit dem Chi-Quadrat-Anpassungstest.
LG
Daniela
Hallo Daniela,
ich soll zwei Farbpatronen desselben Herstellers darauf kontrollieren, ob die neuere der zwei eine höhere Lebensdauer hat. Beide enthalten noch die selbe Menge Tinte.
Muss ich hier von verbundenen Stichproben ausgehen?
Danke im Voraus!
Hallo Raphael,
ich tippe auf unverbundene Stichproben. Aber hast du von jeder Art Patrone mehrere? Also mehrere neue und mehrere alte? Oder jeweils nur eine? Dann wäre es gar keine Stichprobe…
Schöne Grüße
Daniela
Hallo Daniela,
ich finde deine Seite total toll :-). Und noch toller, dass man dir hier Fragen stellen kann. Ich möchte vergleichen, ob es einen Unterschied bei Fragebögenantworten bei Versuchspersonen gibt. Ich wollte dazu einen Wilcoxon-Test berechnen. Bei den Absolut-Differenzen, gibt es jedoch viele Rangbindungen, daher müsste ich ja mit der Standardnormalverteilung weiterrechnen. Ich habe jedoch nur 24 Versuchspersonen und wenn ich die Differenzen, die Null sind, abziehe, ist n = 17. SPSS macht daher, glaube ich, keine Normalverteilungs-Approximation (erst ab 25). Gibt es eine Möglichkeit, dass SPSS dies doch macht? Oder was würdest du mir jetzt empfehlen? SPSS gibt mir jedoch ein Ergebnis mit „U = -1.534“ raus. Was ist das hier für eine Prüfgröße? Ich kenne U nur vom Mann-Whitney-U-Test und das ist eigentlich doch immer recht groß…. Oder ist es besser einen anderen Test zu benutzen?
Tausend Dank und viele Grüße,
Katrin
Hallo Katrin,
ich vermute, du vergleichst verbundene Messungen, deshalb der Wilcoxon-Test. Den kannst du auch mit wenigen Fällen und bei Bindungen verwenden. Der passt also. Was ist denn der p-Wert dazu?
Übrigens kannst du Fragen seit kurzem noch besser in meiner geschlossenen Facebook-Gruppe Statistikfragen stellen: https://www.facebook.com/groups/785900308158525/?ref=bookmarks
Schöne Grüße
Daniela
Hallo Frau Keller!
Ich glaube, dass meine Frage recht einfach ist, ich konnte jedoch nirgends eine Antwort darauf finden:
Ich muss für die Diskussion meiner Dissertation Überlebenswahrscheinlichkeiten (selbe Kriterien vorausgesetzt) verschiedener Studien und Durchschnittswerte verschiedener Studien miteinander vergleichen.
Ab welcher Differenz kann ich von „vergleichbaren“ Ergebnissen sprechen? Gibt es da einen festgelegten Bereich? (Z.B. +- 5%)
Kann ich bei Überlebenswahrscheinlichkeiten von 97% und 92% von „vergleichbaren“ Ergebnissen sprechen?
Vielen Dank!
Alex
Hallo Alex,
dafür gibt es keinen festgelegten Bereich, da die Sicherheit, mit der die Werte geschätzt wurden, stark von der Streuung und der Stichprogengröße abhängt. Stattdessen solltest du mit Konfidenzintervallen arbeiten (die hoffentlich in den Studien angegeben wurden).
Schöne Grüße
Daniela
Hallo Frau Keller,
vielen Dank für Ihre Antwort 🙂
Schöne Grüße
Jan
Hallo Frau Keller,
wenn in einer wissenschaftlichen Arbeit mehrere Ergebnisse (sieben Ergebnisse) des t-Tests berichtet werden sollen ist eine Darstellung in Tabellenform angebracht und korrekt nach APA6? Oder müssen die Ergebnisse immer im Text dargestellt werden?
Schöne Grüße und vielen Dank im Voraus!
Jan
Hallo Jan,
eine Darstellung als Tabelle ist genauso in Ordnung wie die Darstellung im Text.
Schöne Grüße
Daniela Keller
Hallo Daniela,
auch von mir nochmals vielen, vielen Dank für deine Hilfe. Das ist wirklich klasse. Ich habe noch eine kleine Frage bzgl. des Wilcoxon Tests. Ich habe ein quasi-experimentelles Design mit einer Experimental-und einer Kontrollgruppe. Ich habe zu zwei verschiedenen Zeitpunkten eine Befragung an diesen beiden Gruppen durchgeführt. Jedoch kann ich die Fragebögen und demnach die einzelnen Daten nicht den einzelnen Personen zuordnen, da ich keine Interpretation auf Individualebene benötige. Es handelt sich doch aber bei dem Vergleich von Experimentalgruppe zu Messzeitpunkt 1 und von Experimentalgruppe zu Messzeitpunkt 2 um eine abhängige Stichprobe, oder? Kann ich trotzdem an dieser Stelle den Wilcoxon Test durchführen? Ich blicke da bei SPSS hinsichtlich der Eingabe gar nicht durch.
Vielen, vielen Dank im Voraus und mit lieben Grüßen,
Petra
Hallo Petra,
es handelt sich bei Ihnen um verbundene Daten. Allerdings ist die Berechnung des Wilcoxon-Tests nicht möglich, wenn die Zuordnung der Messungen zu den Patienten nicht möglich ist. Eigentlich würden die Messungen in zwei Spalten in der Datenmatrix stehen, so dass die Messungen eines Patienten nebeneinander stehen. Ohne eine Zuordnung ist das nicht möglich. Dann ist auch kein Test möglich und es bleibt nur die beschreibende Statistik (Mittelwerte, Standardabweichungen…) und Abbildungen zu verwenden.
Schöne Grüße
Daniela Keller
Hallo Daniela, ich möchte 2 Gruppen von jeweils n=20 vergleichen. Gruppe A wies bezüglich eines Merkmals einen Fehler in 4 Fällen auf (n=4), Gruppe B wies diesen Fehler in 1 Fall (n=1) auf. Ist der Unterschied signifikant?
Über eine Antwort würde ich mich freuen,
mit freundlichem Gruß,
Jonas
Hallo Jonas,
das kann mit Fishers Exaktem Test untersucht werden.
Schöne Grüße
Daniela Keller
Hallo Daniela,
ich habe zwei Messreihen von jedem Patienten, also einmal mittels Sonographie gemessen und einmal mit einer anderen Bildgebung. Das sind doch verbundene Stichproben richtig? wie finde ich nun heraus ob diese Werte normalverteilt sind oder nicht? würde mich über eine Antwort sehr freuen.
Viele Grüße
Anna
Hallo Anna,
ja, das sind verbundene Stichproben. Die Normalverteilung überprüfen Sie am besten mit Quantilplots (auch QQ-Plots oder Normalverteilungsplots genannt).
Schöne Grüße
Daniela Keller
Hallo Daniela,
erstmal muss ich sagen, dass ich es super finde wie Du den Leuten hier weiterhilfst 🙂
Da ich Neueinsteiger bin habe ich nun auch einige Fragen:
Und zwar habe ich eine Studie mit zwei Gruppen (eine stimulierte Gruppe und eine Scheingruppe). Zu vier Messzeitpunkten will ich schauen, ob sich die stimulierte Gruppe signifikant zur Scheingruppe verändert hat.
So wie ich das sehe ist meine Stichprobe unverbunden und normalverteilt (nach Anwendung des Lg10).
Welches Verfahren würdest Du nun zur Ermittlung möglicher Unterschiede verwenden, ich tendiere bis jetzt zu einer ANOVA ?
Ich wäre Dir sehr dankbar wenn Du mir weiterhelfen könntest.
Liebe Grüße,
NIls
zu den vier Messzeitpunkten werden Zeiten verglichen, wie lange eine Person für eine Aufgabe benötigt.
Hallo Nils,
interessiert Sie der Unterschied zu jedem Zeitpunkt? Dann wäre das ein t-Test für jeden Messzeitpunkt extra. Oder interessiert Sie der unterschiedliche Verlauf? Dann wäre das eine ANOVA mit einem Gruppenfaktor und den 4 Messzeitpunkten.
Schöne Grüße
Daniela Keller
Hallo,
ich habe im Rahmen eines quasi-experimentellen Designs nach der ersten Befragung die einzelnen Mediane der Variablen in Abhängigkeit von Experimental- und Kontrollgruppe berechnet. Nun habe ebenso aufgrund des Vorhandenseins von Ordinalskalen einen Mann-Whitney U Test durchgeführt. Nun bekomme ich aber ganz unterschiedliche Ergebnisse im Vergleich zum Mediantest heraus. Beim Mediantest waren alle Hypothesen nicht signifikant (die Mediane der einzelnen Gruppen sind identisch). Beim U Test hingegen wurden einige Hypothesen als signifikant angegeben. Kann so etwas sein?
Vielen vielen Dank!
Liebe Grüße,
Petra
Hallo Petra,
ja, das kann sein. Der Mann-Whitney U Test arbeitet mit den Rängen der Daten, also nicht mit den Originaldaten und damit auch nicht mit dem Median. Deshalb kann das Ergebnis von Mediantest und Mann-Whitney U Test unterschiedlich sein.
Der Mediantest hat eine zu geringe Teststärke (Power). Das heißt, es fällt ihm schwer, Unterschiede als signifikant aufzudecken. Deshalb sollten Sie lieber den Mann-Whitney U Test verwenden, der eine bessere Teststärke hat und deshalb grundsätzlich vorzuziehen ist.
Schöne Grüße
Daniela Keller
Hallo, können nur intervallskalierte Daten normalverteilt sein?
Nein, es erweisen sich auch manchmal ordinale Daten als normalverteilt, zum Beispiel Likert-Skalen.
Hallo Daniela,
ich würde gerne einen Nachweis für eine Neuerung erbringen und bin mir über den Weg noch nicht ganz sicher. Hierfür wird ein Artikel verändert und um ca. 1% verbessert. Er werden dann ganz viele Messungen einer bestimmten Größe vorher und nacher vorgenommen, um den Nachweis zu erbringen.
Kann ich hierbei nun von einer verbundenen Gruppe ausgehen und den Wilcoxon-Test zur Hand nehmen oder muss ich einen anderen Weg einschlagen oder bin ich hier bereits auf dem Holzweg?
Vielen Dank und schöne Grüße,
Tom
Hallo Tom,
ich bin mir noch nicht ganz sicher, tendiere aber eher dazu, das als unabhängige Messungen anzusehen. Können Sie die Angaben etwas präzisieren? Was ist der Artikel, was ist die Verbesserung, was wird gemessen? Alles an einem Objekt vorher und nachher und mehrmals?
Schöne Grüße
Daniela Keller
Vielen Dank für Ihre Antwort.
Es geht darum den Widerstand eines Reifens zu reduzieren. Dieser wird mit Spray eingesprüht. Danach soll sich der Widerstand um 1% reduzieren. Da die Messungen eine gewisse Ungenauigkeit haben, werden sehr viele der benötigten Messgrößen vor und nach der „Behandlung“ durchgeführt. Gemessen und verglichen wird im Grunde der Widerstand, der durch Messung verschiedener Größen errechnet wird. Es wird aber immer der selbe Reifen verwendet.
Ich danke Ihnen für Ihre Antwort.
Gruß,
Tom
Danke für die Erklärungen! Dann sind es unabhängige Messungen. Abhängige Messungen wären es dann, wenn Sie mehrere Reifen hätten, an denen Sie jeweils einmal vor und einmal nach der Behandlung messen. Dann ist jeweils der Vorher-Wert abhängige vom Nachher-Wert, da dieses Wertepaar jeweils am gleichen Reifen gemessen wurde. Wenn Sie insgesamt nur einen Reifen haben, sind es aber unabhängige Messungen.
Schöne Grüße
Daniela Keller
Danke schön!