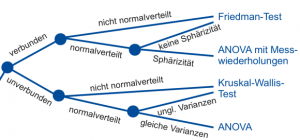
Werden mehr als zwei Gruppen auf Unterschied in der Lage untersucht, so hängt die Wahl der Methode genauso wie beim Vergleich von zwei Gruppen von der Art und der Verteilung der Daten ab. Zunächst sind folgende Fragen zu beantworten:
- Sind die Gruppen verbunden oder unverbunden?
- Sind die Werte für alle Gruppen normalverteilt?
Wenn unverbundene Stichproben vorliegen, die normalverteilt sind, so muss zusätzlich überprüft werden, ob die Stichproben gleiche Varianzen haben. Ist das der Fall, so wird die Varianzanalyse (ANOVA, ANalysis Of VAriance) verwendet.
Wenn die unverbundenen Stichproben nicht normalverteilt sind oder ungleiche Varianzen haben, so wird die nichtparametrische Alternative – der Kruskal-Wallis-Test verwendet.
Hat man verbundene normalverteilte Stichproben, wird überprüft, ob Sphärizität vorliegt. Ist dies der Fall, so verwendet man die ANOVA mit Messwiederholungen.
Gilt keine Sphärizität, so kann man eine Korrektur verwenden (z.B. Greenhouse-Geisser Korrektur), oder man setzt die nichtparametrische Alternative zur ANOVA mit Messwiederholungen ein: den Friedman-Test.
Der Friedman-Test wird grundsätzlich auch verwendet, wenn verbundene nicht normalverteilte Stichproben vorliegen.
All diese Methoden geben die jeweilige Teststatistik und den p-Wert zurück. Ist der p-Wert größer als 0,05, so kann kein signifikanter Unterschied zwischen den Gruppen nachgewiesen werden (was nicht heißt, dass es keinen gibt).
Ist der p-Wert kleiner 0,05, so gibt es einen signifikanten Unterschied (signifikant auf dem Niveau 0,05) zwischen den Gruppen. Die Antwort auf die Frage, wo genau dieser Unterschied liegt, also zwischen welchen Paaren, liefern diese Methode nicht. Das muss anschließend mit so genannten Post-Hoc-Tests (Paarvergleiche) untersucht werden.

Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.


Hallo,
was ich mich immer wieder frage: Ist es nicht problematisch bei Gruppenvergleichen, wenn eine von bspw. drei miteinander zu vergleichenden Gruppen fast vier Mal so groß ist wie die beiden anderen?
Insbesondere bei nicht-parametrischen Verfahren könnte das zu Problemen führen, oder?
Wie verhalte ich mich zudem, wenn die Gruppen nicht nur so unterschiedlich groß sind, sondern auch noch die Variation der Variable in jeder Gruppe ziemlich klein ist (also wenn ich z.B. Noten vergleiche, die aber nur in den Abstufungen von 1 bis 2, 5 vorliegen)? Sind das nicht alles Gegebenheiten, die die Interpretation der Ergebnisse erschweren?
Viele Grüße,
Lisa
Hallo Lisa,
grundsätzlich ist die unterschiedliche Stichprobengröße kein Problem, solange die Voraussetzungen für die Tests erfüllt sind. Bei der ANOVA wäre das zum Beispiel zusätzlich zur Normalverteilung die Varianzhomogenität (Gleichheit der Varianzen). Die wäre in Deinem Beispiel durch die geringe Variation in jeder Gruppe aber nicht verletzt. Die nicht-parametrischen Verfahren haben solche Voraussetzungen nicht, deshalb gibt es hier auch kein Problem.
Ein Problem, das bei ungleichen Stichproben auftauchen kann ist das gleiche, das es auch bei kleinen Stichproben gibt: durch die zu geringe Stichprobengröße (in einer Gruppe) kann ein deutlicher Unterschied eventuell nicht als signifikant nachgewiesen werden.
Deshalb sollte grundsätzlich immer die Größe der Stichproben im Hinterkopf behalten werden, wenn ein statistisches Testergebnis interpretiert wird.
Die geringe Variation ist wie gesagt kein Problem. Was in Deinem Beispiel eher ein Problem sein könnte ist, dass es bei den Noten zwischen 1 und 2,5 nur so wenige Abstufungen gibt. Da müssen die einzelnen Gruppen schon deutlich auseinander liegen (Median) und möglichst wenig innerhalb einer Gruppe streuen (IQR), damit ein Unterschied nachweisbar ist.
Schöne Grüße
Daniela
Guten Morgen Daniela,
noch eine Frage zum Gruppenvergleich:
Wenn ich wissen möchte, ob sich Gruppen hinsichtlich eines kategorialen Merkmals unterscheiden, benutze ich dafür den Chi-Quadrat-Test (Anzahl Gruppen: 3, Anzahl Ausprägungen kategoriale Variable: 4). Wird diese signifikant weiß ich zwar, dass diese beiden Variablen zusammenhängen und mit Blick auf die Zusammenhangsmaße kann ich auch sehen, wie groß dieser Zusammenhang ist. Ich weiß aber nicht, ob sich alle Gruppen von einander unterscheiden oder ob der Unterschied nur zwischen zwei Gruppen liegt. Was kann ich also machen, um das herauszufinden? Die jeweiligen Gruppen noch einmal in einem Chi-Test jeweils gegeneinander testen und das Signifikanzniveau anpassen (Korrektur wegen Mehrfachvergleichen)? Ach ja: Und natürlich sind die Gruppen unterschiedlich groß, die eine ist fast drei Mal so groß wie die beiden anderen…
Danke und Gruß,
Lisa
Hallo,
ja, wenn der Unterschied zwischen genau zwei Gruppen interessiert, dann müssen genau diese beiden nochmal gemeinsam mit einem Chi-Quadrat Test unersucht werden. Und dann wäre auch eine Anpassung des Signifikanzniveaus notwendig. Die unterschiedliche Größe ist wieder kein Problem.
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für die sehr hilfreichen Ausführungen auf Deiner Homepage. Leider ist ein Punkt der mich besonders interessiert nicht beantwortet, nämlich die Frage von Lisa vom 19. September 2014 betreffend Chi-Quadrat-Test bei einem Vergleich von mehr als zwei Gruppen. Wäre es möglich, darauf eine Antwort zu erhalten?
Besten Dank und Gruss,
Thomas
Hallo Thomas,
danke für Deinen Kommentar. Mir ist bisher nicht aufgefallen, dass da noch eine Antwort aussteht. Ich habe sie eben nachgeliefert.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe 9 Gruppen, die ich miteinander vergleichen will. Sie weisen alle eine Normalverteilung auf, jedoch keine Varianzhomogenität (Levene Test). Mir wurde darauf hin empfohlen den Games-Howell-Test durchzuführen, um herauszufinden, welche Gruppen sich signifikant voneinander unterscheiden. Ich arbeite mit SAS 9.2 und bin leider aus den Ausführungen aud der SAS-support Seite nicht wirklich schlau geworden, wie man einen solchen Test jetzt durchführt. Gibt es im Internet oder Büchern Beispiele/Erklärungen wie man einen solchen Test in SAS durchführt?
vielen Dank
Grüße Claudia
Liebe Claudia,
ich arbeite selbst nicht mehr mit SAS und kann deshalb zur Lösung des Problems keine richtige Hilfestellung geben. Was ich auf die Schnelle gefunden habe ist folgendes:
LSMEANS Statement verwenden, dort ADJUST=TUKEY und ADJDFE=ROW als Options angeben.
Als sehr gute Hilfestellung kann ich Ihnen das Buch von Andy Field empfehlen (nicht günstig, aber das beste Statistikbuch das ich kenne): Discovering Statistics Using SAS http://www.amazon.com/Discovering-Statistics-Using-Andy-Field/dp/1849200920
Ich verwende die Bücher von Andy Field (gleicher Aufbau, fast gleicher Inhalt) für SPSS und für R und kann sie WÄRMSTENS empfehlen. Sie enthalten sehr sehr viele Methoden und die Umsetzung, Interpretation und Verwendung ist didaktisch sehr gut aufgearbeitet (und dazu noch unterhaltsam 🙂 ). Ich denke, bei der Version für SAS wird das genauso sein.
Schöne Grüße
Daniela Keller
Hallo,
ich will die Hypothese untersuchen, dass die von uns durchgeführten Interventionen bei Männern und Frauen den gleichen Effekt ihre Planungskompetenz haben. Die Daten sind nicht normalverteilt und leider besteht keine Varianzhomogenität zwischen den Geschlechtergruppen zu beiden Messzeitpunkten (die Gruppen sind unterschiedlich groß). Dabei wollte ich eigentlich eine mehrfaktorielle Varianzanalyse mit Messswiederholung rechnen. Oben in der Grafik steht, dass man den Kruskal-Wallis Test machen kann, der gibt mir ja aber bei 2 Gruppen das gleiche Ergebnis wie der Mann-Whitney U Test und keine Interaktion. Weißt du, wie ich die Hypothese berechnen kann?
Vielen lieben Dank im Voraus für die Hilfe!=)
Hallo Alina,
es gibt keine nichtparametrische Methode für mehrfaktorielle Modelle. Aber du kannst dir eventuell behelfen, indem du statt der beiden Messzeitpunkte dir nur die Differenz „Nachher minus Vorher“ anschaust. Dann kannst du diese Differenzwerte zwischen Männern und Frauen vergleichen und siehst, ob sie sich unterscheiden (unterschiedliche Änderung der Planungskompetenz). Das geht dann wieder mit dem nichtparamterischen Mann-Whitney U Test.
Alternativ gibt es in SPSS auch die Varianzanalyse mit Bootstrap, die auch verwendet werden kann, wenn die Voraussetzungen nicht gegeben sind.
Du kannst gern unserer neu gegründeten Facebook-Gruppe Statistikfragen beitreten: https://www.facebook.com/groups/785900308158525/
Dort kannst du weitere Fragen stellen und mit mir und den anderen Teilnehmern darüber diskutieren.
Schöne Grüße
Daniela
Hallo!
Welche Möglichkeiten bestehen normalverteilte Daten zu erzeugen? Ich habe zum Beispiel gezählte Werte als orginal Daten. (Oozysten)
Hier sind auch viele Werte =0. Das Transformieren (log) führt leider nicht zu einer Normalverteilung…
Hallo, wenn Nuller enthalten sind, muss bei der Logtransformation eine Konstante dazu gezählt werden, z.B. 1: y=log(x+1) mit y = transformierte Variable, x= Originalvariable. Denn der Logarithmus von 0 ist nicht definiert. Würde man log(x) verwenden, würden alle Beobachtungen, die vorher 0 waren, aus der Analyse heraus fallen. Eine andere Möglichkeit der Transformation ist die Wurzel. Vielleicht klappt die bei dir besser. Auch hier kannst du eventuell eine Konstante dazu zählen, um das Ergebnis zu verbessern (zwingend notwendig ist es hier nicht).
Hallo Frau Keller,
ich habe eine Frage bezüglich dem Vergleich von mehr als zwei Gruppen:
Ich möchte metrisch verteilte Daten in verschiedenen Altersgruppen (3) vergleichen. Die Daten sind nicht normal verteilt. Nun habe ich zuerst den Kruskal-Wallis-Test angewendet. Die Gruppen unterscheiden sich signifikant. Doch welcher Test ist nun der richtige um alle 3 Gruppen untereinander zu vergleichen, z.B. ob sich Altersgruppe 1 von 2 und 3 unterscheidet?
Vielen Dank für die Hilfe auf diese wahrscheinliche banale Frage.
Hallo, meinst du Paarvergleiche, also 1 mit 2, 1 mit 3 und 2 mit 3? Dann ist es Mann-Whitney U.
Weiterführende Fragen könnt ihr gern mit mir und den anderen Teilnehmern in der Facebook-Gruppe Statistikfragen diskutieren. Hier der Link: https://www.facebook.com/groups/785900308158525/
Liebe Frau Keller,
mir liegen Daten der Ergebnisse von 5 Tests vor. Gerne möchte ich den Zusammenhang zwischen dem Testergebnis von Test 1 und den anderen Testergebnissen sowie von Test 1 und dem Gesamtwert der 4 anderen Testergebnisse überprüfen. Bei Testergebnis 1 handelt es sich um eine Variable mit 3 Abstufungen, bei den 4 anderen Tests um eine kontinuierliche Variable. Jede Person hat beide Tests durchgeführt. Meine erste Frage ist die Folgende: Ist es möglich, in diesem Fall eine ANOVA zu rechnen, oder was wäre das geeignetste Testverfahren für diesen Fall? Die zweite Frage lautet: Wie behandele ich den Gesamtscore aus den 4 Testverfahren, wie eine zusätzliche Variable?
Viele Grüße
Lisa
Hallo Lisa,
ja, in dem Fall passt die ANOVA. Und ja, den Gesamtscore behandelst du wie eine zusätzliche Variable.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe eine Varianzanalyse durchgeführt zum Vergleich verschiedener religiöser Gruppen. Du sagtest weiter oben, dass die Gruppengrößen nicht so wichtig sind, wenn die Voraussetzungen erfüllt sind. Meine Gruppengrößen sind allerdings: 130, 75, 3, 3, 2, 3, 79. Ist da eine Untersuchung überhaupt sinnvoll oder sollten die Gruppen mit nur 2-3 Teilnehmern aus der Analyse ausgeschlossen werden? Und falls nicht: Würde das dann mein Gesamtergebnis beeinflussen (also Gruppen unterscheiden sich signfikant/nicht signifikant voneinander)?
Noch eine kleine Frage: Wie kann man bei SPSS die Normalverteilung der Residualvariablen überprüfen? Das ist doch eine zentrale Voraussetzung der VA, oder?
Liebe Grüße, Katrin
Hallo Katrin,
die kleinen Gruppengrößen mit 3 und 2 sind nicht so gut. Kannst du die vielleicht alle zusammen packen unter „andere Religionen“? Du kannst sie aber auch drin lassen. Es wird aber schwierig, einen Unterschied zwischen diesen und von diesen zu den anderen Gruppen nachzuweisen, da die Gruppen zu klein sind. Ganz weglassen ist aber auch möglich. Wie es für deine Fragestellung besser passt.
Die Voraussetzung der ANOVA ist, dass die abhängige Variable in den einzelnen Gruppen normalverteilt ist.
Schöne Grüße
Daniela
PS: also ist die folgende Syntax zur Überprüfung der Normalverteilung der Residuen richtig?
EXAMINE VARIABLES=ZFIS_Gesamt BY SD28
/PLOT BOXPLOT STEMLEAF NPPLOT
/COMPARE GROUPS
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
Ich habe mir dadie Kolmogorov-Smirnov-Ergebnisse ansehen. Die sind leider bei einer Gruppe nicht normalverteilt und bei den Gruppen mit nur 2-3 Leuten ist ein Punkt. Heißt wohl, dass das nicht berechnet werden konnte, oder?
LG und vielen Dank vorab!!
Ja, die kleinen Gruppen sind zu klein für diese Überprüfung. Ansonsten passt das. Ich sehe mir statt der Tests hier immer lieber die Q-Q-Diagramme an. Die Tests sind manchmal zu streng.
Liebe Daniela,
wie ist das weitere Vorgehen, wenn ich keine Varianzhomogenität gegeben habe (2-Faktorielle ANOVA)? Gibt es eine Alternative?
Oder ist es unwichtig, da ich sowieso keinen Interaktionseffekt herausbekommen habe? (Oder hätte ich einen finden können, wenn die Varianzhomogenität gegeben wäre?)
Liebste Grüße
Lotta
Hallo Lotta,
für die mehrfaktorielle ANOVA gibt es robuste Versionen z.B. in der Software R. SPSS liefert hier keine (im Gegensatz zur einfaktoriellen ANOVA, wo es z.B. die Welch-Anpassung gibt). Wenn die Varianzhomogenität nicht gegeben ist, ist das Ergebnis der ANOVA nicht zuverlässig. Du kannst also nicht vom Ergebnis der ANOVA darauf schließen, ob die Verletzung der Varianzhomogenität ein Problem ist oder nicht…
Wie sieht es mit der Normalverteilung aus? Könnte eine Transformation etwas nützen?
Schöne Grüße
Daniela
Liebe Daniela,
ich würde gerne eine 2×2 Varianzanalyse mit SPSS durchführen. Auch in meinem Fall sind die Gruppen sehr ungleich (n=8, n=80, n= 150, n = 155). Der Größenunterschied in den Gruppen spiegelt tatsächliche Verhältnisse wieder.
Gibt es eine Richtlinie bzgl. einer Mindestzellenbesetzung? Könnte der Vergleich dieser Gruppen ein Problem darstellen? – Oder ist auch hier, wie Du bereits mehrmals geschrieben hast, nur wichtig, dass die Voraussetzungen (Homogenität und NV) gegeben sind?
Wäre dir für eine Antwort überaus dankbar.
Viele Grüße
Jenny
Hallo Jenny, ja genau, solange die Voraussetzungen erfüllt sind, ist alles in Ordnung.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe ein Kollektiv von 50 Patienten, bei dem die Schwere der Erkrankung vier Ausprägungen annehmen kann. Nun möchte ich herausfinden, ob in den einzelnen Schweregraden Unteschiede bezüglich Alter, Erkrankungsdauer und verschiedenen anderern Parametern vorliegen.
Liege ich da mit dem Kruskal-Wallis-Test richtig?
Vielen Dank im Voraus,
Lisa
Hallo Lisa,
ja, wenn der Parameter nicht normalverteilt ist, dann Kruskal Wallis. Wenn Normalverteilung vorliegt geht auch die ANOVA.
Gruß
Daniela
Liebe Daniela,
ich habe eine generelle Frage zu einem Diskussionspunkt. In meiner Untersuchung haben die Teilnehmerinnen meinen Fragebogen zum Affekt nur sehr selten (in 4 Tagen durchschnittlich 10x) ausgefüllt. Was für statistische Einschränkungen gilt es aufgrund dessen zu diskutieren?
Vielen Dank und liebe Grüße,
Hanni
Hallo Hanni, geht es dir um die große Anzahl fehlender Werte bei der Analyse? Wieviele fehlen denn in den einzelnen Analysen tatsächlich?
Schöne Grüße
Daniela
Hallo Daniela,
prinzipiell ja, die Personen hätten den Fragebogen 25x am Tag ausfüllen müssen. Dabei ist er mindestens 1x und maximal 18x ausgefüllt worden. Durchschnittlich nur 9x bei n=12. Ich habe die Werte dann einfach über den jeweiligen Tag gemittelt. Jetzt stellt sich mir die Frage wie ich das in der Diskussion am besten…naja diskutieren kann. Da das Ergebnis so ja sicherlich nur eingeschränkt interpretierbar ist. Abgesehen von der kleinen Stichprobe 😉
Vielen Dank!
Naja, ich würde es auf jeden Fall so beschreiben, wie du es hier genannt hast: Wie oft minimal, maximal, im Schnitt. Da dich aber ja scheinbar der Tag insgesamt und nicht der Verlauf interessiert hat, macht das nichts für die Analyse. Damit aber der Leser richtig die Datenqualität einschätzen kann, solltest du die Entstehung der Daten einfach so nennen.
Vielen Dank!
Hallo Daniela,
ich will meine Stichprobengröße a-priori mit G*Power berechnen. Mein Versuchsdesign ist eine 3×3 ANOVA mit Messwiederholung (within-subject Design)
Was trage ich genau bei „Number of groups“ und bei „Number of measurements“ ein?
Vielen Dank für deine Hilfe
Beste Grüße
Lena
Hallo Lena,
Number of Groups ist die Anzahl der Gruppen des Gruppenfaktors, Number of Measurements ist die Anzahl der Messwiederholungen des Messwiederholungsfaktors. Ob G*Power auch bei komplexeren Designs geht, kann ich grade nicht sagen. Wenn du da was heraus findest, poste es doch bitte hier!
Schöne Grüße
Daniela
Hallo Daniela,
ich habe folgendes Problem: Ich möchte gerne vier verschiedene Gruppen miteinander vergleichen. Eine der Gruppen ist nicht normalverteilt, daher habe ich mich bei der globalen Varianzanalyse für den Kruskal-Wallis-Test entschieden. Wenn ich diesen in SPSS mit anschließendem Paarvergleich durchführe, gibt es einen signifikanten Unterschied zwischen den Gruppen 1 zu 3, 2 zu 3 und 1 zu 4.
Wenn ich die Post-Hoc-Tests aber manuell durchführe, also mittels Mann-Whitney-U-Test dann finde ich auch einen signifikanten Unterschied zwischen den Gruppen 1 und 2 (und das auf einem angepassten Signifikanzniveau nach Bonferroni). Wie kann das sein?
Bin ich überhaupt richtig vorgegangen oder hätte ich in diesem Fall, obwohl bei einer Gruppe keine Normalverteilung gegeben ist, auch mit ANOVA testen können?
P.S. Gruppe 2 ist genau die Gruppe, bei der keine Normalverteilung vorliegt.
Viele Grüße,
Anna
Hallo Anna,
wie genau sind die p-Werte beim Vergleich von 1 und 2 bei den beiden unterschiedlichen Methoden?
Gruß
Daniela
Hallo,
ich habe folgende Ausgangslage:
keine Normalverteilung, verbundene Stichproben (da Messwiederholung) – ergibt also den Friedman-Test
Mir ist jedoch noch nicht ganz klar, wie ich den Test ausführen soll bei unterschiedlichen Stichprobengrößen bzw. fehlenden Werten.
Habe ich beispielsweise eine Variable, die ich zu 5 Zeitpunkten untersuche, konnte aber aus verschiedenen Gründen nicht in jedem Fall alle 5 Zeitpunkte erheben (weil beispielsweise der Proband nicht aufgetaucht ist), wie kann ich den Test dann durchführen?
Hallo Lena,
du kannst hier immer nur die kompletten Fälle betrachten. Die, bei denen ein oder mehrere Messwerte fehlen, können bei einer Analyse über alle 5 Messzeitpunkte nicht mit verwendet werden.
Schöne Grüße
Daniela
Hallo Daniela,
ich bin bin am überlegen ob ich parametrische Verfahren verwenden kann oder nicht. Ich möchte untersuchen ob sich vier Gruppen hinsichtlich ihrem Wohlbefinden unterscheiden. Ich habe eine Stichprobe von 820 Probanden.
Die Skala Wohlbefinden ist nicht normalverteilt und deutlich linksschief. Ich habe aber jetzt schon so oft gelesen, dass das bei so einer großen Stichprobe kein Problem ist. Deswegen bin ich mir jetzt nicht sicher, ab wann die Normalverteilungsvoraussetzung zu stark verletzt ist.
Die Varianzen sind auch nicht homogen. Aber da habe ich auch wieder gelesen, dass das bei größeren Stichproben nicht so schlimm ist.
Und die Probandenzahl in den vier Gruppen unterscheidet sich auch. (70,350,200,200)
…Eigentlich würde ich gerne einfach nicht-parametrische Verfahren nehmen, da kann man irgendwie nicht so viel falsch machen. Aber da ich das alles begründen muss, warum ich das „schlechtere“ Verfahren verwende, bin ich mir da jetzt nicht so sicher.
Liebe Grüße,
Rebekka
Hallo Rebekka,
es gibt Untersuchungen, dass die ANOVA ab 10 (manche sagen auch ab 30) pro Gruppe robust auf die Abweichung der Normalverteilung reagiert. Allerdings sollten dann die Gruppengrößen ungefähr gleich groß sein, was bei dir nicht der Fall ist. Auch auf Abweichungen von der Varianzhomogenität gilt sie bei gleich großen und genügend großen Gruppen als robust. Schau mal in den Bortz, da steht dazu was zitiert.
Und: Warum ist das nicht-parametrische Verfahren „schlechter“? 🙂
Schöne Grüße
Daniela
Danke für die schnelle Antwort! Voll nett 🙂
Bei den nicht parametrischen Verfahren habe ich immer den Eindruck, dass sie in der Literatur eher als unumgänglichen Ausweg gesehen werden, wenn die Voraussetzungen für parametrische Verfahren überhaupt nicht erfüllt sind.
Zu den unterschiedlich großen Gruppen (70,200,200,350) hätte ich noch eine Nachfrage. Wäre es insgesamt eleganter aus den großen Gruppen jeweils zufällig 70 auszuwählen? Oder könnte ich das auch irgendwie begründen, dass ich die Gruppen so lasse? (weil ich es irgendwie schade fände so viele Probanden verschütt gehen zu lassen). Man soll ja auch die Stichprobe möglichst rational planen.
Liebe Grüße 🙂
Hallo Rebekka,
die nichtparametrischen Verfahren haben eine etwas geringere Teststärke, das heißt, sie brauchen ein wenig mehr Beobachtungen, um den gleichen Unterschied als signifikant nachzuweisen. Das ist aus statistischer Sicht ein Grund, warum sie als „schlechter“ angesehen werden könnten. Dieser Unterschied ist aber nicht groß.
Die Gruppen würde ich so lassen und nicht per Zufallsauswahl reduzieren. Dann wirklich lieber den nichtparametrischen Test nehmen, wenn die Voraussetzungen nicht passen.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe mich für meine Analyse (Scores von drei verschiedenen Gruppen) an Deinem Entscheidugsbaum orientiert und lande beim Friedman-Test. Das Ergebnis ist signifikant.
Wie kriege ich raus, welche Gruppen sich sig. voneinander unterscheiden? Ich arbeite mit SAS.
Vielen Dank und viele liebe Grüße
Fabian
Hallo Fabian,
dazu kannst du Post-Hoc Tests verwenden. Ich weiß nicht, welche da in SAS implementiert sind. Falls es keine implementierten gibt, kannst du selbst mehrere Wilcoxon-Tests rechnen und das Fehlerniveau dann selbst anpassen (wegen multiplem Testen ist das dann notwendig), z.B. mit Bonferroni-Holm.
Schöne Grüße
Daniela
Liebe Frau Keller,
ich habe wieder eine wichtige Frage an Sie, bei der ich gerade nicht recht weiter komme. Ich führe eine ANOVA mit Messwiederholung in einem 4x3x2-Design mit 7 AV´s durch, meine Daten können jedoch bei zwei abhängigen Variablen fehlende Werte (Missings) enthalten. Nun schließt SPSS die kompletten Datensätze der Versuchspersonen bei fehlenden Werte aus, was ca ein Drittel meiner Datensätze betrifft – nicht wirklich praktisch.
Nun ist es so, dass fehlende Werte entstehen, wenn eine Versuchsperson nicht innerhalb einer maximalen Entscheidungszeit eine Wahl trifft (Time Out), wodurch dann die Entscheidungszeit selbst (AV1) und die Entscheidungsqualität (AV6) als fehlend bezeichnet wird. Zugleich wird noch erfasst, ob es bei der Person einen Time Out (AV2) gab.
Meine Überlegung war nun, zwei getrennte ANOVAS mit Messwiederholung durchzuführen und dabei die AV1 und AV6 separat von den anderen abhängigen Variablen zu analysieren (deren N aufgrund der Missing kleiner ist). Die Variable Time Out (AV2) wird dann separat mit den übrigen Variablen anhand der Gesamtstichprobe untersucht und bietet eine inhaltliche Verbindung zur anderen ANOVA mit den fehlenden Werten.
Das erscheint mir zwar ein praktisches Vorgehen zu sein, leider kann ich nicht einschätzen ob es legitim ist so vorzugehen oder ob ich grundsätzlich eine andere Auswertungsmethode nutzen sollte (was in Anbetracht des Abgabezeitpunktes meiner Arbeit nicht so praktisch wäre).
Wie schätzen Sie das ein?
Liebe Grüße
Stephan
Hallo Stephan,
so kannst du natürlich vorgehen. Wenn du mit den Ergebnissen dann etwas anfangen kannst, wenn du also diese beiden Ergebnisse dann sinnvoll für deine Fragestellung interpretieren kannst, ist das völlig in Ordnung. Zwei andere Ideen, die mir spontan gekommen sind:
1. Ist es möglich, für diese fehlenden Werte feste Werte einzusetzen, z.B. bei der Entscheidungszeit die maximale Zeit plus eine Konstante? Bei der Entscheidungsqualität den schlechtesten Wert? Dann wären die Daten vollständig. Vermutlich sind sie dann aber nicht mehr normalverteilt, wenn es sich um ein Drittel der Daten handelt…
2. Grundsätzlich kann man bei fehlenden Werten mit Multlevel-Linearen-Modellen rechnen. Allerdings ist das recht komplex und wohl kurzfristig nicht umsetzbar.
Das sind nur zwei spontane Ideen. Wie gesagt ist dein Vorschlag auch in Ordnung, wenn das Ergebnis vor dem Hintergrund deiner Forschungsfrage interpretierbar ist.
Schöne Grüße
Daniela
Hi Daniela,
vielen Dank für deine Einschätzung – das hilft mir ungemein weiter!
Ja, das mit dem Vervollständigen der Daten hatte ich auch schon überlegt und mich in das Verfahren der multiplen Imputation gefuchst. Dabei ist mir jedoch aufgefallen, dass ich diese Werte aus inhaltlicher Perspektive ja gar nicht ersetzen will, weil, wer keine Entscheidung in der maximal möglichen Zeit treffen konnte, konnte es einfach nicht und dieser Umstand ist für meine Forschungsfrage und dazugehörige Interpretation zentral. Mein Gedanke dazu ist, dass ein Vervollständigen der Daten über diesen Umstand hinwegtäuschen würde und mögliche künstliche Verzerrungen in den Daten der Personen verursachen könnten, die eine Entscheidung treffen konnte. Anyway…
Ganz glücklich bin ich mit der „2-ANOVA-Lösung“ jedoch auch nicht, da ja auch bei der separaten ANOVA mit den fehlenden Werten (Entscheidungszeit und Qualität) nur die Fälle aufgenommen werden, bei denen zu keinem der drei Messzeitpunkte ein fehlender Wert vorliegt. Damit habe ich das Grundproblem wohl in die zweite ANOVA weitergetragen aber die Auswirkungen reduziert, da nun nur die abhängigen Variablen betroffen sind die, die auch fehlende Werte verursachen.
Vielen Dank nochmals Daniela und eine gute Zeit
Stephan
Hallo Stephan,
eine Imputation der fehlenden Werte würde ich nicht machen, denn die setzt voraus, dass die fehlenden Werte zufällig sind und man sie aus der Struktur der restlichen Daten schätzen kann. Das ist hier aber ganz klar nicht der Fall. Es sind ja gerade spezielle Fälle (zu lange Reaktionszeit), die fehlen. Deshalb war mein Vorschlag, das mit einem extremen Wert zu ersetzen. Aber wie gesagt, wird da wohl dann keine Normalverteilung mehr raus kommen.
Schöne Grüße
Daniela
Hallo Daniela,
ein kurze Frage: Ich möchte drei unterschiedliche (aber kleine) Gruppen miteinander vergleichen in Bezug auf mehrere Variablen kodiert als ja/nein (0 und 1). Würde dies‘ aber gerne nicht von Gruppe zu Gruppe (A vs. B, B vs. C, A vs. C) machen, sondern mit einem einzigen p-Wert zeigen, daß grundsätzlich ein Unterschied zwischen den Gruppen besteht. Geht das ebenfalls mit dem Fisher’s exact test (in SPSS)?
Hallo Sven,
da es drei Gruppen sind, wäre das der Chi-Quadrat-Test. Die kleine Gruppengröße könnte aber hier problematisch werden. Dann kannst du (zumindest in SPSS) die Fisher-Anpassung verwenden, findest du über die Schaltfläche „Exakt“.
Schöne Grüße
Daniela
Hallo Frau Keller,
ich habe in meinem Experiment drei Gruppen (2 Experimentalgruppen + 1 Kontrollgruppe). Alle drei Gruppen sind nahezu gleichgroß (EG1=25 / EG2=25 / KG=26) Zudem sind sie unverbunden und normalverteilt, was somit auf eine Varianzanalyse schließen lässt.
Ich erhalte nun ein NICHT signifikantes Ergebnis zwischen den Gruppen. Dies bedeutet ja dann, dass es keinen Unterschied zwischen den gruppen gibt.
Wie finde ich nun heraus, ob es überhaupt einen Effekt der UV auf die AV gibt?
Wie gehe ich nun mit weiteren metrischen Einflussvariablen vor? Kann ich dazu trotzdem die Kovarianzanalyse verwenden, in dem ich in mehreren Modellen überprüfe, ob eine Mediation oder Moderation vorliegen könnte?
Vielen Dank und mit freundlichen Grüßen
Marlene
Hallo Marlene,
wenn du mit UV die Gruppen meinst, dann hast du schon herausgefunden, dass sie keinen Effekt hat.
Für weitere metrische Einflussvariablen nimmst du sie als Kovariaten mit auf. Oder du rechnest gleich eine mehrfaktorielle lineare Regression. In beiden Fällen musst du jeweils die besonderen Voraussetzungen beachten!
Schöne Grüße
Daniela
Hallo Daniela,
ich habe 3 gleich starke, aber kleine Gruppen (unverbunden). In 2 der 3 Gruppen sind nicht alle Werte normalverteilt. Ich habe dann geschaut, wie das Ganze aussieht, wenn ich die Daten umwandel, aber da zeigt sich keine Veränderung. Soweit ich richtig gerechnet habe, besteht Varianzhomogenität, wobei das hier keine Rolle mehr spielen dürfte.
Die Auswertung würde ich mit Kruskal-Wallis machen, aber ich bin mir nicht sicher, ob ich das auf alle meine Daten anwenden kann.
Ich habe 4 AVs von denen es Zeitdaten gibt und 3 AVs deren Daten als relative Häufigkeiten angegeben sind. Brauche ich da ein anderes Analyseverfahren?
Die deskriptive Statistik kann ich in einem machen und in einer Tabelle abarbeiten, egal ob Zeiten oder Häufigkeiten?
Freue mich auf Antwort, danke!
Hallo Mare,
die deskriptive ist für alle gleich. Ansonsten entscheidest du nach Normalverteilung ja/nein, ob du Kruskal-Wallis oder die ANOVA verwendest.
Schöne Grüße
Daniela
Hallo Daniela,
in meiner Untersuchung habe ich ein 2×4 Versuchsdesign gewählt, da ich eine av,eine uv mit zwei Abstufungen und 4 Messwiederholungen habe.Es werden 2 Gruppen betrachtet je n=15.
Daraufhin habe ich beschlossen eine Zweifaktorielle Varianzanalyse zu berechnen,da ich aber noch zwei Kovariate habe,habe ich eine Kovarianzanalyse mit 4 Messwiederholungen durchgeführt mit der SPSS Software.Wäre das bis zu diesem Punkt richtig?
Das Problem hat sich dann ergeben als ich mittels eines Q-Q Diagrammes die Daten der abhängigen Variable geprüft habe und auf das Ergebnis gestoßen bin,dass sie nicht normalverteilt sind.
Ist das erstmal richtig um die Normalverteilung zu überprüfen?
Eigentlich müsste ich jetzt doch den U Test durchführen oder?Aber was mache ich mit den Kovariaten?
Nun wurde mir von einem Statistik Dozent folgende Anmerkung zugetragen:
– Die ANOVA sei robust gegenüber Verletzungen der Normalverteilungsannahme
– Eine verletzte Normalverteilungsannahme allein sei kein Grund die ANOVA nicht durchzuführen
– Die Residuen sind es, die normalverteilt sein sollen
Jetzt bin ich völlig durcheinander,es wäre toll,wenn du mir helfen könntest!
Schöne Grüße
Josepha
Hallo Josepha,
deine Methodenwahl war richtig. Es stimmt, dass die ANOVA robust auf Verletzugnen der Normalverteilungsannahme reagiert, wenn die Fallzahl genügend groß ist und es stimmt auch, dass eigentlich die Residuen normalverteilt sein müssen. Zudem ist auch immer die Frage, wie du die Verteilung untersucht hast, es gibt dafür strenge und weniger strenge Methoden…
Eine nichtparametrische Alternative zu deinem Studiendesign gibt es nicht.
Schöne Grüße
Daniela
Hallo Daniela,
ich schlage mich gerade mit folgendem Problem herum:
Es wurde die Wirkung eines Präparates gegenüber eines Placebos getestet. Die Wirkung wurde über 3 Zeitpunkte geprüft (Baseline, 6 Wochen, 12 Wochen).
Sowohl das Präparat als auch das Placebo zeigte im Vergleich zur Baseline eine signifikante Veränderung (Friedman-Test).
Aus der Differenz der Messzeitpunkte zur Baseline (d.h. 6Wochen-Baseline und 12Wochen-Baseline) zeigte jeweils einen signifikanten Unterschied zwischen der Gruppe, die das Präparat bekamen zu der Gruppe, die das Placebo erhielten (Mann-Whitney-U-Test).
Nun wurde eine Varianzanalyse mit Messwiederholungen (repeated measurement) verlangt. WIe muss ich so etwas berechnen bei nicht-parametrischen Daten? Und stimmt es, dass ich bei parametrischen Daten einfach eine univariate Analyse mache mit der Zeit als Co-variate?
Danke für Deine HIlfe
Michael
Hallo Michael,
du bräuchtest wohl eine ANOVA mit Messwiederholung und Gruppenfaktor. Die gibt es im nichtparametrischen Fall nicht. Wie groß ist deine Stichprobe und wie hast du die Verteilung geprüft?
Schöne Grüße
Daniela
Hallo!
Ich habe eine abhängige Stichprobe mit einer AV in 3 Abstufungen und einer UV in 2 Abstufungen (=Gruppe) ich möchte eine Varianzanalyse mit Messwertwiederholungen machen mit der AV in den 3 Abstufungen als Innersubjektfaktor und der UV al zwischensubjektfaktor. Die UV setzt sich zusammen aus der Punkteanzahl bei einem Test und die Vp habe ich in 3 Gruppen (Extremwerte) unterteilt ich möchte die Extremwert-Gruppe 1 vs. Gruppe 3 im Hinblick auf die AV untersuchen.
Doch leider liegt keine Normalverteilung in der UV vor.
Dann müsste ich also einen Friedmantest rechnen, aber wie kann ich beim Friedmantest 2 Gruppen vergleichen? Bei SPSS kann ich nur die 3 AV eingeben. Muss ich die Daten vorher in 2 Gruppen teilen? Darf man das?
Bin durch das viele Rechnen für meine Masterarbeit schon total verwirrt und hoffe hier auf Hilfe und Aufklärung.
Danke
Hallo Mary,
für eine mehrfaktorielle ANOVA passt der Friedman nicht. Eventuell kannst du deine Daten transformieren und Normalverteiung erreichen? Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Vielen Dank für die Antwort! Warum passt eigentlich der Friedman Test nicht?
Mit Transformieren meinst du Logarithmieren oder? Muss ich dann alle Werte logarithmieren oder falls von den 2 Gruppen nur eine Gruppe nicht normalverteilt ist, nur die Werte dieser Gruppe?
Hallo Mary,
den Friedman gibt es nicht als mehrfaktorielles Modell. Zum Transformieren wäre der Logarithmus möglich, ja, das muss man aber ausprobieren. Wenn eine Transformation passt, dann passt sie normalerweise in allen Gruppen.
Schöne Grüße
Daniela
Hallo Daniela,
das ist wirklich eine tolle Seite. Das E-Book hab ich auch schon. Allerdings stellen sich mir einige Fragen, auf die ich noch keine Antwort gefunden habe.
Ich habe 4 verschiedene (unverbundene) Gruppen. Nun möchte ich alle Gruppen hinsichtlich 4 Variablen (Alter, pH, Laktat, Konzentration eines Medikamentes) vergleichen. Leider sind die Variablen in einer Gruppe nicht normalverteilt. Der Test der Homogenität der Varianzen ergibt auch für 2 der Variablen keine Homogenität. Daher habe ich geschlussfolgert, dass ich einen nicht-parametrischen Test brauche. Also Kursaal-Wallis…allerdings wurde mir dann gesagt, dass das vielleicht nicht geht, da ich ja nicht nur eine Variable, sondern 4 untersuche. Dementsprechend bräuchte ich einen nicht-parametrischen Test der einer MANOVA entspricht oder nicht??? Oder kann ich einfach trotzdem einen Kursaal-Wallis-Test machen und anschließend einen Mann-Whitney-U als post-hoc-Test? Bin inzwischen total durcheinander und für jede Hilfe dankbar!
Viele Grüße,
Katharina
Hallo Katharina,
eine nichtparametrische Alternative zur MANOVA gibt es nicht. Brauchst du wirklich eine MANOVA oder kannst du auch jede abhängige Variable für sich betrachten? Dann könntest du nämlich wie du schon erkannt hast für jede Variable den Kruskal-Wallis-Test rechnen (eventuell dann mit Post-Hoc Tests für die Paarvergleiche danach).
Schöne Grüße
Daniela
Hallo Daniela!
DANKE für die schnelle Rückmeldung. Ok, ich denke, dass ich das dann mit dem Kursakal-Wallis mache. Als Post-Hoc-Test müsste ich ja dann den Mann-Whiteny-U machen und dann irgendwie die Mehrfachtestung berücksichtigen oder nicht?
Viele Grüße,
Katharina
Genau.
Hallo Daniela,
vielen Dank für diese tolle Seite und das kostenlose E-Book, das hat mir schon sehr viel weitergeholfen!
Ich sitze gerade an der Auswertung meiner Abschlussarbeit und bin mir unsicher, welches Berechnungsverfahren ich anwenden soll.
Ich habe zu zwei Messzeitpunkten die Konzentrationsfähigkeit (likertskalierte Skala) von Lernenden abgefragt, sowie u.a. die besuchte Schulform (HS, RS, GY). Meine Hypothesen lauten sinngemäß und verkürzt:
1. die Lernkonzentration verändert sich von MZP1 auf MZP2
2. das Ausmaß der zeitlichen Veränderung unterscheidet sich je nach vorheriger Durchschnittsnote (3-stufig) bzw. besuchter Schulform.
Ich möchte damit auf between-subject-Ebene überprüfen, ob sich die Mittelwertdifferenz von MZP1 zu MZP2 zwischen den Schulformtypen unterscheidet und falls ja zwischen welchen genau (dabei möchte ich aber alle 3 Schulformen jeweils paarweise untereinander vergleichen).
Auf within-subject Ebene interessiert mich besonders, ob sich innerhalb der Schulformzugehörigkeit (also z.B. für HauptschülerInnen) eine signifikante Veränderung in der Lernkonzentration über die Zeit feststellen lässt (und das separat für jede Schulform).
Ich habe nun vor aufgrund der Gefahr einer Alpha-Fehler-Kumulation nicht vor, eine Vielzahl an t-Tests für abhängige Stichproben zu berechnen, sondern halte es für sinnvoller, eine zweifaktorielle Varianzanalyse mit Messwiederholung (gemischtes Design) zu berechnen, wobei die AV dann der Messzeitpunkt (MZP1, MZP2) und meine UV eine 3-stufige Gruppenvariable wäre ( Schulformzugehörigkeit „Hauptschule“, „Realschule“, „Gymnasium“). Sollten die Interaktionseffekte signifikant werden, habe ich vor, mir von SPSS zusätzlich post-hoc-Tests mit Bonferroni-Korrektur ausgeben zu lassen.
Reicht das beschriebene Vorgehen so aus bzw. ist es sinnvoll, oder muss ich noch zusätzliche oder ganz andere Berechnungen durchführen (vorausgesetzt die Annahmen für eine ANOVA mit Messwiederholung sind gegeben)? Ich habe z.B. von der Möglichkeit, zusätzliche Kontraste in SPSS berechnen zu können, gelesen.
Ich bin mir sehr unsicher, ob das so passt und würde mich über ein kurzes Feedback von dir sehr freuen!
Vielen Dank schon mal und beste Grüße,
Jasmin
Hallo Jasmin,
bei deiner Fragestellung ist dieses Vorgehen genau richtig. Kontraste wären dann passend, wenn du nicht alle Schulformen paarweise vergleichen willst, sondern hier nur ausgewählte Vergleiche rechnest. Passt also alles so!
Weitere Fragen können gern in meiner Facebookgruppe Statistikfragen diskutiert werden: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Liebe Daniela,
super, vielen Dank für die schnelle Rückmeldung!
Beste Grüße und einen guten Start ins neue Jahr,
Jasmin
Liebe Daniela,
für meine Studie berechne ich mixed design ANOVAs mit Messwiederholung. Ich habe verschiedene Faktoren, die ich berücksichtigen möchte. Sollte ich alle Faktoren in eine Analyse aufnehmen oder sollte ich mehrere Analysen rechnen? Wovon hängt das ab und was ist eigentlich genau der Unterschied?
Herzliche Grüße
Hallo Lisa,
wie komplex das Modell sein kann, hängt davon ab, wie groß die Stichprobe ist. Es ist aber immer sinnvoll, mehrere Modelle zu rechnen und zu vergleichen.
Schöne Grüße
Daniela
Ich habe eine Frage bezüglich der Wahl des Testverfahrens.
Ich untersuche den Unterschied zwischen drei Technologien, die für die gleiche Aufgabe eingesetzt werden.
Jeder Proband führt mit jeder Technologie die Aufgabe aus und nach jeder Ausführung bewertet er den entstanden Workload mittels des NASA Task Load Index aus diesem lässt sie ein Wert für den Workload bestimmen.
Nun möchte ich Vergleichen, ob ein signifikanter Unterschied zwischen den drei Technologien vorliegt.
Ich werde den Versuch mit zwei kleinen Probandengruppen (ca. 10 Probanden) durchführen, d.h. es werden sich wahrscheinlich keine normalverteilten Ergebnisse ergeben.
In erster Linier möchte ich erstmal den Vergleich der 3 Technologien innerhalb einer Gruppe durchführen, um festzustellen ob sich eine Technologie besser eignet. Welcher Test eignet sich hierfür?
Im Anschluss oder falls es ein Verfahren gibt was alles Abdeckt möchte ich den Vergleich zwischen den Gruppen herstellen, d.h. bspw ob es einen Unterschied in der Bewertung der Technologie A gab.
Bei nichtnormalverteilten Daten und 3 Gruppen nimmst Du den Kruskal-Wallis Test.
Schöne Grüße
Daniela
Liebe Daniela,
ich habe 3 verschiedene Gruppen mit jeweils unterschiedlicher Teilnehmeranzahl, weil ich manche Daten nicht verwenden kann. Wäre es sinnvoll, die Gruppengrößen anzupassen, d.h. nachzuerheben oder andere Datensätze rauszustreichen?
LG
Anne
Hallo Anne,
das hängt von vielen anderen praktischen Kriterien ab und lässt sich so pauschal nicht beantworten. Besprich das doch ausführlicher in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela