Wenn ich einen statistischen Test durchführen will, muss ich vorher wissen, ob meine Daten normalverteilt sind oder nicht. Sind sie normalverteilt, so kann ich einen parametrischen Test verwenden. Sind sie es nicht, so muss ein nichtparametrischer her. Für den Vergleich zweier Gruppen wäre das bei Normalverteilung der berühmte t-Test. Wenn keine Normalverteilung vorliegt, der Mann-Whitney-U Test.
| Parametrisch | Nichtparametrisch | |
| Daten | normalverteilt | nicht normalverteilt |
| Vergleich von 2 unabhängigen Stichproben | t-Test | Mann-Whitney-U Test |
| Vergleich von 2 abhängigen Stichproben | gepaarter t-Test | Wilcoxon Paarvergleichstest |
| Vergleich von mehr als 2 unabhängigen Stichproben | einfaktorielle Varianzanalyse | Kruskal-Wallis-Test |
| Vergleich von mehr als 2 abhängigen Stichproben | Varianzanalyse mit Messwiederholungen | Friedman-Test |
| Korrelation zwischen 2 Stichproben | Pearson-Korrelation | Spearman-Korrelation |
Du willst mehr Durchblick im Statistik-Dschungel?
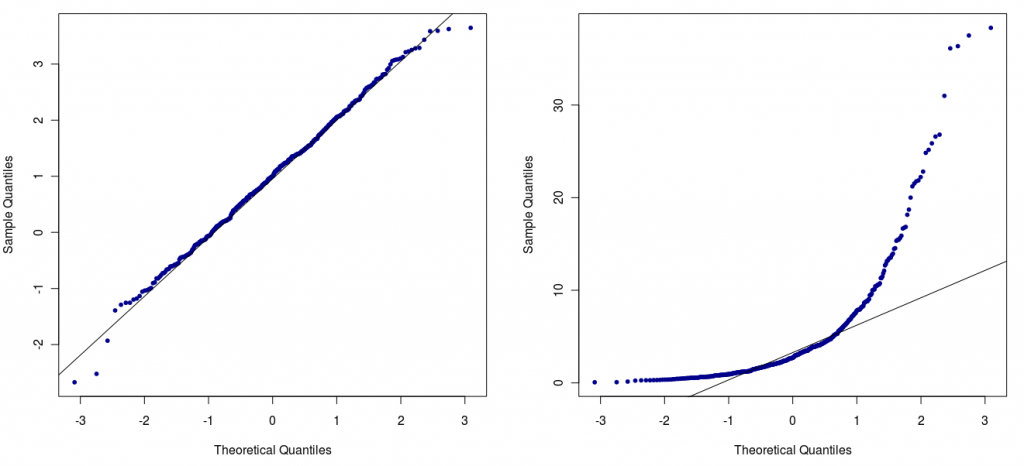
Wie erkenne ich, ob meine Daten normalverteilt sind? Am besten, man sieht sich einen Normalverteilungsplot an, und zwar für jede Gruppe einzeln. Dort werden die Daten gegen die erwarteten Werte einer Normalverteilung geplottet. Liegen die Punkte schön auf einer Geraden, so sind die Daten normalverteilt. Es gibt auch Tests, die auf Normalverteilung untersuchen, z.B. Shapiro-Wilk, aber die sind oft zu streng. Meiner Meinung nach ist der optische „Test“ hier das Mittel der Wahl. 
Wenn die Punkte nicht schön auf einer Geraden liegen, können sie vielleicht durch eine Transformation normalverteilt „gemacht“ werden. Insbesondere dann, wenn die Punkte in einem Bogen um die Geraden liegen, ist das möglich. Die häufigste Transformation ist der Logarithmus: einfach die Daten logarithmieren und damit noch einmal einen Plot machen. Ist das Ergebnis nun gut? Dann waren die Originaldaten lognormalverteilt. Die transformierten Daten sind nun normalverteilt und können zur Analyse mit parametrischen Verfahren verwendet werden. Kann auch durch eine Transformation keine Normalverteilung erreicht werden, ist das auch kein Beinbruch. Für viele Verfahren gibt es nichtparametrische Alternativen. Diese dürfen übrigens auch auf normalverteilten Daten angewandt werden. Mit ihnen kann man also (fast) nichts falsch machen.
Wenn die Punkte nicht schön auf einer Geraden liegen, können sie vielleicht durch eine Transformation normalverteilt „gemacht“ werden. Insbesondere dann, wenn die Punkte in einem Bogen um die Geraden liegen, ist das möglich. Die häufigste Transformation ist der Logarithmus: einfach die Daten logarithmieren und damit noch einmal einen Plot machen. Ist das Ergebnis nun gut? Dann waren die Originaldaten lognormalverteilt. Die transformierten Daten sind nun normalverteilt und können zur Analyse mit parametrischen Verfahren verwendet werden. Kann auch durch eine Transformation keine Normalverteilung erreicht werden, ist das auch kein Beinbruch. Für viele Verfahren gibt es nichtparametrische Alternativen. Diese dürfen übrigens auch auf normalverteilten Daten angewandt werden. Mit ihnen kann man also (fast) nichts falsch machen.
Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.
Hallo, ich habe den klassischen Fall einer Therapie-Wirksamkeitsstudie: Vorher-Nachher-Vergleich mit Follow-Up. Das sind somit verbundene/abhängige Stichproben.
Ich habe zu den verschiedenen Messzeitpunkten T-Werte und Prozentränge von Entwicklungstests erhoben. Bisher habe ich angenommen, dass ich den T-Test machen kann. Jetzt wurde mir gesagt, dass ich wegen der PR und T-Werte aber ein nonparametrisches Verfahren nutzen muss. Der Entwicklungstest würde ja eigentlich Scores nutzen und die Daten erst nachträglich normalverteilt aussehen lassen. Stimmt es, dass ich nicht parametrisch testen darf?
Ich habe noch eine zweite Schwierigkeit:
Mein Problem ist, dass die Leistung der Patienten in Prozenträngen bzw. T-Werten gemessen werden, diese aber manchmal auch als Spanne angegeben werden. Zum Beispiel: Patient X erreicht einen Rohwert von 46 und daraus ergibt sich in dem Leistungstest ein T-Wert zwischen 9,45 und 13,54.
Mit welchen Werten rechne ich denn dann? Nehme ich den Durchschnitt von 9,45 und 13,54? Ist inhaltlich so ja nicht korrekt.
Vielen Dank schon einmal im Voraus
Hallo Phia,
wenn Spannen statt Messwerte verwendet werden, handelt es sich um ordinale Daten, dann darfst Du tatsächlich nur nichtparametrische Verfahren einsetzen. Ansonsten, bei Messwerten, T-Werten, Prozenträngen, kannst Du die Verteilung prüfen und wenn Normalverteilung gegeben ist parametrisch testen.
Schöne Grüße
Daniela
Hallo Daniela,
ich hätte da auch mal eine Frage. Wir führen gerade eine Evaluation durch und haben zuerst durch den Kolmogorov- Smirnov- Test getestet, ob eine Normalverteilung vorliegt. Unsere Stichprobe besteht aus zwei Gruppen, die wir allerdings wie eine Grupp ansehen. Zwei unserer 15 Skalen sind leider nicht normalverteilt, allerdings müssen wir nun einen T-Test mit einer nicht-normalverteilten Skala und einer normalverteilten Skala machen. Unsere Frage ist daher, ob wir einen normalen T- Test hierfür machen können und dadurch davon ausgehen, dass unsere Stichprobe normalverteilt ist, oder ob wir den Mann- Whitney- U- Test machen sollen?
Vielen lieben Dank für die Hilfe schon im Voraus,
Julia
Hallo Julia,
wenn der untersuchte Parameter in einer oder beiden Gruppen nicht normalverteilt ist, solltest Ihr den Mann-Whitney U Test verwenden.
Schöne Grüße
Daniela
Hallo,
Ich habe ordinalskalierte Werte. Da ja die Voraussetzung für ein parametrisches Verfahren (z.B.t-Test) die Normalverteilung sowie eine Intervallskalierung ist, ist es wohl nicht mehr notwendig die Werte auf Normalverteilung zu überprüfen oder? Weil dann kann ich gleich mit einem nicht-parametrischen Verfahren (z.B: Mann-Whitney-U-Test) beginnen. Bzw. falls die Überprüfung auf Normalverteilung notwendig wäre, macht man das bei ordinalskalierten Skalen anhand des Medians? oder nimmt man da auch den Mittelwert?
Grüße
Katy
Hallo Katy,
richtig, bei ordinal-skalierten Werten greifst Du gleich auf die nichtparametrischen Verfahren zurück.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Ich hätte auch eine Frage…. Und zwar gibt es in unserer Klausur folgende Aufgabe: Man hat eine neue Therapieform und will diese gegen zwei andere Therapieform testen hinsichtlich ihrer Effektivität. Wie macht man das?
Ich hatte daran gedacht eine Dreifaktorielle ANOVA mit Messwiederholung zu rechnen und dann einen Post-Hoc Test durchzuführen, um zu sehen, ob sich die drei Gruppen voneinander unterscheiden. Habe ich damit die Fragestellung erfüllt oder fehlt jetzt z.B. noch etwas konkretes zur Effektivität?
Hallo,
das kommt darauf an, mit welchem Parameter die Effektivität gemessen wird, wie der verteilt ist usw. Eine dreifaktorielle ANOVA mit Messwiederholung sehe ich hier aber nicht…
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela,
ich vergleiche zwei Gruppen (Patienten/Kontrollen) und werde mehrere T-Tests machen müssen, da ich sehr viele Variablen habe. Dann muss ich jede Variable einzeln und für beiden Gruppen getrennt auf Normalverteilung überprüfen, oder? Und dann bei den Variablen, die normalverteilt sind den T-Test und bei nicht-normalverteilten den U-Test? Oder ist der T-Test unzulässig sobald nur eine Variable in der Stichprobe nicht normalverteilt ist.
Würde mich so sehr auf eine Antwort freuen.
Alina
Hallo Alina,
ja, Du entscheidest für jede Variable einzeln, ob Du t-Test oder U-Test verwendest. Wenn Du es Dir einfacher machen willst, kannst Du auch immer U-Test nehmen, denn der ist auch erlaubt, wenn Normalverteilung vorliegt.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Liebe Daniela,
ich schreibe zur Zeit meine Masterarbeit und habe eine Frage zum Test auf Normalverteilung.
Die Gesamtpopulation beträgt n=28 und diese werden in Verum und Placebo unterteilt. Schaue ich mir nun jeweils Placebo und Verumgruppe separat an, um zu schauen, ob die Werte in den einzelnen Gruppen normalverteilt sind, oder schaue ich mir die Gesamtpopulation an?
Lieben Dank im Voraus für deine Antwort.
Liebe Grüße, Riki
Hallo Riki,
das kommt darauf an, wie Du die Daten später im Test verwendest. Wenn Du sie da in Gruppen (Verum und Placebo) unterteiltst, dann musst Du sie auch so gruppiert auf Normalverteilung prüfen.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe eine kurze Frage meine Werte sind nicht normalverteilt und ich habe kleine Stichprobengrößen. Kann ich trotzdem 95% Konfidenzintervalle angeben, obwohl diese eigentlich nur auf normalverteilte Werte anwendbar sind? Oder ist es besser sich auf die Angabe von Median und evtl. Mittelwert +/- Standardabweichung zu beschränken. Ich danke dir vielmals für deine Hilfe!
Schöne Grüße
Juliane
Halo Juliane,
Mittelwert, Standardabweichung und Konfidenzintervall passen dann nicht perfekt, deshalb würde ich (zumindest zusätzlich) auf jeden Fall noch Median angeben und Min/Max und eventuell 25% und 75%-Quantil.
Schöne Grüße
Daniela
Liebe Daniela,
danke für diese übersichtlichen und klaren Erklärungen, die sind wirklich äußerst hilfreich.
Ich hätte eine Frage bzgl. des Projekts meiner Masterarbeit.
Ich habe in einer Grundschulklasse eine Methode im Vokabellernen im Experimental- Kontrollgruppendesign in Form von Vokabeltests getestet. Dafür habe ich den gleichen Test in beiden Gruppen drei Mal innerhalb von 2 Monaten wiederholt.
Leider hat sich heraus gestellt, dass nicht alle Testergebnisse normal verteilt sind, somit kann ja wahrscheinlich keine T-Tests machen.
Ich möchte untersuchen, ob sich die Behaltensleistung zwischen den beiden Gruppen unterscheidet und das Experiment einen Effekt hatte, also die Experimentalgruppe in den Tests besser abschneidet. Ist es dann richtig, in dem Falle den Mann Whitney U Test anzuwenden?
Ich möchte auch die Entwicklung der Testergebnisse innerhalb der jeweiligen Gruppen vergleichen (also z.B. MZP1 und MZP 3 innerhalb der Experimentalgruppe), um zu sehen, ob sich die Testergebnisse über die Zeit hinweg verbessern. Ist es richtig, dass ich das dann mit dem Wilcoxon Test mache?
Könnte ich dann trotzdem zusätzlich in meiner Beschreibung der Ergebnisse die Mittelwerte der Testergebnisse nennen, oder dürfte ich das nur, wenn ich auch T-Test berechnet hätte?
Über ein Feedback würde ich mich sehr freuen, da ich nicht einschätzen kann, ob mein Vorgehen so korrekt ist, da ich bisher nur Erfahrungen mit T-Tests gemacht habe und hoffte, das würde auch diesmal wieder passen.
Vielen Dank im Voraus,
Vera
Hallo Vera,
die Auswahl der Tests so ist richtig, und Du kannst natürlich auch die Mittelwerte dazu nennen. Wenn die Daten aber extrem schief sind, passt der Median besser. Wenn Du Dir beide ansiehst (Median und Mittelwert), wird Dir das auffallen.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela,
erstmal danke für die tolle Zusammenfassung. Mein statistisches Problem ist aber glaube ich simpler.
Ich habe derselben Gruppe vor und nach einem bestimmten Zeitraum drei Fragen auf einer fünfstufigen Skala gestellt und daraus gewichtet einen Indikatorwert (0,4*Antwort(1)+0,4*Antwort(2)+0,2*Antwort(3)) ermittelt. Nun würde ich gerne eine Aussage über den Unterschied der beiden Indikatorwerte (vor und nach dem Zeitraum) machen. Gibt es da eine praktische Methode, diesen Unterschied mithilfe eines Tests oder ähnlichem mathematisch zu untermauern?
Die Indikatorwerte sind dabei jeweils die Mittelwerte über die gesamte Gruppe. Es geht also um den Vergleich von zwei Werten.
Hallo Lennart,
Du hast zwei verbundene Stichproben (Messwiederholung vor/nach) und eine abhängige Variable (Indikator). Wenn der Indikator normalverteilt ist, nimmst Du den t-Test für verbundene Stichproben, um den Unterschied auf Signifikanz zu prüfen. Liegt keine Normalverteilung vor, nimmst Du den Wilcoxon-Test. Das und weitere Infos, was noch möglich ist, finste Du in meinem kostenlosen E-Book: https://statistik-und-beratung.de/gratis-e-book-statistische-datenanalyse-die-grundlagen/
Schöne Grüße
Daniela
Hallo Daniela.
Super gut erklärt und eine tolle Übersicht! Vielen Dank!
Muss ich, wenn ich eine Abschlussarbeit nach APA schreibe erklären, warum ich Q.-Q.-plots für die Feststellung von Normalverteilung verwende und nicht Kolmogorov-Smirnov und/oder Shapiro-Wilk?
Falls ja, gibt es dafür gängige Literatur, die erklärt, dass KS-test und SW-test (zu) streng sind?
Oder ist es auch generell anerkannt die Normalverteilung mittels Q.-Q.-plots zu testen und bedarf keiner weiteren Erklärung?
Würde mich sehr über eine kurze Antwort freuen.
Lieben Dank,
Conny
Hallo Conny,
die Bewertung per Q-Q-Plots ist ein gängiges Verfahren. Wenn Du es genauer begründen willst, dann z.B. über Andy Field (Discovering Statistics using SPSS). Er sagt explizit, dass die Tests zu streng sind.
Schöne Grüße
Daniela
Guten Abend,
ich bin gerade etwas erschrocken, habe aber die Stelle in meinem Buch wiedergefunden, in der es heißt: „Eine Annahme des t-Tests ist, dass die AV i.d. Population normalverteilt ist. Unter bestimmten Umständen darf diese Voraussetzung jedoch verletzt sein, ohne dass das Ergebnis des t-Tests dadurch verzerrt ist. Wenn beide Stichproben jeweils mindestens 30 Personen umfassen, gilt der zentrale Grenzwertsatz: […]“
Genau das ist bei mir der Fall: Ich habe eine große Stichprobe (N > 500) und meine AV ist nicht normalverteilt (deutliche Abweichungen von der Referenzgeraden im Q-Q-Plot). Ich darf doch trotzdem den t-Test für unabhängige Stichproben rechnen, oder? Varianzenhomogenität ist geprüft worden.
Tolle Seite! Viele Grüße
Hallo Lis,
ja, bei einer so großen Fallzahl ist der t-Test robust.
Weitere Fragen gern in der Facebookgruppe Statistikfragen posten: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Frau Keller,
Gibt es ein nichtparametrisches Pendant zur einfachen linearen und zur multiplen Regression in SPSS?
Danke im Voraus 🙂
Hallo,
nein, eine nichtparametrische Version gibt es nicht. Aber es gibt die Möglichkeit, z.B. Bootstrapping zu verwenden.
Weitere Fragen können gern in meiner Facebookgruppe Statistikfragen diskutiert werden: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Sehr geehrte Frau Keller
Ich hoffe Sie können mir helfen.
Ich habe 6 Personen die 100 Würfe machen müssen. Ich möchte den Wurf der einzelnen Personen über die 100 Schüsse analysieren. Ich weiss dass bei allen Personen keine Normalverteilung vorhanden ist. Habe deshalb die 100 Schüsse in 4 Gruppen geteilt und anschliessend den Friedman test durchgeführt.
Meine Frage betrifft nun aber die deskriptive Statistik bei einer nicht Normalverteilung. Welche Daten sind geeignet anzugeben? Ich dachte an Min, Max, Mean, Median,Q1, Q2 (um Outlier zu beschreiben)?
Stimmt es das ein Konfidenzintervall und SD nicht sehr sinnvoll ist?
Vielen Dank für Ihre Hilfe und herzliche Grüsse
Manuela
Hallo Manuela,
bei schiefen Daten und/oder Ausreißern passt die Angabe des Medians, Q1, Q2 und Min und Max gut. Mittelwert, SD und Konfidenzintervall können der Schiefe nicht gerecht werden und werden extrem von Ausreißern beeinflusst.
Schöne Grüße
Daniela
Hallo Frau Keller,
im Zuge meiner Abschlussarbeit möchte ich gerne ein theoretisches Modell mit insgesamt 12 Variablen betrachten, deren Werte ich jeweils anhand mehrerer Items pro Variable erfragt habe. Ich habe jedoch das Problem, dass ich ein Unternehmen bzw. einen Bereich untersuche, in der die Stichprobe nur n=14 beträgt und mehr auch nicht möglich ist.
Ziel ist es eigentlich, signifkante Korrelationen zwischen den Variablen aufzudecken (z.B. auch vier unabhängige auf eine abhängige Variable). Da parametrische Tests m.M.n. aufgrund der zu geringen Stichprobe nicht genutzt werden können (?), ist mein Geganke, die Korrelaion auf Basis nicht-parametrischer Tests zu berechnen. Da es hierbei jedoch nur um bivariate Beziehungen geht und nicht multivariate, kann ich mein Modell so wohl kaum analysieren oder?
Ich hoffe ich habe mein Problem einigermaßen verständlich schildern können. Über Anregungen würde ich mich sehr freuen. Danke!
Hallo Daniel,
wie schon in der Facebook-Gruppe geantwortet würde ich hier rein auf bivariate Zusammenhänge gehen und alles schön ausführlich deskriptiv darstellen und diskutieren.
Schöne Grüße
Daniela
Sehr geehrte Frau Keller,
ich hoffe Sie können mir weiterhelfen.
Meine AV ist metrisch, nicht normalverteilt.
Durch bivariate nichtparametrische Tests habe ich den Zusammenhang zu anderen Variablen getestet. Dabei gab es einen signifikanten Zusammenhang zwischen einer nominal dichotomen Variablen, was meine Hauptthese unterstützt.
Außerdem gab es einen signifikanten Zusammenhang mit weiteren metrischen, nicht normalverteilten Variablen. Im nächsten Schritt möchte ich diese weiteren Variablen als Kovariate betrachten. Jedoch wird die Voraussetzung für eine Kovarianzanalyse nicht erfüllt, da die AV nicht normalverteilt ist. Welchen anderen Test könnte ich hier anwenden?
Vielen Dank im Voraus!
Hallo Rufina,
eine nichtparametrische Alternative zur Kovarianzanalyse gibt es nicht. Eventuell lässt sich die abhängige Variable durch Transformation in eine NOrmalverteilung überführen? Für weitere spezielle Fragen – nicht direkt zum Blogbeitrag hier – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela
Zuerst ein grosses Lob für all die guten Erklärungen! Ich habe 3 Gruppen mit jeweils 4 Proben und möchte wissen ob es signifikante Unterschiede gibt. Die Daten sind nicht normal verteilt (in einer Gruppe z.B. 0,0,0,14 Larven pro 100 Früchte), also habe ich den Kruskal-Wallis Test verwendet der mir auch signifikante Unterschiede bestätigte. Wenn ich allerdings die einzelnen Gruppen mit dem Mann-Whitney-U Test vergleiche gibt es mit der Bonferroni Korrektur (0.05 / 3 = 0.017) keinen signifikanten Unterschiede. Wie kann das sein und sind die Unterschiede signifikant oder nicht?
Vielen Dank und herzliche Grüsse
Hallo Laura,
die Bonferroni-Korrektur ist sehr konservativ, deshalb kann das durchaus vorkommen, dass nach der Korrektur kein signifikantes Ergebnis mehr vorliegt. Für weitere spezielle Fragen – nicht direkt zum Blogbeitrag hier – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Dort tummeln sich viele mit ähnlichen Problemen und auch Antworten dazu und ich schaue auch regelmäßig vorbei.
Schöne Grüße
Daniela
Liebe Daniela,
ich habe diese Seite gefunden und finde sie sehr hilfreich – das E-Book habe ich mir schon durchgelesen und es war einiges klarer. Ich wollte in SPSS einen Kruskal-Wallis Test machen – der leider nicht funktioniert.
Zu den Daten (n=110):
Ich habe per Zufallsauswahl 4 Artikel ausgeben lassen (dies ist also meine UV, mit. je min. n=20) und zu diesen die immer gleichen Fragen gestellt. Eine der wichtigsten Zusammenhänge ist die Beurteilung des Artikels mit 5-stufiger Likert Skala (also AV). Ich möchte nun also die Unterschiede der Beurteilung ermitteln, die sich in Abhängigkeit der unterschiedlichen Artikel ergeben haben.
Der Artikel ist als ordinale Variable, numerisch mit den Werten 1-4, in SPSS angelegt. Verteilung ist laut S-W/K-S Test nicht Normalverteilt. Diese Variable habe ich als Gruppe behandelt. Scheinbar habe ich ein falsches Verständnis von „Gruppe“.
Frage 1: Ist meine Gruppe zu groß für die oben genannten Tests auf Normalverteilung, sollte ich also von NV ausgehen? Das QQ-Diagramm zeigt schon eine annähernde Verteilung, aber eben auch ein leichtes S. Daher hate ich die Signifikanz ketestet, die .000 ergeben hat.
Frage 2: Ist der Umgang mit den Daten aus der Zufallsauswahl korrekt?
Über einen Rat würde ich mich sehr freuen!
Hallo Greta,
deine Vorgehensweise klingt richtig. Ich weiß nicht, warum der Kruskal-Wallis Test nicht funktioniert hat. Für weitere spezielle Fragen – nicht den Blogbeitrag betreffend – kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Liebe Daniela,
erstmal ein dickes Dankeschön für deinen Blog, er hat mein Forschungsprojekt gerettet! 🙂
Du lieferst umfangreiche, sehr gut verständliche Erklärungen, die auch Nicht-Statistiker verstehen. Danke dafür!
Ich forsche im Rahmen meines Masterstudiums. Es gibt zwei unabh. Stichprobengruppen. Habe zunächst jede Gruppe mit Q-Q-Plot auf Normalverteilung geprüft. Sahen ziemlich normal verteilt aus. Der Anderson-Darling-Test meint jedoch, dass keine Normalverteilung für die Gesamtwerte der Gruppe 1+2 vorliegt. Muss ich denn den Test für beide Gruppen einzeln rechnen?
Muss ich Boxplot etc. auch beide Gruppen separat machen oder jeweils einen für die Gesamtversuchspersonen?
Vielen Dank für deine Antwort im Voraus und ein schönes Wochenende,
Carolin
Hallo Carolin,
wenn du später einen Test als Gruppenvergleich rechnest, musst du die Normalverteilung in jeder Gruppe einzeln prüfen. Die Tests auf Normalverteilung sind zu streng. Deshalb empfehle ich, sich immer auch ein Q-Q-Diagramm anzusehen. Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
ich wollte einen gepaarten T-Test rechnen, genau genommen muss ich zwei rechnen, allerdings musste ich jetzt feststellen, dass meine Stichproben nach Fallausschlüssen winzig wurden (2 Personen bzw. 5 Personen). Kann ich den dann überhaupt anwenden? Oder muss ich was anderes machen?
Hallo Ilona,
n=2 ist sehr gering. Damit wird man nur sehr schwierig Unterschiede als signifikant nachweisen. Für spezielle Fragen, nicht direkt zum Blogbeitrag hier, kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
ich hoffe ich komme nicht zu spät mit meiner Frage, da lange nichts mehr gepostet wurde.
Ich bin gerade bei der Auswertung der Daten meiner Masterarbeit. Ich möchte in einem Laborexperiment herausfinden ob die Individuendichte einer Garnelenart auf deren Nahrungsaufnahme einen Einfluss hat. Dazu habe ich die Tiere in 3 Behandlungsgruppen eingeteilt (niedrige, hohe, mittlere Dichte). Für das Experiment standen 60 Aquarienbecken zur Verfügung: 20 Aquarien für jede Gruppe. Innerhalb von 24 h habe ich 5 mal ein Tier aus jedem Becken entnommen und deren Darminhalt überprüft (incl. 4 Replikate, d.h. für jede Behandlung und Probenahmezeitpunkt habe ich 4 Tiere entnommen). Dabei ich nie ein Becken oder ein Tier zweimal beprobt. Ich hoffe das Design habe ich gut erklärt, ansonsten fragen sie mich einfach 🙂
Die Fragen dazu sind nun:
1) Sind die Werte aufgrund des Designs unabhängig voneinander? Ich habe ja kein Tier zweimal beprobt und immer aus einem neuen Becken beprobt.
2) Ich dachte für den Vergleich des Tagesverlaufs des Darminhalts der Tiere zwischen den Behandlungen natürlich gleich an eine ANOVA. Da nicht nur die Behandlung, sondern auch die Zeit ein Faktor ist, habe ich es mit einer zweifaktoriellen ANOVA versucht. Die Residuen waren natürlich nicht normalverteilt.. Meine Frage ist nun.. Gibt es eine nichtparametrische Alternative zur zweifaktoriellen ANOVA? Im Internet steht immer etwas anderes und das verwirrt mich, da ich nicht erfahren in der Statistik bin.
3) Im Freiland wurde ein äquivalentes Experiment auf einem Fluss durchgeführt. Dort geht es aber nicht um den Tagesverlauf der Konsumtion, sondern nur um den Vergleich der mittleren täglichen Konsumtionsrate. D.h. ich habe je Behandlungsgruppe 1 Wert. Da die Raten aber mit einer Berechnungsformel innerhalb einer Bootstrap-Simulation (n=1000) berechnet wurden, habe ich gehört, dass ich keinen „klassischen“ Test verwendet kann. Haben sie da eine Idee, wie ich die Werte vergleichen kann?
Ich bedanke mich schon mal im Voraus für eine Antwort! Ich hoffe ich komme nicht zu spät.
Liebe Grüße,
Anne
Hallo Anne,
die Stichproben müssten meiner Ansicht nach unabhängig sein. Eine nichtparametrische Alternative zur zweifaktoriellen ANOVA gibt es nicht (zumindest nicht in den Standard-Statistik-Programmen). Eventuell lassen sich deine Daten durch Transformation in eine Normalvertielung überführen? Für spezielle Fragen, nicht direkt zum Blogbeitrag hier, kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Liebe Frau Keller,
zunächst vielen Dank für die schnelle Antwort!
Ist es auch möglich bzw. gültig alle Akteure in einer Mehrfachantwort zusammenzufassen und somit in einer Kreuztabelle zu prüfen, ob ein Zusammenhang zwischen Akteursinteresse und Outcome als Ganzes oder in verschiedenen Gruppen ( Interesse von Staat, Wirtschaft, NGO oä. beeinflusst Ergebnis) besteht ?
Bei normalverteilten Daten habe ich das über benutzerdefinierte Tabellen realisieren können, aber nichtparametrische Tests finde ich dort nicht.
Beste Grüße,
Jens
Hallo Jens,
ich weiß nicht, was genau du hier meinst. Normalverteilte Daten und benutzerdefinierte Tabelle/Mehrfachantwort?? Für spezielle Fragen, nicht direkt zum Blogbeitrag hier, kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
in meinem Experiment (1 AV – 3 stufig, mehrere AV, N=30) hat sich herausgestellt, dass meine Messungen abhängig sind. Ich habe 3 Gruppen, die während einer Testung alle Faktorstufen durchlaufen.
Folgendes dazu noch als Info:
1. Die zu messenden Variablen sind in der Bevölkerung eher nicht normalverteilt, bzw. sind individuell sehr verschieden.
2. Die gerechneten Daten (Residuen/AV) sind zum großen Teil auch nicht normalverteilt, was wegen Punkt 1 kein Wunder ist.
In der Praxis scheint es normal, dass trotzdem parametrisch gerechnet wird?!? Ich habe mehrere Arbeiten durchgesehen, die meinem Experiment ähnlich sind und nie war ein nichtparametrisches Verfahren zu sehen.
Nach dem Grenzwerttheorem wäre auch bei den nicht normalverteilten Daten ein parametrisches Verfahren anwendbar?
Die Stichprobe hat das Minimum von 30 und die Gruppengrößen sind gleichstark besetzt.
Wäre dieses Anwendung völlig Humbug, weil davon auszugehen ist, dass in der Bevölkerung eher keine Normalverteilung gegeben ist?
Außerdem noch folgende Fragen:
Für die ANOVA mit Messw. habe ich die Datenmatrix umstrukturiert. Falls parametrisch als Analyseweg besser ist, macht man dann für jede AV eine einzelne Auswertung? Das wäre umständlich, aber ich würde die Analyse und Ergenisse gut verstehen.
Könnte ich alternativ eine MANOVA rechnen?
Eine MANOVA geht auch ohne Umstrukturierung?
Muss ich umstrukturieren, wenn ich Friedman rechnen würde?
Gibt es nach Friedman einen „Post Hoc“ oder sowas wie
t-test für abhängige Variablen?
Vielen Dank für deine Einschätzung und Hilfe
im Voraus.
Hallo Mare,
ja, die ANOVA gilt als robust auf Abweichungen von der Normalverteilung ab einer Gruppengröße von 10 (siehe z.B. Bortz, Statistik für Human- und Sozialwissenschaftler.
Nach Friedman würde man als Post Hoc Test z.B. den Wilcoxon nehmen.
Schöne Grüße
Daniela
Hallo Frau Keller!
In meinem Aufbau sind in einem Feld bei mehreren unabhängigen Erhebungen, nach gleichem Muster, mehrere Akteure indentifiziert und ihre Interessen von 0 bis 4, gar kein Interesse bis hohes Interesse, codiert. Es sollen Korrelation und Signifikanz der Interessen aller Akteure hinsichtlich des Ergebnisses in ihrem Feld in drei ordinalen Variablen, also ökonomisch, ökologisch und sozial Resultate, abgeglichen werden.
Dabei scheint mir der Kruskal-Wallis-Test passend zu sein.
Kann ich das in SPSS realisieren ?
Hallo Jens,
ja, den Kruskal-Wallis Test gibt es in SPSS (im Menü z.B. über „Nichtparametrische Verfahren -> Alte Dialogfelder -> k unabhängige Stichproben).
Wegen den ordinalen Variablen würde eventuell auch eine Rangkorrelation oder eine Kreuztabellenanalyse passen.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe zwei unabhängige Stichproben (á n=12). Ich habe jeweils eine Vorher-Nachher Messung durchgeführt. Aus beiden Messergebnissen habe ich die Differenz (Nachher-Vorher) gebildet. Ich habe mit für einen unabhängigen T-Test entschieden. Mir ist aufgefallen, dass die Mittelwerte sich stark unterschieden ( 125 zu 53). Auf den ersten Blick würde man behaupten Gruppe 1 war mit 125 effektiver (hier: Maximalkraft in Newton). Die T-Test Auswertung ergab eine Signifikanz von 0,051 (bei einem Alpha-Fehler von 5%). Als Resultat würde ich behaupten es gibt keinen Signifikanten unterschied zwischen den Gruppen.
Liege ich dort richtig?
Hallo Stefan,
ja, der Unterschied ist nich signifikant, wenn auch nur knapp. Mit einer etwas größeren Stichprobe wäre er signifikant gewesen…
Schöne Grüße
Daniela
Hallo Daniela,
erstmal ein großes Lob für diese Seite und das Skript. Hier spicke ich immer wieder mal ^^ .
Zu dem Thema Normalverteilung habe ich auch eine Frage.
In SPSS gibt es wohl mehrere Möglichkeiten, auf NV zu testen.
Zum einen die „standardmäßige“, die in der Ausgabe Q-Q-Diagramme erstellt und sowohl Kolmogorov-Smirnof als auch Shapiro-Wilk ausgibt; zum anderen aber auch über <Analysieren <Nicht-parametrische Tests <Eine Stichprobe .
Das Ergebnis besagt dann nur "Nullhypothese annehmen/ablehnen" und gibt die Signifikanz und den Mittelwert an.
Die Signifikanz hierbei ist allerdings völlig anders als bei KS.
Bei meinen Daten würde das bedeuten, dass ich in der zweiten Methode wesentlich mehr Werte in NV hätte.
Wie kann das sein? Und welche Methode sollte nun verwendet werden?
Und, eine zweite Frage: Was ist denn die Grenze der Signifikanz für Normalverteilung im KS – 0.05 oder 0.200 ? Ich habe mittlerweile beides mal gefunden….
Ich bin sehr verwirrt und würde mich über eine Antwort freuen 🙂
Liebe Grüße, Miriam
In der Zwischenzeit habe ich rausgefunden, dass das eine die Lilliefors-Korrektur des KS ist, das andere quasi der „normale“ KS. Ich betrachte verschiedene Gruppen, teilweise mit n=150, teilweise auch kleinere Gruppen.
Aber welcher Test auf Normalverteilung sollte wann verwendet werden?
Hallo Miriam,
ich empfehle, sich die Q-Q-Diagramme anzusehen, anstatt sich auf die Normalverteilungstests alleine zu verlassen. Zur Auswahl, welcher Test am besten ist, kann ich keine Empfehlungen geben. Auf folgender Seite gibt es ein paar Hinweise zur Güte der Tests: http://www.bb-sbl.de/tutorial/verteilungen/ueberpruefungnormalverteilung.html
Schöne Grüße
Daniela
Hallo, Frau Keller,
ich stehe vor folgendem Problem und vielleicht können Sie mir helfen: Ich habe zwei Testgruppen, deren Teilnehmer eine Creme in einem bestimmten Zeitraum angewandt haben. Jetzt möchte ich darstellen, ob die Anzahl der Anwendungen (Mittelwerte der Teilnehmer) zwischen den beiden Gruppen sich signifikant unterscheidet. Können Sie mir bitte einen Weg zeigen, wie ich am besten vorgehen sollte, um die p-Werte zu ermitteln?
Vielen Dank im Voraus und herzliche Grüße,
Anne
Hallo Anne,
welche Statistiksoftware verwendest du dazu? SPSS, R, usw. oder Excel, oder ein Online-Tool?
Schöne Grüße
Daniela
Hallo Frau Keller,
zunächst ein Mal ein riesiges Lob an Sie und Ihren Blog! Erstaunlich, wie detailliert Sie auf jeden einzelnen Kommentar eingehen.
Auch ich würde mich gerne mit einer kurzen Frage einreihen:
Wenn ein Teil der Daten logarithmiert werden muss, um eine Normalverteilung zu erlangen, verzerrt dies nicht die Ergebnisse? Anders formuliert: Wenn ich eine Korrelation zwischen zwei Variablen errechnen möchte und eine davon natürlich normalverteilt ist und die andere erst logarithmisch transformiert werden muss, dann ist der errechnete Korrelationskoeffizient doch im Grunde genommen nicht aussagekräftig oder?
Bei meiner Masterarbeit ist genau dieser Fall eingetreten und nun frage ich mich, wie man dies handhaben muss.
Vielen lieben Dank!
Sebastian
Hallo Sebastian,
wenn du Spearman-Korrelationen rechnest, macht es keinen Unterschied, ob auf logtransformierten Daten oder Originaldaten gerechnet wird, da hier nur die Ränge verwendet werden. Bei der Pearson-Korrelation kann schon bei transformierten und nicht-transformierten etwas unterschiedliches heraus kommen. Allerdings erwartet die Pearson-Korrelation einen linearen Zusammenhang. Das heißt, das verlässlichste Ergebnis bekommst du hier, wenn der Zusammenhang einigermaßen linear ist. Das ist oft dann der Fall, wenn die Variablen normalverteilt sind. Wenn eine dafür transformiert wurde und die andere nicht, stört das die Analyse nicht.
Schöne Grüße
Daniela
Wirklich eine super Seite! Ich habe dennoch eine kurze Frage, und zwar: ich habe in einem versuch fische in unterschiedlichen testwässern gehalten und täglich die beschaffenheit der gelegten eier untersucht. Die Eier wurden gezählt und es wurde für jedes Ei festgelegt in welche Kategorie es gehört (zB befruchtet/unbefruchtet etc.). Bei der Auswertung möchte ich nun eigentlich nur wissen ob es für die einzelnen Eiparameter (befruchtet, unbefruchtet…) signifikante Unterschiede zwischen den 6 Treatments gibt. Und wenn ja zwischen welchen. Die Daten sind nicht normalverteilt. Mir wurde gesagt ich soll eine lineare Regression machen, aber das erscheint mir unsinnig/unnötig. Liege ich da falsch? Ich arbeite übrigens mit SPSS 22.
Hallo Elza,
wenn du 6 Gruppen vergleichst und metrische, aber nicht normalverteilte Daten hast, dann brauchst du den Kruskal-Wallis Test. Eine lineare Regression sehe ich hier auch nicht.
Schöne Grüße
Daniela
Hallo Daniela,
tolle Seite hier!
Ich würde mich freuen, wenn du mir auch helfen könntest. Ich möchte meine Daten auf Normalverteilung untersuchen und habe mir dazu schon Histogramme angeschaut, Tests durchgeführt (KS-Test, Shapiro-Wilk) und auch die QQ-Plots. So wie ich es hier nachlesen konnte, empfiehlst du bei größeren Stichproben gerne den QQ-Plot zur Überprüfung. Kann ich den auch nutzen, wenn die meisten meiner Items mittels 5-Punkt-Skalen erhoben wurden? Ich habe dann ja nur 5 Punkte im Plot.
Schon mal besten Dank für deine Antwort!
Josh
Hallo Josh,
ich vermute, es handelt sich bei dir im 5-Punkt Likertskalen. Likertskalen werdne oft wie metrische behandelt, insofern macht auch hier die Prüfung der Normalverteilung mit Q-Q-Diagramm Sinn. Auch bei den 5 Punkten im Plot kann man sehen, ob die schön an der Geraden liegen oder nicht.
Schöne Grüße
Daniela
Hallo, schöne Seite! Eine ganz kurze Frage: Ich suche ein nicht-parametrisches Verfahren um Korrelation (und Signifikanz) mehrere Stichproben zu vergleichen. Gibt es, analog zur multiplen linearen Regression, so etwas wie eine multiple rang-Korrelation (Spearman).
Gruß
Simon
Hallo Simon,
ein wirklich nichtparametrisches Verfahren gibt es nicht. Allerdings müssen für die multiple lineare Regression nicht die Variablen selbst, sondern die Residuen des Modells normalverteilt sein. Das ist also extra zu prüfen und kann auch bei nicht normalverteilten Variablen der Fall sein.
Schöne Grüße
Daniela
Hallo Frau Keller,
ich sitze gerade vor den Daten meiner Masterarbeit und hab da ein Problem. Vielleicht können Sie mir helfen. Und zwar möchte ich ein multiples Modell erstellen um zu testen welchen Einfluss meine unabhängigen Variablen auf meine abhängige Variable haben und wie gut diese die Responsevariable beschreiben. Bei meiner abhängigen Varibale handelt es sich um eine kontinuierliche, die Geldbeträge zwischen 0 und 20 € beschreibt. Die Unabhängigen sind zum Großteil kategorial (Geschlecht, Studienrichtung, Herkunft des Einkommen), jedoch ist auch eine kontinuierliche (Einkommensbetrag) und zwei diskrete Daten (Bildungsabschluss von Mutter und Vater, in Zahlenwerte transformiert) dabei.
Zunächst dachte ich an ein lineares Modell und die Integration der kategorialen Variablen als Dummy-Variablen. Allerdings sind weder meine Daten noch die Residuen normalverteilt. Und Homoscedastizität liegt auch keine vor. Ich hab auch schon versucht die Daten zu transformieren um dadurch Normalverteilung zu erreichen, allerdings war das nicht wirklich erfolgreich.
Haben Sie eine Idee, welches Modell sich anbieten würde oder wie ich Normalverteilung und Homogenität erreichen könnte?
Vielen Dank,
Katharina
Hallo Katharina,
wie hast du die Normalverteilung geprüft? Die Tests auf Normalverteilung sind oft zu streng. Da solltest du lieber Q-Q-Diagramme verwenden.
Ansonsten würde ich noch nach Ausreißern Ausschau halten und die eventuell löschen. Wenn das auch nichts nützt, könntest du das Modell mit Bootstrapping rechnen oder auf ein Multilevel-lineares Modell ausweichen.
Schöne Grüße
Daniela
Hallo Daniela,
ich bin Sportwissenschaftler und habe eine Studie durchgeführt mit eine Versuchsgruppe und einer Kontrollgruppe. Wobei beide Gruppen 8 wochen verschieden Trainiert haben. Es gab ein Pretest und nach 8 Wochen Training ein Posttest. Die Test waren für bei Gruppen gleich.
Nun möchte ich einmal den Pre-und Post Test der Versuchsgruppe vergleichen (gepaarter t-Test) und dann den Post Test von der Versuchsgruppe und der Kontrollgruppe (Mann-Whitney-U Test).
Wäre das so richtig?
Danke
LG
Hallo Mario,
das kommt darauf an, ob die Messwerte normalverteilt sind. Bei Normalverteilung verwendest du für den Pre-Post Vergleich den gepaarten t-Test, ansonsten Wilcoxon. Für den Vergleich zwischen den Gruppen verwendest du bei Normalverteilung den t-Test, ansonsten Mann-Whitney U.
Schöne Grüße
Daniela
Hallo Daniela,
ich beschäftige mich gerade mit der statistischen Auswertung einer klinischen Studie und komme nicht weiter. Ich vergleiche 2 unabhängige Gruppen in Bezug auf Auffälligkeiten in verschiedenen psychologischen Tests.
1. In einem Test möchte ich die Gruppen in Hinischt auf die Merkmale „auffällig“, „grenzwertig“ und „unauffällig“ vergleichen. Ich habe hierfür Kreuztabellen und den Chi-Quadrat-Test verwendet. Diesen kann ich aber leider nicht verwenden, da >20% meiner Zellen Häufigkeiten <5 haben. Gibt es hier Alternativen? Den exakten Test nach Fisher kann ich in SPSS zwar auswählen, darf ich aber laut deiner Ansicht nur für 2×2-Tabellen anwenden? Könnte ich hier auch den Mann-Whitney-Test anwenden?
2. Ich muss noch weitere Tests auf signifikante Unterschiede prüfen. Hier habe ich sowohl T-Werte als auch Rohwerte. Welche Werte nehme ich hier für den t-test bzw. Mann-Whitney-Test? Ein Vergleich der Rohwerte ist ja eigentlich nicht möglich, da z.B. bei einem Intelligenztest die Rohwerte je nach Alter anders interpretiert werden und somit nicht verglichen werden können??
Ganz lieben Dank im Voraus und viele Grüße
Henriette
Hallo Henriette,
die in SPSS über „Exakt“ auswählbare Funktion des Fisher Tests kannst du verwenden, auch für die größere Tabelle. Der „normale“ Fisher Test geht nur bei 2×2-Tabellen und wird auch nur da von SPSS ausgegeben. Alternativ kannst du versuchen, Zellen zusammen zu fassen.
Zu 2: hier verwendest du die T-Werte.
Schöne Grüße
Daniela
Guten Tag Daniela Keller,
einen ganz tollen Blog hast du hier!
Ich hätte bezüglich des u-Tests zwei Fragen an Dich. Im groben geht es um die Bewertung von Bildern. Diese Bilder sind in verschiedene Kategorien einsortiert. Es ist so, dass in einer Kategorie ein Bild oder auch zwei Bilder sein können (mehr nicht).
Diese Bilder wurden bewertet mit „Finde ich ok/finde ich nicht ok“, „Ja, würde ich selber verwenden/Nein würde ich nicht selber verwenden“ (Jeweils codiert mit 1 und 2).
Nun habe ich vor einen u-Test durchzuführen. Wichtig ist mir hier, pro Kategorie einen Unterschied zwischen Frauen und Männern heraus zu bekommen. Dementsprechend sind meine unabhängigen Stichproben die weiblichen Teilnehmer und die männlichen Teilnehmer.
Bei einer Kategorie mit einem Bild, könnte ich die Variable mit den Werten 1 und 2 sowie die Variable Geschlecht einfach mit dem u-Test überprüfen. (?)
Aber wie gehe ich vor, wenn ich eigentlich drei Variablen habe, die ich in den u-Test bringen muss, wie bei den zwei Bildern pro Kategorie. Kann ich die beiden Bildervariablen einfach addieren, oder ist das problematisch, weil meine Werte sich dann zwischen 1-4 bewegen?
Oder bin ich vielleicht auf einem falschen Weg, und müsste jeweils immer nur die ok/nicht ok Angaben aus den Variablen einzeln betrachten? (Aber dann könnte man ja gar keine Ränge mehr bilden?)
Viele Grüße
Isabelle
Hallo Isabelle,
mit den Bewertungen 1/2 hast du nominale Variablen. Deshalb brauchst du hier nicht den U-Test, sondern verwendest eine Kreuztabelle mit Chi-Quadrat-Test. Siehe auch mein E-Book (https://statistik-und-beratung.de/gratis-e-book-statistische-datenanalyse-die-grundlagen/).
Schöne Grüße
Daniela
Schöne Grüße
Daniela
Hallo Daniela,
ich sitze an meiner Master-Thesis und habe eine Frage zur Normalverteilung. Es geht um eine Prä-Post-Studie zur Wirksamkeit eines Trainingsprogramms. Gerade bei dem Test, der signifikant ist, habe ich in der ANCOVA keine Normalverteilung. Jetzt haben wir aber 130 Stichproben. Ich habe gelesen (Bortz), dass bei größeren Stichproben diese Voraussetzung vernachlässig werden kann. Sollte ich trotzdem noch den QQ-Plott benennen, der eine „annähernde“ Normalverteilung“ anzeigt, oder mich nur auf Bortz berufen.
Übrigens: der Shapiro-Wilk ist .000,
Wenn du eine weitere Literaturabgabe dazu, das man die Normalverteilung vernachlässigen kann, hast, wäre ich dir auch sehr dankbar. Der
Vielen Dank und ich freue mich auf deine Antwort.
Gabi
Hallo Gabi,
ja, du kannst dich auf beides beziehen: QQ-Plot sieht normalverteilt aus und die Fallzahl ist groß. Durch die große Fallzahl macht es auch wenig Sinn, sich auf das Shapiro-Wilk-Testergebnis zu verlassen, da der dann einfach zu scharf ist, die Normalverteilung also zu leicht ablehnt. Bortz ist schon gut als Referenz. Dass die Tests auf Normalverteilung bei großer Stichprobe zu scharf sind, steht z.B. auch in Andy Field, Discovering Statistics using SPSS.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe zu dem Thema „Prüfung der Normalverteilung“ auch eine Frage.
Bei mir sieht das QQ-Plot ordentlich aus. Jedoch zeigt das Histogramm, dass meine empirische Verteilung zu steil ist. Das wird auch durch die Kurtosis bestätigt (2,432 bei SE: 0,430). Ich hatte jetzt bspw. in Cramer (1998) gelesen, dass in dieser Konstellation die Hypothese von der Normalverteilung abgelehnt werden kann. Was ist deine Meinung dazu?
Danke für die Unterstützung,
David
Hallo David,
ich halte mich gern an die Q-Q-Plots, da die Tests auf Normalverteilung oft zu streng sind. Allerdings hängt das auch sehr an der Fallzahl, die ziehe ich dazu also auch immer in Betracht.
Schöne Grüße
Daniela
Hallo,
ich hatte diese Frage bereits gestellt, aber mein Kommentar wurde komischerweise nicht veröffentlicht 🙁
Bei mir haben sich mittlerweile einige Fragen gesammelt und ich würde mich über eine kurze Rückmeldung sehr freuen.
1)Ich habe mir für meine AV “Einkommen” ein Histogramm ausgeben lassen und dann gesehen, dass es nicht normalverteilt ist. Also habe ich es logarithmiert. Für den t-test muss auch das logarithmierte Einkommen verwendet werden, liege ich da richtig?
2)Mir leuchtet leider noch nicht ganz ein, was mir der t- bzw. F-Wert sagt und wie ich das logarithmierte Einkommen interpretiere.
Bsp: Für das logarithmierte Einkommen des Mannes habe ich einen Mittelwert von 8,1 und für die Frau 7,6. Der t-wert liegt bei 15,32.
(Muss bei diesen Tests die Spalte „Mean“ überhaupt interpretiert werden?)
3)Die Mittelwert-Vergleiche und damit verbunden der t-Test sind für metrische Variablen gedacht. Welche Tests gibt es denn für dichotome bzw. Dummy-Variablen?
4)Muss ich für jede Variable, die ich in meinen Analysen verwende auf Normalverteilung prüfen? Oder kann ich bei großen Stichproben automatisch von einer Normalverteilung ausgehen?
Vielen Dank im Voraus und liebe Grüße
Hallo Eleo,
1) habe ich dir schon im anderen Kommentar beantwortet.
2) den t-Wert oder F-Wert direkt brauchst du nicht interpretieren. Wichtig für die Interpretation ist der p-Wert, der sagt ob es einen signifikanten Unterschied gibt.
3) willst du den Zusammenhang zwischen zwei kategorialen Variablen untersuchen? Dann ist das ein Chi-Quadrat-Test.
4) Du solltest die Verteilung prüfen. Dabei fallen auch schiefe Verteilungen und Ausreißer auf.
Schöne Grüße
Daniela
Guten Morgen,
erst einmal ein riesen Dankeschön für die guten Erklärungen.
Ich hätte aber noch zwei Fragen…vermutlich stehe ich momentan auf dem Schlauch.
1)Ich habe mir für meine AV „Einkommen“ ein Histogramm ausgeben lassen und dann gesehen, dass es nicht normalverteilt ist. Also habe ich es logarithmiert. Für den t-test muss ich also auch das logarithmierte Einkommen verwenden?
2)Mir leuchtet noch nicht so ganz ein, wie ich die Werte dann interpretiere 🙁
Für das logarithmierte Einkommen des Mannes habe ich einen Mittelwert von 8,1 und für die Frau 7,6. Der t-wert liegt bei 15,32.
Ich würde mich über eine Antwort freuen. Tausend Dank im Voraus!
Hallo Eleo,
zu 1), wenn die logarithmierten Daten dann normalverteilt sind, ja, dann verwendest du die. Allerdings ist das Histogramm nicht gut zur Einschätzung der Verteilung geeignet. Verwende besser Q-Q-Diagramme.
zu 2), du kannst für die Interpretation die Mittelwerte mit der Exponentialfunktion zurücktransformieren. Die Richtung des Unterschieds (Männer haben höheres Einkommen) bleibt aber bestehen, die kannst du also auch so interpretieren.
Schöne Grüße
Daniela
Liebe Daniela,
herzlichen Dank für Deine Antwort.
Ich hatte vorher nochmal einen neuen Kommentar abgeschickt, da ich nicht wusste ob der hier „angekommen“ ist. Dieser kann dann ignoriert werden, da ich die anderen Fragen hier hinein kopiere.
Es haben sich leider noch ein paar andere Fragen ergeben.
zu 2) Wenn ich das logarithmierte Einkommen mit der Exponentialfunktion zurücktransformiere dann habe ich ja wieder meine Ausgangsvariable „Einkommen“, die nicht normalverteilt ist. Und so wie ich das verstanden habe, muss der t-Test mit dem logarithmierten (normalverteilten) Einkommen durchgeführt werden. Und wenn ich das mache, ist mir die Interpretation der Spalte „mean“ etwas unklar. Da es sich hier eben nicht um bspw. 2000Euro handelt sondern um einen Wert von 8,1..
3)Die Mittelwert-Vergleiche und damit verbunden der t-Test sind für metrische Variablen gedacht. Welche Tests gibt es denn für dichotome bzw. Dummy-Variablen?
4)Muss ich für jede Variable, die ich in meinen Analysen verwende (auch für nicht-metrische Variablen) auf Normalverteilung prüfen? Oder kann ich bei großen Stichproben automatisch von einer Normalverteilung ausgehen?
Nochmal vielen Dank und schöne Grüße
Liebe Frau Keller,
ersteinmal ein großes Lob und Dankeschön für Ihre großartige Unterstützung.
Auch ich hätte einige Fragen an Sie und es wäre toll, wenn SIe mir helfen könnten 🙂
Ich untersuche den Einfluss von Barcodescannen auf die Bewertung von Produkten. Hierbei setzt sich die Bewertung in wahrgenommene Qualität, die sich wiederrum in 6 Unterkategorien zusammensetzt (z.B. Herstellung, Stimmung, Gesundheit etc.), wahrgenommen Preis und Kaufabsicht zusammen.
Es handelt sich bei dem Experiment um einen Vorher-Nachher-Vergleich. Die Teilnehmer bewerten das Produkt, scannen dieses, bekommen dann entweder positive oder negative Informationen und bewerten es dann erneut. Die Bewertung erfolgt anhand einer 5-stufigen Likert-Skala (stimme völlig zu – stimme überhaupt nicht zu) und hat insgesamt 30 Fragen. Von diesen 30 Fragen können immer 5 eine der 8 Dimensionen zugeordnet werden. Die Daten wurden Dabei direkt in einem Geschäft, sowie an einer Universität erhoben, an der meistens junge Leute teilgenommen haben. Somit haben Personen, die jünger als 30 Jahre sind, einen Anteil von fast 40%.
So viel zum Aufbau.
Ich habe einige Items des Fragebogens auf Normalverteilung geprüft und die meisten sind nicht normalverteilt. Ebenso habe ich gelesen, dass Likert-Skalen eher als ordinal gelten, auch wenn sie oft wie intervallskalierte Daten verwendet werden.
Aus diesem Grund habe ich mich für den Wilcoxon-Test entschieden, da es sich ja um 2 verbundene Stichproben handelt (vorher-nachher) und habe diesen so angewendet. Mir wurde gesagt, dass ich ruhig auch den T-Test für verbundene Stichprobe wählen kann, da dieser robust sei gegen den Verstoß von normalverteilten Daten. Was denken Sie darüber?
Nun zu einem Beispiel. Wenn ich jetzt folgendes Testen möchte: Negative Informationen über die Herstellung führen zu einer schlechteren Produktbewertung für den Bereich „Herstellung“ und zu einer geringeren Zahlungsbereitschaft“.
Hier habe ich jetzt die 5 Items, die zu dem Bereich „Herstellung“ oder „Preis“ zählen, zusammengefasst und als Mittelwerte in „vorher“ und „nachher“ unterteilt. Dann habe ich den Wilcoxon-Test für „vorher“ gegen „nachher“ angewendet und erhalte auch signifikante Ergebnisse, die meinen Eindruck der Daten bestätigen. Ist das Vorgehen in Ihren Augen richtig?
Nun hätte ich noch 2 Fragen:
wenn ich nun die Gruppen „Studenten“ gegen die im Supermarkt befragten Personen testen möchte: Vergleiche ich nun die Differenzwerte (nachher-vorher) für beide Gruppen gegeneinander? Die Stichprobe wäre damit nicht mehr verbunden, sonden unabhängig, oder? Würde ich hier nun den „Mann-Whitney-U Test“ anwenden?
Und eine letzte Frage: Wenn ich nun bspw. den Einfluss demografischer Daten testen möchte, was bietet sich hier an? Ich möchte herausfinden, demografische Daten wie Bildungsabschluss, Alter, oder Geschlecht einen Einfluss darauf haben, ob sich die Bewertung „vorher“ „nachher“ nach den gezeigten Informationen ändert. Hier habe ich überhaupt keine Idee, wie ich das testen kann.
Es wäre wirklich super, wenn Sie mir behilflich sein könnten.
Vielen Dank und viele Grüße
Michael 🙂
Hallo Michael,
ja, der t-Test gilt als robust auf Verletzungen der Normalverteilung, wenn die Stichprobe groß ist.
Dein Vorgehen ist richtig.
Beim Vergleich der DIfferenzwerte zwischen den beiden Gruppen brauchst du den Mann-Whitney U Test, also auch richtig.
Für den Einfluss weiterer Faktoren benötigst du ein komplexeres Modell, z.B. eine ANOVA oder Regression.
Schöne Grüße
Daniela
Liebe Frau Keller,
vielen Dank für Ihre Antwort. Das freut mich sehr, dass ich hier auf dem richtigen Weg bin 🙂
Viele Grüße
Michael
Liebe Frau Keller,
ich hätte nochmal eine Frage an Sie und es wäre super, wenn Sie mir nochmal kurz helfen könnten.
Ich hatte ja oben bereits erwähnt, dass ich non-parametrische Tests anwenden muss und dass ich die Unterschiede innerhalb der Faktoren bspw. „Gesundheit, vorher-nachher)“, „Stimmung, vorher-nachher)pro Faktor anhand einesWilcoxon-Tests teste, was Sie als korrekt eingstuft haben.
Den Vergleich der Bewertung der Gruppen „Studenten“ vs „Renter“ z.B. anhand eines Mann-Whitney Tests.
Wie sieht es nun aus, wenn ich testen möchte, ob Informationen den Faktor „Gesundheit“ stärker beeinflusst haben als den Faktor „Stimmung“? Wenn ich mir die Differenzwerte (vorher-nachher) für die Faktoren anschaue, sprechen die eine klare Sprache. Diese sind beim Faktor Gesundheit doppelt so hoch.
Mit welchem Test kann ich dies aber denn statistisch belegen?
Über Ihre Hilfe wäre ich sehr dankbar 🙂
VG
Michael
Hallo Michael,
kannst du diese Differenzen (oder eventuell die prozentualen Differenzen) der beiden Faktoren vergleichen ? Das wäre dann wieder ein Mann-Whitney U Test.
Schöne Grüße
Daniela
Hallo,
vielen lieben Dank für die Antwort.
Ja, das kann und werde ich dann so machen 🙂
VG
Michael
Liebe Frau Keller,
je länger man recherchiert, um so mehr widersprüchliche Aussagen findet man zu folgendem Thema (daher wende ich mich nun ratsuchend an Sie):
Müssen die für eine multiple lineare Regression verwendeten Variablen normalverteilt sein? Dass die Residuen es sein müssen, konnte ich bereits in Erfahrung bringen.
Sollten die Variablen nicht normalverteilt sein müssen, haben Sie u.U. eine zitierfähige Quelle für diese Information?
Besten Dank im Voraus und viele Grüße vom Bodensee 🙂
Ach, das hatte ich vergessen:
Die Variablen sind intervallskaliert.
Hallo Benjamin,
die Variablen an sich müssen nicht normalverteilt sein. Andy Field (Discovering Statistics using SPSS, SAGE, 2013) schreibt dazu auf Seite 311 im Abschnitt über die normalverteilten Residuen: „Some people confuse this assumtion with the idea that predictors have to be normally distributed. In fact, predictors do not need to be normally distributed.“
Schöne Grüße
Daniela
Vielen, vielen Dankfür die Turboantwort! Sie sind die Beste!
🙂
Hallo liebe Frau Keller,
erst einmal ein dickes Lob an Sie, dass Sie sich die Zeit nehmen und dann auch noch so gut erklären.
Ich habe folgendes Anliegen:
Ich habe nun meine Variablen mittels des Shapiro-Wilk-Tests berechnet. Das erschreckende Ergebnis lautete bei keiner meiner Variablen läge eine Normalverteilung vor. Dies war ziemlich ernüchternd. Allerdings habe ich bei der Betrachtung der Q-Q Diagramme (ohne Trendbereinigung) gesehen, dass meine Werte in der Regel ziemlich genau auf der Geraden liegen, dies spricht dann ja für eine Normalverteilung.
Nur bei zwei Variablen existiert der von Ihnen beschriebene Bogen in sehr schwachem Ausmaß. Nun lautet meine Frage, ob es ausreicht nur diese beiden Variablen zu transformieren oder bedarf es der Transformation aller Variablen?
Was wäre denn das nicht parametrische Verfahren für eine Multiple-Regressionsanalyse und eine MANOVA?
Vielen Dank schon mal für die Antwort!!!
Viele Grüße und weiter so!
Katja
Hallo Katja,
wenn die Q-Q-Diagramme gut aussehen, liegt Normalverteilung vor. Wahrscheinlich hast du eine große Stichprobe, da sind die Tests zu streng. Bei den Q-Q-Diagrammen mit Bogen kannst du die Transformation einfach ausprobieren und schauen, ob es besser wird. Es müssen nicht alle transformiert werden.
Für die multiple lineare Regression und die MANOVA gibt es keine nichtparametrische Alternative. In SPSS können zumindest Teilergebnisse der beiden mit Bootstrap berechnet werden. Die sind dann auch bei nichterfüllten Voraussetzungen verlässlich.
Allerdings ist für die multiple lineare Regression z.B. gar nicht die Normalverteilung der Variablen gefordert, sondern die Normalverteilung der Residuen. Die hast du wahrscheinlich noch gar nicht angesehen, oder?
Schöne Grüße
Daniela
Hallo! 🙂 Ich muss in 4 Tagen meiner Bachelorarbeit abgeben und bin verzweifelt. Ich bin überglücklich, dass es deine Seite gibt! Wirklich toll!
Mein Problem:
Ich habe an zwei Gruppen eine pychologische Testskala zur Ermittlung der Selbstwirksamkeit durchgeführt. Meine Daten sind nicht normalverteilt, besitzen keine Varianzhomogenität. Ich möchte daher den U-Test nach Mann & Whitney nehmen, um zu schauen, ob sich die Gruppen signifikant voneinander unterscheiden.
Ich habe für jede Gruppe die Testwerte anhand des Manuals ausgewertet. Ich habe jetzt jeweils einen Testrohwert für jede Gruppe (alle Testwerte aufaddiert und durch die Anzahl der Gruppe geteilt). Diese Rohwerte werden anhand von Normtabellen in T-Werte überführt und Prozentränge sind da auch zu finden.
Welche Werte muss ich für die beiden Gruppen mit dem U-Test vergleichen? Nehme ich dazu die Rohwerte? Oder die normierten T-Werte?
VIELEN DANK! 😀
Hallo Luise,
es müsste mit beiden (roh und normiert) das gleiche Ergebnis beim U-Test herauskommen.
Schöne Grüße
Daniela
Kann es daran liegen: die unabhängige Variable (wurde so differenziert „Ja“, „Nein“) genau bei jeweils „Ja“ und „Nein“ 22 Nennungen hat. Soll ich trotzdem U-Test machen, auch wenn Median gleich ist und nur mit den Rängen argumentieren. Oder soll ich in dem Fall gar kein U-Test machen?
Du kannst den Test schon machen, da du ja die Signifikanz wissen möchtest. Am besten du gibst beides an, Mediane und Ränge. Und diskutierst bei den Ergebnissen diesen Sonderfall.
Liebe Daniela,
vielen vielen Dank für deine Hilfe!
Kann es sein, dass mit U-Test sich eine Signifikanz ergibt, den Median ist aber bei den beiden Gruppen gleich ist? Und wie kann es überhaupt interpretiert werden?
Danke!!!
Hallo Katerina,
ja, das kann passieren, da der U-Test mit den Rängen und nicht mit dem Median rechnet. Für die Interpretation ist der Median aber besser. In dem Fall natürlich unpraktisch 😉 Dann also doch mit den Rängen argumentieren. Der Unterschied ist wahrscheinlich aber nicht extrem und die Fallzahl groß, oder? Bei großer Fallzahl wird der Test nämlich auch signifikant, obwohl der Unterschied klein ist…
Schöne Grüße
Daniela
Hallo Daniela,
ich möchte Mann-Whitney-U-Test für zwei unabhängige Stichproben (SPSS) durchführen. Kann man den Test durchführen, wenn die abhängige Stichprobe solche Ausprägungen hat: „stimme voll und ganz zu“ „stimme eher zu“ „stimme eher nicht zu“ und „stimme gar nicht zu“? Meine Daten sich nicht normalverteilt.
Vielen Dank!
Anhängige Stichprobe besteht aus zwei Gruppen (n=29) und (n=10).
Hallo,
das sind Likert-Skalen. Und ja, dafür passt der Mann-Whitney U Test.
Schöne Grüße
Daniela
Liebe Daniela,
vielen lieben Dank für die schnelle Antwort! Hätten Sie vielleicht Vorgaben, wie Mann-Whitney U Test im Text beschrieben/argumentiert werden soll? Welche Angaben müssen auf jeden Fall im Text stehen?
Reicht es, wenn man nur den mittleren Rang angibt und damit argumentiert? Haben das Sie vielleicht schon auf Ihrer Seite erklärt?
Vielen vielen Dank und schönen Tag!
Katerina
Hallo Katerina,
das Ergebnis des Mann-Whitney U Tests wird mit der Teststatistik (U oder Z), der Fallzahl und dem p-Wert angegeben. Zur Beschreibung der Richtung des Unterschieds kannst du mit den Rängen arbeiten, oft ist es aber einfacher, den Median zu verwenden, da der einfacher zu interpretieren ist. Grundsäztlich lohnt es sich, nach den APA-Styles zu schauen, wie dort empfohlen wird, die Testergebnisse anzugeben.
Schöne Grüße
Daniela
Hallo Frau Keller,
meine Frage ist folgende: Wenn ich eine normalverteilte AV und eine nicht normalverteilte UV habe, muss ich dann für die Korrelation Pearson, oder Spearman verwenden?
Danke im Voraus für Ihre Hilfe
Hallo,
sobald eine Variable nicht normalverteilt ist, nimmst du Spearman.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe Daten, die nicht normalverteilt sind, sondern eine negative Schiefe aufweisen. Daraufhin habe ich es mit einer log Transformation versucht und die Daten sind jetzt aufgrund der Transformation normalverteilt. Aufgrund der negativen Schiefe musste ich die Werte bei der Transformation umdrehen. Kann ich mit den lognormalverteilten Daten jetzt einfach so weiter rechnen, z.B. eine Anova, oder muss ich noch etwas beachten? Vielen Dank schon mal!
Liebe Grüße,
Martin
Hallo Martin,
mit den transformierten Werten kannst du nun so weiterrechnen. Wenn du deskriptive Werte aus der weiteren Analyse (z.B. die automatische Berechnung der Mittelwerte bei der ANOVA in SPSS) verwendest, musst du allerdings bei der Interpretation an die geänderte Skala denken.
Schöne Grüße
Daniela
Hallo!
Ich schreibe meine Bachelorarbeit und möchte eine Moderation mit dem Process Macro von Hayes überprüfen. Wie ich verstehe, die Normalverteilung der Residuen muss ich nicht nachweisen, allerdings die Heteroskedastizität und die Unabhängigkeit, richtig? Was sonst muss ich beachten? Die andere Frage ist, wie man die ideale Größe der Stichprobe mit g*power für einen Hayes Test bestimmen kann – welchen Test muss man wählen? Danke mehrmals im Voraus!!!
Hallo Katharina,
wieso sollte die Normalverteilung nicht geprüft werden? Meiner Ansicht nach müssen alle Voraussetzungen wie bei der Regression gegeben sein.
Für die Moderations- oder Mediator-Analyse gibt es meines Wissens nach keine Fallzahlplanung in G*Power.
Schöne Grüße
Daniela
Hallo Frau Keller,
ihr Blog ist wirklich super und ich hoffe, dass Sie auch mir helfen können:
Ich habe eine große Stichprobe. Meine Outcome-Variable (Belastungsscore) ist metrisch skaliert und normalverteilt. Nun möchte ich T-Test durchführen, um zu sehen, ob zwischen Männer und Frauen Mittelwertunterschiede im Bezug auf die Belastung vorliegen, bzw. zwischen den Altersgruppen, zw. Erwerbsstätigen und Nicht-Erwerbstätigen usw. Damit ich T-Tests durchführen kann, müssen die Werte normalverteilt sein, reicht es nun aus, wenn die Werte der Outcome-Varibale normalverteilt sind, oder muss ich nun auch für jede einzelne Kategorie der unabhängigen Variablen (also Männer, Frauen, U30, Ü30 usw), die ich vergleichen möchte, vorher prüfen, ob sie im Bezug auf die Outcome-Variable normalverteilt sind, bevor ich den T-Test durchführen kann? Also beispielsweise ist die Belastung unter den Männern normalverteilt, als auch unter den Frauen usw.
Vielen Dank für die Antwort!!
Hallo Martha,
ja, die Outcome-Variable muss für jede untersuchte Gruppe einzeln normalverteilt sein.
Schöne Grüße
Daniela Keller
Hallo und vielen Dank für die guten Erklärungen!!
Ich hoffe, Sie können mir auch weiterhelfen. Ich habe folgendes Problem:
Ich habe eine ziemlich große Stichprobe mit über 9.000 Fällen, der Kolmogrovo S. Test gibt mir ein Sig.niveau von .000 an, also nicht normalverteilt…
Das Histogramm und das Normalverteilte Q-Q-Diagramm sehen aber schon nach einer Normalverteilung aus… (höchstens kleine Ausreißer am Anfang und Ende). Was kann ich noch tun, um es zu testen?
Habe die Werte schon neu berechnet (Lg10), aber das hat nicht geholfen.
Kann ich den T-Test trotzdem durchführen oder sollte ich dann besser auf den M.W-Test ausweichen? 🙁
Hallo Sonja,
dass der KS-Test hier signifikant ist liegt daran, dass die Stichprobe so groß ist. Da erkennt er auch eine minimale Abweichung von der Normalverteilung als signifikant. Im Gegenzug sind aber die parametrischen Methoden robust auf Abweichugnen von der Normalverteilung, wenn die Stichprobe groß ist. Du kannst also getrost den t-Test verwenden und dich auf die Einschätzung der Normalverteilung mittels Q-Q-Diagramm stützen.
Schöne Grüße
Daniela
Hallo Frau Keller,
ich bin gerade auf Ihren super Blog gestoßen und habe schon einige hilfreiche Einträge gesehen und mich über die verständlichen Erklärungen gefreut!
Jedoch habe ich noch eine ungeklärte Frage bezüglich der Datenauswertung, welche ich gerade durchführe. Ich vergleiche zwei unabhängige Stichproben und möchte untersuchen, ob diese sich im Alter signifikant unterscheiden. Das Alter ist in beiden Stichproben (N=110, N=180) nicht normalverteilt, so machen in beiden Fällen 18-35-jährige Personen ca. 80% der Stichprobe aus und weder die grafische (P-P-Plot, Boxplot, Histogramm), noch die Testung (KS) oder die deskriptive (Kurtosis,Schiefe, Median, Modus, Mittelwert) Betrachtung spricht für Normalverteilung. Ist es demnach richtig, nicht mit einem t-Test, sondern mit einem Mann-Whitney-U-Test als nonparametrisches Verfahren auf bedeutsame Unterschiede im Alter zwischen den Stichproben zu testen? Ich würde mich sehr über eine Antwort von Ihnen freuen, da ich gerade total verunsichert bin.
Vielen Dank Ihnen im Voraus!
Ja, so ist es!
Schöne Grüße
Daniela Keller
Vielen Dank Ihnen für die schnelle und hilfreiche Antwort!
Ich war u.a. auch etwas verunsichert, da SPSS ein U von 10109,5 ausgibt bei mittleren Rängen von 159 und 145 bzw. Rangsummen über 30000 und 16000 und ich über die hohen Zahlen erst verwundert war. Diese sind aber vermutlich darin begründet, dass ich, wenn auch sehr wenige, Teilnehmer bis zu einem Alter von 78 Jahren dabei habe.
Vielen Dank Ihnen, Frau Keller!
Guten Tag Frau Keller,
ich habe auch ein Problem hinsichtlich der Testauswahl. Ich habe 2 Gruppen von Probanden ( Gesund und Krank) bei denen ich einmal ein Merkmal im Blut messe. Die Probanden sind alters-und geschlechtsgepaart. Also Gesund 1 hat das gleiche Geschlecht und das gleiche Alter wie Krank 1. Kann ich hierfür einen Paired t-Test anwenden, um zu prüfen, ob sich die mittlere Differenz der Messwerte unterscheidet? Hierfür ist eine Normalverteilung vorausgesetzt. Zur Überprüfung verwende ich den Kolmogorov-Smirnov Test. Falls keine Normalverteilung vorliegt kann ich den Wilcoxon Paarvergleichstest anwenden? Liegen hier abhängige (alters-und geschlechtsgepaart) oder unabhängige Stichproben vor?
Vielen Dank für Ihre Hilfe.
Hallo Lars, da es sich um gematchte Stichproben handelt, sind es verbundene Messwerte, deshalb ist dein Vorschlag richtig: gepaarter t-Test bzw. Wilcoxon Paarvergleichstest.
Schöne Grüße
Daniela
Guten Tag Frau Keller
Besten Dank für Ihre Ausführungen.
Ich habe eine Stichprobe von 300 Personen und verschiedene Gesundheitsvariablen, welche ich auf ihre Zusammenhänge hin untersuchen möchte. Also z.B. geht X mit erhöhter Y einher? usw.
Jetzt sind alle Variablen bis auf eine nicht normalverteilt. Da es sich um eine „gesunde“ Stichprobe handelt, haben wir viele kleine Werte, die Verteilung ist also schief.
Ich habe versucht die Daten zu logaritmieren, dies hat aber leider nicht geklappt. Mit dem kolmogorov smirnov Test sind sie immer noch nicht-normalverteilt. Gibt es nebst dem logaritmieren andere Möglichkeiten die Daten „parametrische-Verfahrens-gerecht“ zu machen? Ich könnte Spearman-korrelationen rechnen, aber ich wollte auf bestimmte Variablen kontrollieren (Alter) und dies geht nur mit Pearson im SPSS?
Dann habe ich ein weitere Frage im Fields habe ich gelesen, dass bei so grossen Stichproben das zentrale Grenztheorem zum tragen kommt und somit die Stichprobenverteilung unabhängig von der Verteilung der Variablenausprägung in der Population
als normalverteilt betrachtet werden kann? Kann ich also trotzdem parametrische Verfahren rechnen? Wie sehen Sie das?
Besten Dank für Ihre Antwort.
Gruss Anita.
Hallo Anita,
es gibt noch weitere Transformationen, die du ausprobieren könntest (z.B. 1/x, Wurzel(x) usw). Und es stimmt, bei großen Stichproben ist die Abweichung von der Normalverteilung nicht so schlimm. Und es stimmt auch: Die Partialkorrelation (Korrelation mit Kontrolle für eine dritte Variable) basiert auf der Pearson-Korrelation.
Noch ein Hinweis: der Kolmogorov-Smirnoff Test (und auch die anderen Tests auf Normalverteilung) sind zu streng bei so einer großen Stichprobe. Deshalb die Verteilung besser mit Q-Q-Diagrammen prüfen!
Schöne Grüße
Daniela
Hallo Frau Keller,
ich bin gerade leider etwas überfordert und hoffe sehr, dass Sie mir helfen können. Ich habe ein Experiment mit einem between-subject design (12 Gruppen) durchgeführt. Nun will ich die Ergebnisse analysieren. Ich habe eine unabhängige Variable (ordinal Niveau), mehrere abhängige Variablen (interval und ordinal Niveau) und mehrere Mediatoren (interval, ordinal und nominal Niveau). In welchem Test kann ich all diese Variablen unterbringen? Oder gibt es da mehrere Tests, die ich nacheinander durchführen muss?
Hallo Kim,
welcher Test passt, hängt nicht nur an der Art der Daten, sondern auch an der Hypothese/Fragestellung. Also, wie ist die Fragestellung, die du mit der Analyse beantworten willst?
Schöne Grüße
Daniela
Hallo Daniela,
es handelt sich um unverbundene Stichproben und es geht um die Unterschiede zwischen den einzelnen Probandengruppen. Dabei interessiert mich auch, zwischen welchen Gruppen sich genau die (signifikanten) Unterschiede befinden.
In der Studie habe ich eine Produktempfehlung auf verschiedene Arten präsentiert und die Teilnehmer anschließend nach Akzeptanz, Glaubwürdigkeit etc. der Empfehlung und Meinung, Einstellung, etc. gegenüber dem Produkt gefragt. Zudem wurde für bestimmte Mediatoren kontrolliert, z.B. ob die Probanden das empfohlene Produkt vorher schon kannten.
Ich freue mich auf deine Antwort!
Schöne Grüße
Kim
kleiner Nachtrag: in den Gruppen befinden sich 30 bis 60 Personen.
Hallo Kim,
also sind Akzeptanz, Glaubwürdigkeit usw. die abhängigen Variablen? Und die Art der Präsentation ist die unabhängige Variable (Gruppen)? Wenn ja, wie viele Gruppen gibt es?
Schöne Grüße
Daniela
Hallo,
ich hätte da mal eine wahrscheinlich dumme Frage..
Wenn ich eine Anzahl von Objekten getestet habe auf Reaktion ja oder nein, welchen Test kann ich denn anwenden, um statistisch festzustellen, ob es in dieser einen Runde einen signifikanten Unterschied zwischen ja und nein gibt? Wenn ich ein Histogramm erstelle, ist klar ein Unterschied zu erkennen, aber eine Grafik ist ja kein statistischer Test..
Des Weiteren habe ich die Art der Reaktion beobachtet (also kategoriale Daten mit 4 Möglichkeiten) und möchte nun wissen, ob diese von einer weiteren kategorialen Variable abhängen (Richtung, also auch 4 Möglichkeiten). Kann ich dafür einen Chi²-/Fisher-Test anwenden?
Viele Grüße
Hallo,
zur ersten Frage: du kannst mit einem Binomialtest prüfen, ob der Anteil von „ja“ signifikant von 0,5 unterschiedlich ist.
zur zweiten Frage: da geht der Chi-QUadrat-TEst (Fisher geht nur bei 2×2-Tabellen).
Schöne Grüße
Daniela
Liebe Frau Keller,
ich möchte mich den Fragen anschliessen. Ich bin etwas verunsichert was die Normalverteilung angeht. Ich möchte einen T-Test und eine Anova durchführen. Ich dachte zunächst ich müsste die Normalverteilung für die einzelnen Gruppen in SPSS überprüfen (Explorative Datenanalyse–> Test auf Normalverteilung). Hier werden mir ja der KS und der SW Test ausgegeben. Nun meinte meine Betreuerin es wäre falsch dies für die Gruppen zu untersuchen sondern das müsste für die Gesamte Variable betrachtet werden. In SPSS unter nicht Nicht Parametrische Test, Alte Dialogfelder KS Test. Hier erzielen meine Variablen alle Werte < 0,05 bei der Assymptotischen Signifikanz. Darf ich dann den T-Test und die Anova nicht anwenden oder ist der Test der Gruppen zu betrachten? Vielen Danke schon Vorab Liebe Grüße
Hallo Lisa,
das ist nicht richtig. Die Normalverteilung muss für die Gruppen getrennt geprüft werden, wie du das zuvor hattest.
Im übrigen sind die Tests zu streng. Deshalb sieh dir am besten auch die Q-Q-Diagramme an. Die sind besser zur Einschätzung der Normalverteilung, vor allem, wenn die Stichprobe groß ist.
Schöne Grüße
Daniela
Hallo Frau Keller,
in meiner Bachelorarbeit untersuche ich verschiedene Wasserproben (Grundwasser,Niederschlag, Bodenwasser, Bachwasser und Pflanzen) nach deren isotopischen Zusammensetzung und möchte diese vergleichen, damit ich den Wasserfluss durch den Kreislauf dokumentieren kann.
Da ich bestimmte Werte erst durch eine Extraktion im Labor bekommen habe, musste ich zuerst eine Regressionssanalyse machen, um einen Zusammenhang zwischen Gewichtsverlust und den Isotopwerten auszuschließen.
Nun hatte ich vor t-Tests anzuwenden, jedoch sind nicht alle meine Gruppen normal verteilt. Ich hatte zur Prüfung den KS-Test, Histogramme und QQ-Diagramme verwendet. Den KS Test habe ich für die Isotope des Wasser ( 2H und 18O) jeweils getrennt untersucht, nun kommt es aber vor das von ein und der selben Wasserprobe die 2H-Werte normal verteilt sind, aber die 18O-Werte hingegen nicht. Also schließe ich richtig das ich ein nicht parametrischen Test wie den Mann-Whitney-U Test oder Kruskal-Wallis-Test nehmen soll?
Übrigens sind auch die Stichproben sehr unterschiedlich ( Bodenproben sind nach 4 Samplepoints geteilt mit jeweils N= 52; Grundwasser N=6 ; Niederschläge N=14 ; Pflanzen N=16 )
Schöne Grüße und vielen Dank
Thorsten
Hallo Thorsten,
ja, dann nimmst du nichtparametrische Methoden. Die sind auch bei NOrmalverteilung erlaubt. Es macht also nichts, dass manche Gruppen normalverteilt sind.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe eine Frage zur Effektstärkenberechnung bei nicht normal verteilten Daten: die Formel ist ja r=z/Wurzel N. Ist es richtig, dass N in dem Fall die Summe aus den Fallzahlen beider Stichproben ist? Also bei Prä-Post-Design zweimal die Stichprobe?
Und dann wollte ich noch fragen, ob ich trotz nicht normalverteilter Daten in den Diagrammen Mittelwert und Standardfehler verwenden darf? Oder muss ich Boxplots verwenden?
Vielen Dank
Aurelia
Hallo Aurelia,
ja, das ist dann zweimal die Stichprobe, also die Anzahl der Beobachtungen.
Bei nicht normalverteilten Daten passt der Boxplot besser. Allerdings sieht der Mittelwert mit Standardfehler manchmal übersichtlicher aus. Du musst berücksichtigen, dass der Mittelwert und Standardfehler deine Daten eventuell nicht richtig darstellen, vor allem dann, wenn sie schief sind. Sieh dir einfach beide Bilder an und kontrolliere, ob durch den Mittelwert-Plot der gleiche Eindruck entsteht wie durch die Boxplots.
Schöne Grüße
Daniela
Oder kann ich einfach pro Proband die Gesamtanzahl der Fehler und die Gesamtdauer berechnen und diese auf Normalverteilung prüfen? Vielen Dank für die Hilef
Hallo Laura,
jeder Messzeitpunkt muss für jede Gruppe einzeln normalverteilt sein, wenn du auch in der Analyse diese Messwiederholungen verwendest. Wenn du in der Analyse den Gesamtwert verwendest, muss der für jede Gruppe normalverteilt sein. Wenn du das mit Normalverteilungstests überprüfst, kannst du bei nicht signifikanten Werten von Normalverteilung ausgehen. Allerdings sind die Tests bei größeren Stichproben sehr streng. Deshalb solltest du auf jeden Fall auch Q-Q-Diagramme ansehen.
Schöne Grüße
Daniela
Hallo Daniela, bei meiner Studie wurden zu 4 Testzeitpunkten bei 2 Verschiedenen Aufgaben die Parameter Zeit und Genauigkeit erhoben, außerdem wurden die Probanden in 4 Stimulationsgruppen unterteilt, die es jetzt gilt zu vergleichen. Ich mache eine zweifaktorielle Varianzanalyse mit vierfacher Messwiederholung. bin mittlerweile total verwirrt… welche Daten muss ich jetzt genau auf Normalverteilung untersuchen? nur die baseline-erhegung oder alle Daten? und was ist wenn ein wert nicht signifikant wird?
Danke 🙂
Hallo Daniela,
ich bin Statistiklaie und frage mich bei manchen Verfahren, warum bestimmte Voraussetzungen notwendig sind. Z.B. lese ich desöfteren, dass für einen T-Test eine Normalverteilung der Daten notwenig sei, damit der Test unbedenklich durchgeführt werden kann, d.h. wohl die Testergebnisse somit „stabil“ seien.
Was bedeutet aber dieses „stabil“/unanfällig – ab wann wäre er denn nicht stabil? Warum ist die Normalverteilung eine Voraussetzung für den Test -was wird dadurch sichergestellt?
Vielen Dank für Deine Antwort!
Beste Grüße,
Norman
Hallo Norman,
die Normalverteilung ist eine bestimmte Verteilungsart und hat nichts mit Stabilität zu tun, siehe hier: http://de.wikipedia.org/wiki/Normalverteilung. Überprüfen kannst du sie z.B. mit Q-Q-Diagrammen oder mit Tests auf Normalverteilung. Einige Tests (die parametrischen Verfahren) gehen davon aus, dass die Daten normalverteilt sind und berechnen die Verteilung ihrer Teststatistiken basierend auf dieser Annahme. Diese Tests sind demnach nur gültig, wenn diese Voraussetzung erfüllt ist.
Schöne Grüße
Daniela
Hallo liebe Helfer und Heflerinnen,
ich muss für meine Bachelorarbeit einige Daten mit SPSS auswerten, habe mit Statistik allgemein leider nicht die größte Erfahrung. Die zu untersuchenden Daten sind intervallskaliert, die Varianzen sind homogen, nur besteht keine Normalverteilung der aVs. Wird im diesen Fall ein parametrisches Verfahren angewandt, da ja nur eine Voraussetzung für eine ANOVA verletzt ist, oder muss bei Verletzung der Normalverteilung ein nonparametricher Test gerechnet werden?
Vielen Dank im vorraus!
L
Hallo Leonie,
streng genommen solltest du ein nichtparametrisches Verfahren nehmen. Und wenn du nur einen Gruppenfaktor hast (kein mehrfaktorielles Modell) gibt es hier ja auch super Alternativen. Wenn du doch die ANOVA verwenden willst, kannst du versuchen, über Transformationen eine Normalverteilung zu erzeugen. Wenn du genügend Beobachtungen hast, kannst du dich außedem darauf berufen, dass die ANOVA bei großer Stichprobe robust auf die Verletzungen der Normalverteilung reagiert.
Schöne Grüße
Daniela
Liebe Daniela,
ich frage mich, wie ich Daten im Boxplot oder einem Korrelationsdiagramm darstelle, die ich für das Durchführen eines parametrischen Tests erst transformieren musste (per Box-Cox-Transformation). Plotte ich die originalen (untransformierten) oder die transformierten Daten? Falls die originalen korrekt sind (was ich optisch ansprechender aber irgendwie unlogisch finde): gebe ich trotzdem den p-Wert des Tests an, den ich mit den transformierten Daten durchgeführt habe?
Vielen Dank,
Simon
Hallo Simon,
als Darstellung würde ich das nehmen, was schöner anzusehen ist. Oft ist es so, dass die nicht transformierten Werte so gestaucht sind, dass man nicht gut Unterschiede erkennt. Wenn das mit den transformierten besser aussieht, würde ich die nehmen. Der Nachteil ist, dass sich die Höhe dann nicht wirklich anhand der Skala interpretieren lässt. Ein Kompromiss ist es, wenn man die Originaldaten verwendet und die Skala transformiert (was aber nur bei einfachen Transformationen wie z.B. Log einfach umzusetzen ist). Den p-Wert des Tests der transformierten Daten kannst du immer angeben, der gilt immer. Es wird ja im Text ersichtlich sein, dass der Test auf transformierten Daten gerechnet wurden.
Schöne Grüße
Daniela
Und welchen Korrelationstest nehme ich, wenn ich bei nicht-normalverteilten Daten eine Korrelation zwischen einer kategorialen Variable X (5 Ausprägungen) und einer dichtomen Variable Y (kontinuierliche Variable wurde dichotomisiert) berechnen möchte?
Lg Philippa
Hallo Philippa,
der Zusammenhang zwischen einer kategorialen und einer dichotomen Variablen wird mit Kreuztabellen und z.B. einem Chi-Quadrat-Test überprüft.
Schöne Grüße
Daniela
Hallo liebe Daniela,
vielen Dank für diesen tollen Blog! Auch ich habe eine Frage und wäre dankbarr, wenn du Tipps geben könntest. Zu meiner Studie:
In der Umfrage bewerteten die Teilnehmer (n=90) ein von ihnen genutztes System. Sie bewerteten über 100 Items, die verschiedenen Indikatoren und Dimensionen zugeordnet waren, z.B. der Aufbau für eine der Dimensionen:
Dimension „Systemeigenschaften“
Indikator X „Funktionen“: Item x1, Item x2, Item x3
Indikator Y „Design“: Item y1, Item y2, Item y3, Item y4, Item y5
Indikator Z „Datenintegrität“: Item z1, Item z2, Item z3, Item z4, Item z5, Item z6
Die Skala bildete eine 6-stufige Likert-Skala (Forced Choice).
Meine Gedanken hierzu: auch wenn es durchaus verschiedene Meinungen gibt, so sind die Ergebnisse einer Likert-Skala ja Ordinaldaten. Zur Berechnung des Mittels eines Items wird daher der Median herangezogen.
Meine erste Frage: Ist es möglich, einen Median für einen Indikator zu berechnen, also einen Wert zu ermitteln, der die durchschnittliche Bewertung des Indikators „Funktionen“ widergibt? Kann man den Median für die Dimensionen berechnen?
Meine zweite Frage: Möchte ich die Korrelationen von Indikatoren berechnen, dann verwende ich in diesem Fall ja Spearman-Rho. Ist es richtig, dass ich hierfür die einzelnen Werte der Items (z.B. Item x1, Item x2, Item x3) addiere und mit der errechneten Summe die Korrelationen vornehme? Könnte ich auf diese Weise auch Korrelationen von Dimensionen berechnen?
Ich wäre wirklich sehr dankbar, wenn du Zeit findest meine Fragen zu beantworten.
Einen lieben Gruß!
Liebe Michaela,
zunächst einmal fällt mir zu deiner Umfrage folgendes ein:
1. Du könntest mit einer Faktorenanalyse überprüfen, ob die Zuordnung der Items zu den Indikatoren und Dimensionen auch laut der erhobenen Daten so passt, wie du sie dir vorgestellt hast.
2. Könntest du die Indikatoren und/oder die Dimensionen auf Reliabilität (z.B. mit cohens kappa) prüfen
(das sind aber nur Vorschläge)
Zu deinen Fragen: Ich würde den Mittelwert verwenden, da du den gut aus mehreren Items bilden kannst. Wenn du, wie weiter unten selbst von dir vorgeschlagen, die Summe berechnest, tust du quasi das selbe: Summe oder Mittelwert für aus mehreren Items bilden ist aus statistischer Sicht das gleiche. Führt auch in der weiteren Analyse um gleichen Ergebnis. Mit diesen Mittelwerte oder Summen kannst du dann weiterrechnen und z.B., wie von dir schon überlegt, Korrelationen rechnen.
Schöne Grüße
Daniela
Liebe Frau Keller,
ich arbeite für meine Diplomarbeit an einem großen Datensatz. Es ist eine SP, die befragt wurde. Es ist kein Gruppenvergleich. Jetzt bin ich unsicher, welche Tests ich verwenden sollte. Die Kontrollvariablen möchte ich auf NV prüfen. Diese entsprechen allen Datenniveuas.
1. Kann ich für metrische Daten den Kolmogoriv Anpassungstest nehmen? für die ordinalen Daten fand ich keinen Test und für die kategorialen den Chi Quadrat -Test.
2. Dann würde ich gern berechnen, wie hoch die Korrelation zwischen den KontrV und dem Kriterium ist. Das Kriterium hat metrisches Datenniveau. Kann ich hier den ProduktMomentKorrK nehmen und für die anderen KV den Punkt-biserialen KK? Allerdings geht der doch nur für bivariate Verteilungen?
Vielen Dank im Voraus!!
EB
Hallo,
zu 1: was genau willst du hier untersuchen? Was ist die zugehörige Fragestellung?
zu 2: ja, bei Normalverteilung nimmst du die Pearson-Korrelation, ansonsten die Spearman (für metrische und ordinale). Die Punkt-Biseriale Korrelation geht bei einer dichotomen und einer metrischen.
Grüße
Daniela
Liebe Frau Keller,
Ich habe für meine MA-Thesis 88 Schüler/innen befragt und möchte Unterschiede herausfinden; die AV sind nicht normalverteilt. Meine Unterschiedshypothesen habe ich durch Mann-Whitney-U getestet. Nun geht es an die Exploration.
Hierfür bilde ich immer wieder neue Gruppen (z.B. nach Variablen Geschlecht, Schulabschluss Eltern, Erfahrungen in der Schule) und führe jeweils Mann-Whitney-U bzw. Kruskal-Wallis-Tests für verschiedene abhängige Variablen mit SPSS durch.
Kann ich überhaupt so vorgehen? Kann ich in der Dokumentation die Signifkanzen/p-Werte miteinander vergleichen?
Ich habe gerade Angst, einen Fehler zu begehen.
Danke für die Hilfe.
Hallo Alexandra,
ja, so kannst du vorgehen. Zum Vergleichen direkt nimmt man die p-Werte nicht. Nur zur Entscheidung signifikant ja/nein. Wenn du die verschiedenen Vergleiche vergleichen willst, könntest du z.B. mit den Effektstärken arbeiten.
Schöne Grüße
Daniela
Vielen Dank , Frau Keller!
In der Facebook-Gruppe wurde diskutiert, ob ich trotz Nicht-Normalverteilung T-Tests und Varianzanalysen durchführen kann. Wenn ich zwei Gruppen bilde, dann jeweils n>30, aber wenn ich (z.B. anhand Variable Schulform) 5 Gruppen bilde, dann n<30 , d.h. nicht-para-Verfahren. Und dann kann ich ja z.B. Kruskal-Wallis und T-Test /Anova nicht miteinander vergleichen, oder? also für alle nicht-parametrische Verfahren?
– Sie empfehlen keine einseitigen Signifikanztests. Sollte ich also (z.b. bei Mann-Whitney-U) auch bei einer gerichteten Hypothese die asymptotische Signifikanz nicht halbieren?
– Welche Möglichkeiten der Berechnung der Effektstärke gibt es z.b. bei Mann-Whitney-U und Kruskal-Wallis? Kann ich die Korrelation (Spearman) zwischen den Variablen als Effetstärke angeben?
Vielen Dank im Voraus und schöne Pfingsten
Alexandra
Hallo Alexandra,
Kruskal-Wallis und ANOVA liefern beide das Ergebnis, ob es einen signifikanten Unterschied gibt oder nicht. Das Ergebnis, signifikant ja/nein, ist in dem Sinn schon vergleichbar. Also kannst du unterschiedliche Verfahren verwenden und musst nicht für alle Vergleiche nichtparametrische nehmen.
Ja, ich würde in den allermeisten Fällen zweiseitig testen, also den p-Wert nicht halbieren.
für Mann-Whitney U wird die Effektstärke aus dem Z-Wert des Testergebnisses berechnet: Effektstärke r=Z/Wurzel(N). Der Z-Wert ist die standardisierte Teststatistik, N ist die Fallzahl. Für den Kruskal-Wallis Test gibt es kein einfach zu berechnendes Effektstärkemaß. Hier kannst du vielleicht auf die Paarvergleiche und dann auf das Ergebns des Mann-Whitney U Tests zurückgreifen?
Schöne Grüße
Daniela
Liebe Frau Keller,
ich habe meine Daten ausgewertet und stehe vor einem Problem:
Aufgrund der Voraussetzungsverletzungen habe ich mehrere Mann-Whitney U Test berechnet, bei dem ein paar Werte signifikant wurden.
ZUm Vergleich habeich trotzdem eine MANOVA und explorativ post-hoc ANOVAS mit alpha Korrektur berechnet.
Im Großen und Ganzen kamen diesselben Ergebnisse heraus, jedoch mit dem Unterschied, dass der U-Test bei einer Variable signifikant wurde, diese Variable aber weder bei der MANOVA noch bei der ANOVA signifikant wurde. Kann das sein? Und wenn ja, welche Gründe könnte es dafür geben?
ich sitze gerade an der Diskussion und weiss nicht, wie ich mit dem Ergebnis umgehen soll.
Danke schon mal herzlich!
Hm, das ist ungewöhnlich, da die MANOVA und ANOVA generell eine größere Teststärke haben als der Mann-Whitney U Test. Kann es an der Fehlerkorrektur liegen? Zur Diskussion: eingentlich sollte man sich abhängig von den Voraussetzungen eine Methode auswählen und deren Ergebnis verwenden und nicht zwei rechnen und zwei berichten…
Schöne Grüße
Daniela
Vielen Dank für die Antwort.
Dass ich zwei verfahren berechne ist mit meiner Betreuerin abgeklärt
Um zu prüfen ob die Ergebnisse wg der Fehlerkorrektur zustande kamen , berechne ich die anovas nochmal ohne Fehlerkorrektur? Kann ich das so machen oder was raten Sie mir? Stehe gerade etwas auf dem Schlauch.
Danke schon mal recht herzlich
Ja, das kannst du so machen und zumindest für die Diskussion als Grundlage nehmen.
Hallo Frau Keller,
ich habe ein paar Fragen und hoffe SIe können mir weiterhelfen.
1) Ich möchte gerichtet aufgestellte Unterschiedshypothesen auf Signifikanz prüfen. Ein fiktives Beispiel: Männliche Beamten sitzen häufiger mehr als 2h täglich vor dem PC als weibliche. Die UV’s sind jeweils dichotom (Geschlecht; Jung-Alt…). Die AV’S sind ordinalskaliert (z.B. Gar nicht vor dem PC – bis zu 2h vor dem PC – mehr als 2h vor dem PC) oder nominalskaliert (z.B. Raucher – Nichtraucher). Wie gehe ich hierbei am besten vor? Versuche ich alles mit demselben Test zu prüfen (Chi-Quadrat?) oder nehme ich dafür unterschiedliche Tests, und falls ja welche sind dafür jeweils am besten geeignet?
2)Auch ist mir nicht ganz klar, wie ich in SPSS vorgehe, damit ich bei ordinalskalierten Variablen nur eine Ausprägung (z.B. mehr als 2h vor dem PC) auf signifikante Unterschiede prüfen kann. Muss ich hierzu die Variablen zunächst in dichotome umcodieren?
3) Es werden wie beschrieben jeweils nur 2 Gruppen auf Unterschiede untersucht. Wie gehe ich idealerweise vor, wenn eine Gruppe deutlich kleiner ist (unter 10% der Stichprobe) als die andere (über 90% der Stichprobe)? Darf damit überhaupt gerechnet werden, wenn eine der beiden Gruppen nur etwa 25 Probanden enthält und die andere über 300? Sollte hier mittels Levene-Test auf Varianzhomogenität geprüft werden? Oder sind die Tests ohne weiteren Zwischenschritt durchzuführen und lediglich in der Interpretation auf diese Problematik zu verweisen?
Vielen Dank im Voraus!
Liebe Grüße
Paul
Hallo Paul,
zu 1) Chi-Quadrat Test oder Fisher, je nach Größe der Kreuztabelle.
zu 2) Ja.
zu 3) Das ist kein Problem. Varianzhomogenität muss nur für die ANOVA überprüft werden, nicht für die Kreuztabellen.
Schöne Grüße
Daniela
Liebe Frau Keller,
ich hätte eine „kleine“ Frage ;-).
Darf ich den Friedman Test auch bei Normalverteilung anwenden oder muss ich die Anova wählen?
Vielen Dank und herzliche Grüße
Hallo Steffi,
Friedman ist auch bei Normalverteilung erlaubt. Hat nur eine etwas kleinere Power.
Schöne Grüße
Daniela
Vielen lieben Dank 🙂
Hallo Daniela,
ich arbeite zurzeit an meiner Masterarbeit und muss unter anderem eine einfache Regressionsanalyse durchführen. Das Problem ist, dass die benötigten Variablen nicht normalverteilt sind (daher Spearman für die Überprüfung der Zusammenhänge) und kein linearer Zusammenhang zwischen allen Variablen besteht. Diese zwei Punkte werden jedoch als Voraussetzung für die Anwendung einer Regressionsanalyse benannt. Haben Sie einen Tipp für mich, wie ich nun weiter vorgehen kann beziehungsweise welche Alternative ich habe?
Vielen Dank im Voraus und liebe Grüße!
Hallo,
eventuell kannst du die Variablen transformieren (log, Wurzel, 1/x…) und damit sowohl Normalverteilung als auch linearen Zusammenhang erzeugen. Im übrigen müssen nicht die Variablen selbst, sondern die Residuen (Fehlerabweichungen im Modell) normalverteilt sein, das lässt sich aber erst im Nachhinein prüfen.
Gruß
Daniela
Hallo Frau Keller,
nur eine kurze Frage:
Ist es zulässig, mittlere Häufigkeiten zu berechnen? Bei mir geht es u.a. um Häufigkeitsauszählungen von beobachtungsdaten. Ich habe in anderen Diplomarbeiten mit ähnlichen themen dass das so gemacht wurde.
Geht denn das? Und wenn ja wie könnte ich das Vorgehen begründen? Habr dazu leider nichts gefunden.
Hallo, du hast die Häufigkeitswerte direkt erhoben? Dann macht es schon Sinn, die mittleren Häufigkeiten anzugeben. Irgendwie musst du sie ja zusammen fassen. Wenn die Verteilung sehr schief ist, passt aber wohl der Median besser. Einfach mal die Verteilung ansehen.
Gruß
Daniela
Hallo Frau Keller,
Ich habe probleme mit der darstellung meiner deskriptiven ergebnisse und hoffe Sie können mir weiter helfen.
Ich habe mehrere abhängige variablen ( insg. 26 variablen, koennen noch zusammen gefasst werden in einmal 8 und einmal 18 variablen) die absolutskaliert sind also kommen ja nur häufigkeitsverteilungen infrage. Ausserdem habe ich eine KG und eine EG. Ich dachte nun an zwei graphiken. Eine auf der die Häufigkeiten
(Absolute Häufigkeit und relative Häufigkeit) der ersten 8 AVn im gruppenvergleich abgebildet sind und das ganze nochmal fuer die anderen 18 AVn.
Leider habe ich noch keine geeignete Darstellungsform gefunden. Was ganz gut pro variable aussieht ist die bevölkerungspyramide ….gibt es sowas auch fuer mehrere variablen. Ich arbeite mit SPSS 22. Haben Sie sonst noch eine idee wie man das ganze gut und übersichtlich darstellen könnte? Ich verzweifle daran gerade….
Danke schon mal:)
Ich würde auf jeden Fall entweder absolute oder relative Häufigkeiten verwenden, nicht beides. Ansonsten ist wohl das gruppierte Balkendiagramm, eventuell auch ein gestapeltes Balkendiagramm, geeignet. Ich glaube in SPSS bekommt man das nicht für mehrere Variablen in eine Abbildung. Eventuell die Häufigkeiten in Excel kopieren und dort darstellen?
Gruß
Daniela
Hallo Frau Keller ,
Ich habe eine kurze Frage.
Ich habe zwei unabhängige Stichproben und mehrere abhängige variablen. Unterschiede habe ich aufgrund der tatsache dass die meisten AVn nicht normalverteilt sind mittels mann Whitney u test untersucht. Jetzt keimt in mir aber die Überlegung ob das richtig war und ich nicht besser mediantests berechnen sollte, da es bei den AVn auch einige ausreisser gibt. Oder wäre es gut beides anzugeben? Zum vergleich habe ich allerdings noch eine manova gerechnet. Wird das dann nicht zuviel , 3 verfahren fuer ein und dieselbe Fragestellung?
Was raten Sie mir?
Herzlichen Dank schon mal.
Nachtrag.
Falls Sie zu den mediantests raten ,muesste ich dann auch die Graphiken ändern?
Fuer die deskriptiven Ergebnisse habe ich mittels histogramme die Mittel werte der AVn dargestellt.
Bei nicht normalverteilten Daten passen Boxplots besser als Mittelwerte.
Hallo,
ich muss Sie nochmal behelligen:)
Bezügloch Boxplots habe ich jetzt hin und her probiert, aber aufgrund der Tatsache, dass ich zwei Stichproben hab und enorm viele AVn, wird das Ganze mit Boxplots extrem unübersichtlich oder eine lange,seitenweise Darstellung einzelner Boxplots.
Ich habe nun überlegt, die Mittelwertdiagramme zu lassen und zusätzlich in einer Tabelle die entsprechenden Mediane aufzuführen, mit der Begründung noch ein komplexeres Bild der Daten zu bekommen und weil der MW sensibel ggü. Ausreißern ist.
Kann ich das so machen bzw. macht das Sinn?
Habe einerseits ein bischen Angst, meine Arbeit mit zu vielen Infos zu überladen, andererseits mich für die „falschen“ Infos zu entscheiden:(
Danke schon mal herzlich!
Hallo,
ja, so kannst du es machen. Wichtig ist, dass die Abbildungen dem Leser helfen. Verwirren sollen sie auf keinen Fall und wenn es zu viele sind, ist auch keinem geholfen.
Schöne Grüße
Daniela
Hallo Nicole, ja, du solltest dich für ein Verfahren entscheiden und dann dieses Ergebnis verwenden. MANOVA braucht multivariate Normalverteilung der Residuen, die hast du wahrscheinlich nicht, wenn die AV nicht normalverteilt waren. Der Mann-Whitney Test passt, auch bei Ausreißern. Der Mediantest hat eine geringere Power und ist deshalb nicht zu empfehlen.
Schöne Grüße
Daniela
Hallo Frau Keller,
ich habe eine Frage zur Prüfung auf Normalverteilung: Ich möchte mehrere UVs (metrisch) und mehrere AVs (metrisch) durch eine kanonische Korrelation untersuchen. Dabei ist laut Bortz/Schuster (2010) eine multivariate Normalverteilung der Daten Voraussetzung.
Die Befragten haben jedoch bei den jeweils aufsteigenden Likert-Skalierung (1-4; 1-5; 1-6: 1-7) überdurchschnittlich hohe Antworten gegeben, sodass der K-S-Test auf Normalverteilung bei allen Variablen signifikant wird. Die Betrachtung der Q-Q-Diagramme hingegen ist nur manchmal von der geschätzten Geraden abweichend.
Meine 1. Frage: Kann ich zur Beurteilung multivariate Normalverteilung die einzelnen univariaten Normalverteilungen betrachten oder muss ich spezielle Koeffizienten wie den von Mardia hinzuziehen?
Und die 2. Frage: Muss ich die Variablen irgendwie logarithmieren oder dergleichen, damit sie normalverteilt sind und ich die kanonische Korrelationsanalyse durchführen kann? Ich frage mich hier, ob unterschiedliche Likert-Skalierungen die Analyse der kanonischen Korrelation überhaupt erlauben (?).
Und eine letzte 3.Frage: Reicht es nicht aus, dass die Residuen normalverteilt sind?
Ich danke im Voraus schon mal für Ihre Antwort!
Désirée
Hallo Désirée,
zu 1: die univariate Untersuchung ist nicht perfekt, aber eine gute Annäherung, da komplexere Methoden oft in der Software nicht zur Verfügung stehen.
zu 2: Ausprobieren!
zu 3: Ja.
Schöne Grüße
Daniela
Hallo, Daniela
Im Rahmen meiner Bachelorthesis (Eiablage Drosophila bei unterschiedlicher Nahrung) muss ich Daten analysieren wobei sich mir das Problem ergibt, dass bei drei der fünf zu untersuchenden Varianten nur „0“ vorkommt und die Daten somit nicht normalverteilt sind. Allerdings ergibt sich wenn nur die beiden anderen Varianten untersucht werden eine Normalveteilung. Kann ich dann diese beiden mit parametrischen Tests untersuchen?
Wenn ich nun allerdings alle 5 Varianten untersuchen will, welchen Test soll ich anwenden? (Kruskal-Wallis?)
Danke für die Hilfe
David
Hallo David,
ja, für den Vergleich der beiden normalvertielten kannst du parametrische Tests verwenden.
In den anderen Fällen, wo es nur Nuller gibt, wird es wohl auch mit dem Kruskal-Wallis-Test schwierig. Könntest du hierzu die Daten mit den normalverteilten WErten in Nuller und Einser umkodieren (also Eiablage ja/nein?) und dann mit den anderen 3, die ja sowieso nur Nuller haben, in einer Kreuztabelle und mit Chi-Quadrat-Test untersuchen?
Schöne Grüße
Daniela
Guten Tag Frau Keller
Ich habe gewisse Fragen zu meinen Stichproben und der Normalverteilung.
Ich untersuche verschiedene Stichproben (3), welche jeweils über mehrere Jahre (15 / 4 / 1) über die gleichen Themen befragt wurden.
1) Wie vergleiche ich die Jahre miteinander? Ist es möglich, die Daten für die selben Variable in SPSS untereinander aufzulisten, wenn mich nur die Durchschnittswerte über die Jahre interessiert?
2) Gewisse Daten sind gemäss KS-Test nicht normalverteilt, der Q-Q-Plot weicht jedoch nicht immens von der Diagonalen ab. Ab wann muss ich mir eingestehen, dass die Daten wirklich nicht normalverteilt sind?
3) Ich möchte die Daten eigentlich anhand einer linearen Regressionsanalyse untersuchen, welchen Test würden Sie mir ansonsten empfehlen?
Vielen Dank für ihre Hilfe!
LG
Hallo,
zu 1) so genau habe ich das Studiendesign noch nicht verstanden. Ist die erste Stichprobe über 15 Jahre, die zweite über 4 und die dritte nur in einem Jahr gemessen? Wollen Sie die Werte der Jahre ansehen, oder reicht ein Durchschnittswert für jede Stichprobe über die entsprechenden Jahre?
zu 2) Das ist eine subjektive Einschätzung. Dazu kann ich ohne das Bild gesehen zu haben nicht viel sagen.
zu 3) Bei der linearen Regression müssen nicht die Variablen an sich, sondern die Residuen normalverteilt sein. Sie können sie also rechnen und im Ergebnis dann die Residuen auf Normalverteilung prüfen. Eventuell sieht das dann gut aus und Sie können die Ergebnisse verwenden.
Schöne Grüße
Daniela Keller
Liebe Frau Keller,
ich hoffe, Sie können mir weiterhelfen.
Ich habe 1 UV (EG und KG), relativ viele AVs (z.B. Fragebogenwerte, bestimmte Phasen einer Mutter-Kind-Interaktion sowohl Häufigkeit als auch Dauer der Phasen….)
Als Kovariate wollte ich das Entwicklungsalter und die bisherige Therapiedauer mituntersuchen, geplant war eigentlich eine MANCOVA.
Nun ist es aber so, dass weder alle Variablen normalverteilt, noch die Varianzen noch die Varianz-Kovarianz-Matrizen homogen sind und bzgl. der Kovariaten waren auch die Voraussetzungen nicht immer erfüllt (homogene Regressionskoeffizienten, Korrelation KV-AVn).
Ich wollte sowohl Gruppenunterschiede bzgl. der AVn prüfen als auch Zusammenhänge zwischen den Fragebogenwerten und den Mutter-Kind-Interaktionsphasen.
Was kann ich denn nun überhaupt rechnen? Weiss gerade gar nicht mehr weiter:(
Meine Stichproben sind gleichgroß, jeweils 21 Probanden.
Vielen Dank schon mal !
LG
Hallo,
folgendes kannst du versuchen:
1. Überlege, ob du deine Fragestellungen auch mit mehreren weniger komplexen Modellen untersuchen kannst. Wenn du sie so weit herunter brechen kannst, dass du nur noch bivariate Zusammenhänge hast (eine abhängige und eine unabhängige) stehen sogar nichtparametrische Methoden zur Verfügung.
2. Wenn du bei komplexen Modellen bleibst, kannst du, um die Voraussetzung der Normalverteilung zu umgehen, Bootstrap verwenden (gibt es z.B. in der Vollversion von SPSS für die ANOVA und die ANCOVA)
3. Bei nicht homogenen Regressionskoeffizienten kannst du es statt der ANCOVA mit einem Multilevel Linearen Modell versuchen.
Schöne Grüße
Daniela
Weiterführende Fragen könnt ihr gern mit mir und den anderen Teilnehmern in der Facebook-Gruppe Statistikfragen diskutieren. Hier der Link: https://www.facebook.com/groups/785900308158525/
Liebe Frau Keller, haben Sie vielleicht eine Anregung? Ein Kollege arbeitet ökonomische Daten auf Länderebene auf und hat dementsprechend eine winzige Stichprobe (n=6), aber extrem viele hochspannende Variablen. Ihn interessieren in erster Linie Korrelationen. Ein wie kleines n verträgt der Spearman, bzw. gäbe es Alternativen, um sinnvoll zu arbeiten? Mir ist hier bei bestem Willen nichts bekannt. Besten Dank, Edith
Hallo Edith, es gibt keine Mindestanzahl. Dein Kollege kann also ruhig mit n=6 rechnen. Es ist allerdings so, dass man mit einer so kleinen Fallzahl nur sehr starke Zusammenhänge als signifikant nachweisen kann. Mit großen Fallzahl sind dagegen auch schon geringe Zusammenhänge als signifikant zu sehen. Es muss also bei der Interpretation immer alles mit berücksichtigt werden: Fallzahl, Korrelationskoeffizient und p-Wert.
Hallo Frau Keller,
Ich habe ein paar Fragen bezüglich möglichen Auswertungsverfahren.
1. Wie kann ich bei einer Eingruppen Prä-Post-Erhebung die Mittelwertdifferenz berechnen bzw. die Mittelwerte miteinander vergleichen (Zur Veränderungsmessung)? Mit dem Wilcoxon-Einstichprobentest?
2. Kann ich aus eigentlich ordinalen Skalen, die aber als intervallskaliert angenommen werden mit einer 5-stufigen Skala einen Mittelwert für die gesamte Stichprobe berechnen? Oder lediglich Mittelwerte pro Item angeben?
3. Wenn ich zwei quasi-intervallskalierte Skalen bezüglich ihres Zusammenhangs untersuchen möchte, welches Verfahren wende ich am besten an? Korrelation mit Spearman oder Kendalls-Tau?
Oder Kruskal-Wallis bei Nicht-Normalverteilung, ANOVA bei Normalverteilung?
Ich danke schon jetzt für Ihre Antwort.
Viele Grüße
Hallo,
zu 1: entweder die beiden Messungen mit einem Wilcoxon Test für gepaarte Stichproben auf Lageunterschied vergleichen oder die Differenzen „Post minus Prä“ mit dem Einstichprobentest von Wilcoxon zur 0 vergleichen.
zu 2: meinst du, du hast mehrere Items und möchtest die zu einer Skala zusammen fassen???
zu 3: Gehen beide: Spearman oder Kendall. Kruskla-Wallis und ANOVA sind für Gruppenunterschiede vonmehr als 2 Gruppen, passt hier also nicht.
Vielen Dank für die schnelle Antwort. 🙂
Zu 2.
Ich habe 6 5stufige Skalenitems und aus diesen einen additiven Index gebildet. Kann ich aus den Indizis/Summenwerten der einzelnen Versuchperson einen Mittelwert für die gesamte Stichprobe ziehen. Zum Beispiel ein Mittelwert von vielleicht 3,6 eines Indexes für die gesamte Stichprobe. Das würde mir den Vergleich der Prä-Post-Erhebung erleichtern… mittels t-Test bei Normalverteilung und Wilcoxon bei nicht normalverteilten Daten.
Wahrscheinlich ist diese Frage echt simpel, aber ich hab irgendwie ein Brett vorm Kopf! 😉
Danke schon jetzt!
Liebe Grüße
Den Summenwert kannst du wie eine „normale“ Variable verwenden, für diese Variable die dekriptiven Statistiken berechnen (Mittelwert usw.) und auch Tests drauf rechnen.
Hallo Daniela,
die Antworten haben mir sehr weitergeholfen.
Herzlichen Dank dafür!
Viele Grüße
Lexi
Hallo Daniela,
danke für die schnelle Antwort.
Liege ich richtig damit, dass es in meinem Versuch nur den Innersubjektfakor „Bedingung“ (mit 3 Stufen) gibt?
(Ich unterteile nach keinen weiteren Kriterien, wie Alter oder Geschlecht.)
Egal wie ich rechne, ich muss meine umstrukturierte Matrix benutzen, oder?
LG Lexi
Hallo Lexi, wenn die Bedingung die Messwiederholung ist, dann ist das der Innersubjektfaktor, ja. Wie sieht deine umstrukturierte Matrix aus? Mit den Messwiederholungen als Spalten? Dann: ja. Gruß Daniela
Hallo Frau Keller,
wenn ich eine einfaktorielle Varianzanalyse (1 Faktor, 3 Stufen = 3 unterschiedlichen Bedingungen) mit Messwiederholung und mehreren abhängigen Variablen habe, was ist dann der Innersubjektfaktor? Ich gehe davon aus, dass es die Bedingungen sind, bin mir aber nicht sicher.
Die Probanden verteilen sich gleichmäßig auf 3 Listen und die Items jeder Liste sind identisch, nur wird jedes Item über die 3 Listen verteilt in einer anderen Bedingung bearbeitet.
Jedes Item wird also von 3 verschiedenen Personen bearbeitet, wobei jede Person das unter einer anderen Bedingung macht. Die Messwiederholung kommt m. E. ins Spiel, weil jeder Proband unter jeder Bedingung arbeitet.
Meine Schwierigkeit ist, das in SPSS richtig einzugeben. Beispiele mit einer einzelnen abhängigen Variablen und mehreren Messzeitpunkten verstehe ich einzugeben, aber wie mache ich das unter den oben genannten Voraussetzungen?
Ich habe 5 abhängige Variablen.
Vor der Umstrukturierung hatte jede Person in der SPSS Matrix
3 Zeilen für sich, eine für Bed 1 und den Zeiten der 5 abhängigen Variablen, eine Zeile für Bed 2 …usw.
Nach Umstrukturierung meiner Daten habe ich folgendes Schema:
Pro Zeile eine Person und in den Spalten u.a. folgendes:
Zeit 1 Bed 1 ___Zeit 1 Bed 2___Zeit 1 Bed 3___Zeit 2 Bed 1___Zeit 2 Bed 2__ usw.
Ich brauche Hilfe bei der Bestimmung des Innersubjektfaktors. Normal gibt man einen Namen ein und die Anzahl der Stufen. Das wäre dann, falls ich richtig liege, Bedingung und 3
ODER
sind es die 5 abhängigen Variablen, die dann jeweils 3 Bedingungen haben, die ich eingeben muss?
Über eine Rückmeldung würde ich mich sehr freuen, da ich schier daran verzweifle.
Schönen Sonntag und danke schon einmal
Lexi
Hallo, bei mehreren abhängigen Variablen rechnest du entweder mehrere ANOVA-Modelle, oder eine MANOVA.
Der Innersubjektfaktor ist der Messwiederholungsfaktor, der Zwischensubjektfaktor ist der Gruppenfaktor.
Hallo Frau Keller,
ich habe folgende Fragen:
ich habe 35 verschiedene Variablen auf metrischem Skalenniveau erhoben (Verhaltensbeobachtung mittels Videoanalyse und entsprechendem Kodierschema, das 35 Variablen umfasst; Stichprobe>70). Ich möchte nun wissen, ob einzelne der Variablen signifikant voneinander abweichen. Kann ich dazu den Chi-Quadrat-Test verwenden, auch wenn metrische, nicht-normalverteilte Daten vorliegen? Wie interpretiere ich die Signifikanzwerte, wenn sie knapp an der „Signifikanzgrenze“ von p<0,05 liegen, z.B. p=0,053? Wie interpretiere ich die Signifikanz, wenn für Chi-Quadrat ein signifikantes p herauskommt, z.B. p=0,016, jedoch im Vergleich dazu der Monte-Carlo-Wert für die Signifikanz bei 0,07 liegt? Welcher Wert hat sozusagen mehr Bedeutung?
Ich würde mich sehr über Ihre Rückmeldung und Hilfe freuen! Danke.
Hallo, was genau möchtest du zeigen? Dass es signifikante Unterschiede in der Lage gibt (die Variablen haben unterschiedlich hohe Werte)? Dann wäre das ein Test auf Lageunterschied für verbundene Stichproben (z.B. ANOVA bei Normalverteilung, Kruskal-Wallis bei Nicht-Normalverteilung). Wenn du untersuchen willst, ob sich die Verteilungen der Variablen unterscheiden, dann wäre der Chi-Quadrat-Goodness of fit-Test für die Verteilungsanpassung zu wählen. Voraussetzungen an die Verteilung der Daten hat der nicht.
Ein knapper p-Wert bedeutet, dass du bei einer größeren Stichprobe wohl einen signifikanten Unterschied nachgewiesen hättest. Für deine Aussage mit diesen Daten bedeutet er: „Es kann kein signifikanter Unterschied nachgewiesen werden“. Es ist aber sinnvoll, den p-Wert zu nennen und zu diskutieren, dass er knapp an der Signifikanzgrenze liegt.
Der Wert der Monte-Carlo Simulation ist grundsätzlich verlässlicher, allerdings ist es interessant zu untersuchen, warum der so vom p-Wert des Chi-Quadrat-Tests abweicht. Hat der Chi-Quadrat-Test viele schwach besetzte Zellen (n<5)?
Hallo Daniela,
Im Zuge einer Zeitreihenanalyse für Verbrauchsmengen, möchte ich zunächst die Zeitreihe um Ausreißer glätten, bzw. Ausreißermenge auf z.B. den Median setzen. Die Frage ist allerdings, wie ich Ausreißer erkennen lasse?
Die Daten sind überwiegend nicht normalverteilt. Ich habe erst versucht eine zulässige Spannbreite von Median +/- 4 MAD aufzustellen und alternative artihmetischer Mittelwert +/- 2 Standardabweichungen, allerdings führt dies nicht immer zu korrekten Angaben, bzw. Kenntlichmachung von Ausreißerns… Muss ich folglich die Daten erst transformieren in normalverteilte Daten?
Die Lösung muss dabei in einer Excel-Funktion möglich sein, bzw. mit hilft keine grafische Lösung, da ich knapp 8.000 Datensätze à 25 Spalten prüfen lassen muss.
Vielen Dank für eine kurze Antwort
Gruß, René
Hallo René, wenn du eine passende Transformation findest (z.B. log), ist das sehr hilfreich, für die Identifikation von Ausreißern. Vor allem dann, wenn deine Daten im Moment schief sind (also in eine Richtung mehr streuen als in die andere).
Hallo Daniela
Ich habe eine unabhängige Variabel mit 3 Levels und mehrere abhängige Variablen. Ich möchte eine MANOVA in SPSS durchführen. Ich habe überprüft, mittels Saphiro-Wilks-Test, Historgammen, Q-Q-Plots usw. ob die Residuen normalverteilt sind oder nicht. Leider waren sie das nicht, bei etwa der Hälfte der Variablen. Ich habe nun für die einzelnen Variablen eine Transfomation gesucht (und gefunden), die dann zu einer Normalverteilung in den Residuen führt.
Meine Frage ist nun, ob es überhaupt zulässig ist, Variablen, die unterschiedlich transformiert wurden (ich habe Quadratwurzel und Reziprokwert verwendet), in die selbe MANOVA „reinzustecken“.
Würde mich sehr über eine Antwort freuen : )
Viele Grüsse
Dominik
Hallo Dominik,
ja, das ist zulässig.
Schöne Grüße
Daniela
Perfekt
Vielen Dank für die schnelle Antwort : )
Viele Grüsse
Dominik
Hallo Daniela,
ich muss eine MANOVA durchführen, um sagen zu können, ob eine Gruppenzugehörigkeit zu einem Modell (2 verschiedene Modelle) (also meine unabhängige Variable) Auswirkungen auf bestimmte andere Faktoren hat (etwa 10 abhängige Variablen). Im Prinzip soll dabei deutlich werden, ob die Probanden innerhalb des neueren Modells die Bedingungen anders wahrnehmen.
Nun ist mein Problem, dass die Stichproben dieser beiden Gruppen sehr unterschiedlich sind (etwa 180 Probanden in der ersten und 60 in der zweiten Gruppe).
Ich habe gelesen, dass die unterschiedlich große Stichprobe ein Problem sein kann, habe aber keine genauen Ausführungen finden können und frage mich jetzt, ob ich die Stichprobe irgendwie ändern muss und wenn ja, wie?
Außerdem habe ich gelesen, dass man vor einer MANOVA auch erst die Normalverteilung, Ausreißer, Varianzen und Korrelationen prüfen sollte. Die Aussagen sind jedoch sehr unterschiedlich, sodass ich nicht weiß, welche Faktoren ich in meinem Fall wirklich beachten muss. Können Sie mir da vielleicht einen Hinweis geben?
Ein großes Dankeschön im Voraus und viele Grüße
Katharina
Hallo Katharina,
die unterschiedlichen Stichprobengrößen sind kein Problem, wenn die Voraussetzungen (Normalverteilung, Homogenität usw) passen.
Die Voraussetzungen für die MANOVA sind zufälliges Sampling, unabhängige Residuen, multivariate Normalverteilung der Residuen, Homogenität der Varianz-Kovarianz-Matrizen.
Weitere Fragen gern in der Statistikfragen-Gruppe bei Facebook: https://www.facebook.com/groups/785900308158525/
LG
Daniela
Hallo Daniela,
ich möchte den Zusammenhang zweier ordinal skalierte Variablen (abhängig und unabhängig) testen und bin mir mittlerweile unsicher welcher Test der passende ist und vor allem was alles zu beachten ist.
– meine abhängige Variable ist ordinal (Klassen: 1-5 –> trifft gar nicht …. trifft voll zu)
– meine unabhängige Variable ist auch ordinal (1-5) (Haushaltsgröße – 1 Person .. 5 Personene und mehr)
– insgesamt wurden 1000 Personen befragt
Normalverteilung:
– Kolmogorow-Smirnowa: ist nicht signifikant (o.ooo)
– Q-Q-Plot: nur 5 Punkte (sind das die Klassen?) in der Grafik, die ganz leicht abweichen von der Geraden (in SPSS)
–> da ordinale Daten anscheinend nicht normalverteilt sein können, nehme ich an, dass das umsonst war?!
Nichtparametrische-Tests:
– bei Kruskal-Wallis und auch den anderen Test, wird oft mit einer Rangordnung gearbeitet. Da ich aber nur Werte von 1-5 habe entstehen sehr viele Ties?!
–> Ist der Test dann überhaupt sinnvoll?
– Tau-b: nur bei kleinen Stichproben?
Varianzhomogenität (Mittelwertvergleich)
– kann bzw. muss dieser gemacht werden vor K-W, Tau-b bzw. generell?
Wie du siehst, habe ich einige Fragen und bedanke mich schon im Voraus über eine Rückmeldung 🙂
Viele Grüße
Dominik
Hallo Dominik,
bei nur 5 Ausprägungen ist es schwierig, eine Normalverteilung nachzuweisen, also brauchst du nichtparametrische Methoden. Für die Korelation ist das Spearman oder Kendalls-Tau. Varianzhomogenität brauchst du hier nicht prüfen.
Allgemeine Fragen, die sich nicht auf den Blogbeitrag beziehen, kannst du gern weiter in der Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ stellen.
Schöne Grüße
Daniela
Hallo Frau Keller,
Ich habe einen Fragebogen mit Einmalmessung und ausschließlich nominalen Daten. Wie kann ich die Reliabilität berechnen? Ich habe kein SPSS, nur statistica in Studentenversion. Re-Test geht nicht, Split-half Methode bzw. interne Konsistenz bei nominalen Daten verstehe ich nicht. Können Sie mir helfen?
Liebe Grüße
Silvia Renner
Hallo Silvia,
wenn die Variablen dichotom sind, dann passt die Kuder-Richardson-Methode. Die wird in SPSS automatisch berechnet, wenn man Cronbachs Alpha berechnet und dichotome Variablen verwendet. Wie und ob es sie in Statistica gibt, weiß ich leider nicht.
Schöne Grüße
Daniela
Hallo Daniela,
ich stehe ziemlich auf dem Schlauch.
Im Zuge meiner Bachelorarbeit habe ich einige Hypothesen aufgestellt. Meine Daten sind nicht normalverteilt. Für die alters- bzw. geschlechtsspezifischen Hypothesen habe ich den Mann-Whitney-U-Test verwendet und bin mir jetzt durch Ihrer Aufstellung auch ziemlich sicher, dass das richtig war.
Mein Problem liegt in den Hypothesen, die die komplette Stichprobe betreffen. Ich möchte testen, ob sich in der Gesamtgruppe signifikante Tendenzen bei der Bewertung einzelner Statements erkennen lassen. Können Sie mir da weiterhelfen?
Vielen Dank und liebe Grüße
Martin
Hallo Martin, was genau meinst du mit „signifikante Tendenzen bei der Bewertung einzelner Statements“? Willst du die Statements vergleichen? LG Daniela
Hallo
ich habe eine 5-stufige Skale (Lehne völlig ab bis Stimme völlig zu) verwendet. Der Mittelpunkt (weder noch) wäre also die 3. Die MIttelwerte liegen natürlich nicht genau bei 3. Ich möchte für jedes der Statements testen ob die Abweichung signifikant ist.
Hallo Martin,
wenn du die Abweichung zum Mittelwert (also 3) untersuchst, dann passt da wohl der Wilcoxon-Einstichprobentest.
Schöne Grüße
Daniela
Hallo Daniela,
ich hab folgende Situation:
Ich untersuche Effekte bei der Blutlagerung von 10 Probanden. Das heißt, ich bereite das Blut zur Lagerung vor und nehme zum Zeitpunkt 0, 1,2,4 und 6 Wochen Proben um diese zu untersuchen. Ich habe keine Kontrollgruppe. Allerdings habe ich von den selben Probanden 3 Proben in wöchentlichen Abstand aus dem Körper entnommen, um sozusagen die „normalen“ Werte zu bekommen.
1. Wie untersuche ich am besten, ob es signifikante Unterschiede zwischen Körper und Blutbeutel gibt?
2. Wie stelle ich fest ob, es zwischen den 3 Proben aus dem Körper signifikante Schwankungen gibt? Das selbe möchte ich natürlich aus dem Blutbeutel wissen.
Vorab schon mal vielen Dank für deine Hilfe.
glg Kitty
Hallo Kitty,
das werden wohl, je nach Messniveau und Verteilung, Kreuztabellen, Varianzanalysen oder Kruskal-Wallis-Tests werden. Lade dir doch mein kostenloses E-Book herunter. Da findest du eine Anleitung, wie du die richtige Methode auswählst.
LG
Daniela
Hallo Daniela,
ich muss eine ANOVA durchführen, um festzustellen, dass es zwischen dem wahrgenommenen risiko und der kundenzufriedenheit ein zusammenhang besteht. wie mache ich das am besten? die antworten habe ich in form von likert-skala antworten. Die beiden Variablen sind dann intervall (ordinal) skaliert, wie ich verstehe. Die UV muss aber nominal skaliert sein. Ich verstehe auch nicht ganz, wie ich dann die Gruppen bilden soll….In den Beispielen, die ich gefunden habe, sind die Gruppen zbsp. Altersgruppen o.ä. Aber wenn ich die Gruppen nach dem Alter bilde, wird es nicht bedeuten, dass ich den Zusammenhang zw. dem Alter und der Kundenzufriedenheit beweise?
Vielen-vielen Dank!
Viele Grüße
Nadja
Hallo Nadja,
du kannst entweder einen Zusammenhang zwischen den beiden Likert-Variablen durch eine Korrelation berechnen, oder du nimmst eine Likert-Variable als Gruppierung (eventuell zu weniger Gruppen zusammen gefasst, damit es nicht so viele Gruppen sind, ob ordinal oder nominal ist als Gruppierungsvariable egal) und untersuchst die andere Variable dazwischen auf Lageunterschiede. Für die ANOVA sollten die Daten aber normalverteilt sein, das müsstest du vorab checken.
Schöne Grüße
Daniela
Hallo Daniela!
Vielen, vielen Dank für die Antwort!! Habs verstanden und werde mal schauen welche Alternative ich nehme 🙂
Viele Grüße
David
Hallo Frau Keller!
Vielen Dank für die Erklärung oben! Ich habe bei meiner Bachelorarbeit die Situation, dass ich eine Variable (keine Normalverteilung) habe, dessen Werte sich zu 70% auf einen niedrigen Wert beziehen und die restlichen 30% sich jeweils minimal auf die höheren Werte aufteilen…ist es bei solch einer Verteilung noch „seriös“ eine Korrelation zu rechnen?
Mit freundlichen Grüßen und vielen Dank!
David Werner
Hallo David,
was meinen Sie mit „auf niedrigen Wert beziehen“? Haben 70 % der Werte diesen niedrigen Wert?
Schöne Grüße
Daniela Keller
Hallo Daniela,
ja genau, 70% der Werte haben diesen niedrigen Wert. Im Diagramm hat es vom Verlauf her Ähnlichkeiten zu der Funktion log 1/2 x.
Viele Grüße
David
Haben 70 % der Werte GENAU diesen Wert? Also z.B. 70 % haben den Wert 0,1 und 30 % der Werte haben genau den Wert 5,0?
Hallo Daniela,
also es handelt sich um die Menge an konsumiertem Alkohol in Gramm in einem bestimmten Zeitraum. 70% haben genau 0 Gramm angegeben und die restlichen 30% haben sich auf verschiedene Werte zwischen 1 bis hin zu 20 Gramm aufgeteilt. Das aber halt relativ gleichmäßig.
Ist ein bisschen schwer zu erklären 😉
VIele Grüße
David
Hallo David,
alles klar, jetzt hab ichs 😉
Mit 70 % ist das ein sehr hoher Anteil an Bindungen (=gleiche Ausprägungen). Für die Spearman-Rangkorrelation ist das zu viel (maximal 20 % wird da empfohlen). Stattdessen wird hier der Koeffizient Kendall-Tau-B empfohlen. Der soll bei vielen Bindungen und/oder kleinen Stichproben immernoch zuverlässig sein. Ich persönlich finde aber 70 % trotzdem noch sehr hoch, wäre also mit den Ergebnissen trotzdem kritisch. Eventuell macht es Sinn, die Variable zu gruppieren: 0, 1-10, 10-20, und dann damit weiter zu untersuchen (z.B. Test auf Lageunterschiede zwischen den Gruppen…)
Schöne Grüße
Daniela
Guten Tag Frau Keller,
ich habe ein Problem mit meinen statistischen Auswertungen. Ich möchte eine ANCOVA durchführen, jedoch werden die Voraussetzungen nicht erfüllt. Gibt es hierzu ein nicht parametrisches Alternativverfahren? Da dich Stichproben starke Unterschiede bzgl. der Größe aufweisen (von 2 bis 51 VP pro Gruppe) kann ich mich auch nicht darauf beziehen, dass die ANCOVA relativ robust gegen Verletzungen der Voraussetzungen ist.
Viele Grüße Heike B.
Hallo Heike,
nein, zur ANCOVA gibt es keine nichtparametrische Alternative. Versuchen Sie, Ihr Modell zu vereinfachen: Reichen z.B. auch mehrere Paarvergleiche oder die Verwendung der Kovariaten als Gruppierung … Die extrem kleine Gruppe mit 2 Versuchspersonen ist aber wohl für jede Methode ein Problem. Vielleicht können Sie die aus der Analyse weglassen und damit nur deskriptiv arbeiten? Oder Sie fassen Sie sinnvoll mit einer anderen Gruppe zusammen?
Ich hoffe, die Anregungen helfen etwas weiter!
Schöne Grüße
Daniela Keller
Danke für ihre schnelle Antwort und ihre hilfreichen Anregungen.
Viele Grüße Heike
Hallo, ich habe 2 Fragen:
1. Ich habe den Shapiro-Wilk Test angewendet, um auf eine Normalverteilung zu testen. Dann bekomme ich ein p-Wert heraus, den ich aber nicht recht einzuschätzen weiß. Ich habe häufig gelesen, dass der p-Wert nur ausreichend groß sein muss, damit eine Normalverteilung vorliegt, jedoch ist „ausreichend groß“ sehr schwammig und reine Auslegungssache und daher bisher kaum zitier-fähig. Gibt es dazu vielleicht eine bessere Aussage, oder noch besser ein Buch, welches man zitieren kann?
2. Dieses Problem betrifft die gleiche Studie und ist daher auch dem Bereich „Anwendung“ zuzuordnen: Der Datensatz ist nicht normalverteilt und daher wollte ich den Wilcoxon-Test anwenden. Jedoch sind die Datensätze (>2) zudem nicht stetig, d.h. es bliebe nur der Chi-Quadrat-Test übrig. Dieser ist aber, wenn ich das richtig verstanden habe, zu ungenau, da er nur angibt, ob ein signifikanter Unterschied vorliegt, aber keine Aussage über die Rangfolge macht. – Eigentliche Frage: Ist es in der Anwendung nicht auch erlaubt, die „nicht-Stetigkeit“ zu ignorieren? Gibt es da vielleicht Quellen (Dissertationen, Bücher)?
Viele Grüße,
Julian
Hallo Julian,
zu 1: Bei einem p-Wert von kleiner 0,05 lehnt der Shapiro-Wilk Test die Normalverteilung ab.
zu 2: Der Wilcoxon Test (genauso wie auch die anderen nichtparametrischen Tests) arbeitet mit Rängen, deshalb kann ihn auch auf ordinalen Daten mit vielen Ausprägungen verwenden. Die Daten müssen also nicht stetig sein. Wenn mehr als 2 unverbundene Gruppen verglichen werden sollen, ist das der Kruskal-Wallis Test. Wenn mehr als 2 verbundene Stichproben verglichen werden sollen, ist es der Friedman. Auch diese Tests für den Vergleich von mehr als 2 Stichproben sagen nur, ob es irgendwo einen signifikanten Unterschied gibt. Um herauszufinden, wo der ist, müssen immer Paarvergleiche gemacht werden (das wäre dann wieder Wilcoxon oder Mann-Whitney U).
Schöne Grüße
Daniela Keller
Hallo,
1. ich möchte Mittelwerte aus drei verschiedenen Gruppen(30km/h; 40 km/h und 50 km/h) miteinander auf Signifikanz untersuchen!!! Die Werte sind laut SPSS normal verteilt. Welcher Test ist am Besten dafür geeignet?
2. Wie genau mache ich ein Chi Test auf Unabhängigkeit mit SPSS?
Vielen Lieben Dank im Voraus!
Hallo,
1. ANOVA
2. Analysieren -> Deskriptive -> Kreuztabellen, Statistik: Chi-Quadrat
Schöne Grüße
Daniela Keller
Hallo Frau Keller,
toll das Sie so auf Fragen eingehen! da hätte ich auch eine 😉 Es geht um das Thema der Ausreißerbereinigung.
Ich habe eine Studie mit drei Aufgaben, also drei Messwiederholungen pro Proband. Um Reihenfolgeeffekte auszubalancieren, habe ich ein lateinisches Quadrat genutzt und dementsprechend drei Experimentalgruppen mit je drei Aufgaben. Hierdurch will ich mit den Gesamtmittelwerten der jeweiligen Aufgabe weiterrechen. Abhängige Variable ist dabei eine Reaktionszeit in Millisekunden.
Ich frage mich nun zum einen, mit welcher Methode/Herangehensweise ich Ausreißer bereinige, ob ich einen kompletten Datensatz eines Teilnehmer bei einer der drei Aufgaben eliminieren muss oder nur seine Extremwerte in einer der Aufgaben. Weiterhin, ob ich zur Identifikation der von Extremwerten dann als Bezugsgröße den Mittelwert der Aufgabe (mit allen drei Gruppen) oder nur den Mittelwert seiner eigenen Gruppe nutzen muss.
Sie wären mir eine große Hilfe wenn Sie mir eine Idee geben könnten oder gern auch eine Literaturempfehlung (habe zu meiner Speziellen Frage leider nichts gefunden)
Vielen Herzlichen Dank
Stephan
Hallo Stephan,
wieso wollen Sie denn Ausreißer bereinigen? Ausreißer sollte man nur bereinigen, wenn man einen guten Grund dafür findet (unrealistischer Wert; Tippfehler; besonderer Teilnhemer, der nicht zur Zielgruppe passt, usw.). Ansonsten sollten Sie alle Werte drin lassen. Für die Analyse brauchen Sie dann eventuell eine Methode, die nicht anfällig auf Ausreißer reagiert, also z.B. den Median als Lagemaß statt Mittelwert verwenden und für Tests nichtparametrische Methoden einsetzen.
Schöne Grüße
Daniela Keller
Hallo Daniela,
danke für Ihre schnelle Antwort und entschuldigen Sie meine verzögerte.
Da ich die Reaktionszeiten der Versuchspersonen auch über eine Online-Erhebung gemessen habe, geben ein paar Daten den überzeugenden Hinweis, dass ein paar davon nebenher noch etwas anderes gemacht haben. Kurz gesagt: Extrem unrealistische Reaktionszeiten. Ich habe mich jetzt an die klassische Identifikation über Box-Plots gehalten und die kompletten Fälle entfernt.
Im Zusammenhang mit solchen Reaktionszeitmessungen gibt es wohl auch Konfundierungen mit Latenzzeiten. Irgendwo habe ich dazu gelesen, dass man in solchen Fällen auch einen oberen cut-off-Wert bestimmen kann (z.B. 1,5 SD) und die Daten anschließend für eine Varianzanalyse logarithmiert.
Ich hoffe ich überspanne den Bogen des Fragens nicht aber eine Frage hätte ich noch 😉
Meine 3 (leicht vs. mittel vs. schwer)x2 (Linkshänder vs. Rechtshänder) x2 (Online- vs. Laborerhebung) ANOVA mit Messwiederholung auf dem ersten Faktor und 2 AV´s (Reaktionszeit und Zufriedenheit), ergab einen signifikanten (within) Haupteffekt auf beide AV´s. Interaktionseffekte (between) wurde nicht signifikant. Die Diagramme geben jedoch den grafischen Hinweis, dass sich auf der dritten Stufe der ersten UV (schwere Aufgabe), die AV Zufriedenheit hinsichtlich der Ausprägung der UV Händigkeit unterscheidet (Linkshänder zufriedener). Ist es legitim da einen einzelnen t-Test durchzuführen?
Ich habe mir auch die Konfidenzintervalle für die 6 Mittelwerte (ohne Online vs. Labor) angeschaut und festgestellt, dass die sich alle überschneiden. Jetzt wundere ich mich auch etwas, da sich die KI´s der Links- und Rechtshänder bei jeder Aufgabenschwierigkeit untereinander und zwischen einander überschneiden – obwohl laut der ANOVA ein Haupteffekt der Aufgabenschwierigkeit besteht.
Vielen Dank zur späten Stunde und wenn der Bogen überspannt sein sollte gibt er wenigsten einen schönen Ton bei Zupfen von sich 😉
Beste Grüße
Stephan
Hallo Stephan,
zu den Reaktionsszeiten: eine Identifizierung über Boxplots ist sinnvoll. Die Transformation mit dem Logarithmus macht dann Sinn, wenn die Daten nach der Transformation annähernd normalverteilt sind: Ausprobieren!
Eine Untersuchung von speziellen Unterschieden mit Paarvergleichstest können Sie machen. Wenn Sie auf der gleichen Hypothese testen, müssen Sie beachten, dann das Signifikanzniveau anzupassen.
Vielleicht ergibt sich der Effekt der Aufgabenschwierigkeit im extremsten Unterschied zwischen leicht und schwer und diese beiden überlappen sich nicht? Oder der Haupteffekt wird durch Kontrolle der anderen Faktoren erst deutlich, was eventuell in den Konfidenzintervallen nicht klar wird, wenn Sie nicht nach jedem Faktor gruppieren?
Schöne Grüße
Daniela Keller
Hallo Frau Keller,
es lag ein Fehler meinerseits vor, da ich wohl die SPSS-Outputs nicht ganz korrekt gelesen habe. Bei dem Haupteffekt hat SPSS gleich einen nach Bonferroni angepassten Paarvergleich durchgeführt (anhand der Mittelwertsdifferenzen). Die Konfidenzintervalle der Interaktionen wurden nicht einer Alpha-Justierung unterzogen – vermutlich weil die Interaktionen nicht signifikant geworden sind. Sie überschneiden sich eh in jeder Stufe der Aufgabenschwierigkeit.
Was mich noch etwas verunsichert ist, dass eine der Zufriedenheitsmessungen (AV) im Levene-Test signifikant geworden ist. Als einzige AV – die anderen zwei Zufriedenheitsmessungen sehen gut aus und die Logarithmierung der Reaktionszeit hat hier gutes Bewirkt! Da jedoch die wichtigere Voraussetzung der Sphärizität gegeben ist, gehe ich davon aus, dass dieses einzelne Ergebnis im Levene-Test nicht ins Gewicht fällt.
Soweit so schön. Nun wapne ich mich für den Kampf eine regressionsanalytische Vorhersage zu bewerkstelligen, bei welcher Reaktionszeit innerhalb einer bestimmten Aufgabenschwierigkeit eine bestimmte Zufriedenheitsausprägung entsteht. Die grundlegende Frage dabei ist z.B. ab welcher Reaktionszeit bei schweren Aufgaben eine Zufriedenheit von 7 oder höher auf einer neunstufigen Skala erreicht wird.
Falls Sie mir hierfür einen kleinen grundsätzlichen Tip hätten… Ist mir ja schon fast unangenehm Sie zu löchern!
Herzliche Grüße
Stephan
Hallo Stephan,
wenn Sie bei Zufriedenheit an hoch/niedrig interessiert sind (>=7/<7), dann wäre das als Regressionsmodell eine logistische Regression. Sie untersuchen dann, wie die Reaktionszeit auf Zufriedenheit hoch/niedrig wirkt. Allerdings bekommen Sie da nicht heraus, ab welcher Reaktionszeit die hohe zufriedenheit erreicht wird. Das hört sich für mich eher nach einer ROC-Analyse an (ROC-Kurve, AUC). Die wird normalerweise für diagnostische Tests verwendet, um zu sehen, ab welcher Höhe des Laborparameters der Patient als Krank eingestuft werden soll. Bei Ihnen wäre das dann: Wo muss ich bei Reaktionszeit den Cutoff setzen, damit ich Zufriedenheit hoch/niedrig gut voraussagen kann.
Vielleicht wär das ja was...
Schöne Grüße
Daniela Keller
Liebe Daniela,
ich habe auch eine Frage. Ich habe zwei, unabhängige Stichproben (eine normalverteilt, eine nicht normalverteilt) auf einen signifikanten Unterschied bezüglich eines Parameters verglichen. Ich verwendete den Mann-Whitney-U-Test. Ich habe einen signifikanten Unterschied und eben die mittleren Ränge erhalten. Hat die Gruppe mit dem höheren mittleren Rang dann auch durchschnittlich höhere Werte bzgl. des Parameters?
Dann tat sich ein weiteres Problem auf. Der Parameter, den ich untersucht habe berechnet sich aus einen Quotienten (Bsp.: x=a/b). Jetzt kann x klein sein wenn a klein ist und b groß oder aber wenn a und b beide groß sind usw. Ich möchte also erklären wie es zu dem hohen/niedrigern Wert der mittleren Ränge kam, also ob a groß war und b klein usw. Reicht in diesem Fall der Median aus (eine Stichprobe nicht normalverteilt)? Kann/sollte ich in der normalverteilten Stichprobe den Mittelwert heranziehen oder Median und den Mittelwert? Oder verwendet man in diesem Fall ein spezielles Testverfahren?
Ich hoffe ich konnte meine Frage einigermaßen verständlich erklären 🙂
Lieben Dank Dir schon einmal! Ich find das ganz super, dass du deine Hilfe anbietest!
Liebe Grüße
Stephanie
Liebe Stephanie,
ja, die mittleren Ränge werden genauso wie die Mittelwerte interpretiert: größerer mittlerer Rang = größere Werte im Mittel.
Zu Mittelwert oder Median: bei nicht normalverteilten und nicht symmetrisch verteilten Variablen ist der Median besser. Bei normalverteilten Variablen sollte der Median ziemlich genau dem Mittelwert entsprechen. Wenn man beides angibt, macht man nichts falsch. Wenn man nicht beides angeben möchte oder nicht genug Platz hat, sollte man sich überlegen, was für den Leser und/oder Prüfer besser ist. Wer noch nie etwas vom Median gehört hat, kommt mit dem Mittelwert besser klar. Wenn Boxplots als Abbildungen verwendet werden, ist der Median wieder besser, da man in den Abbildungen den dann sieht. Also, eine klare Antwort kann ich nicht geben. Es kommt darauf an … 🙂
Schöne Grüße
Daniela Keller
Ganz lieben Dank! Das hilft mir auf jeden Fall weiter!
Hallo Daniela,
leider reagiert die Statistikberatung meiner Hochschule seit Tagen nicht. Daher meine beiden Fragen nun an dich.
1) Ist es korrekt, dass man bei Vorliegen zweier unabhängiger Stichproben mit ordinalen Merkmalen gleich den U-Test anwenden kann, ohne erst noch auf Normalverteilung prüfen zu müssen und trotz dessen, dass beide Stichproben >10 sind?
2) Wäre unter Umständen bei Normalverteilung in beiden Stichproben trotz ordinaler Merkmale dennoch ein unabhängiger T-Test möglich? Falls ja, für welchen Test sollte ich mich bestenfalls entscheiden?
Vielen herzlichen Dank für deine Hilfe!
Felix
Hallo Felix,
streng genommen, darf bei ordinalen Variablen kein parametrischer Test verwendet werden. Aber die Definition einer ordinalen Variable ist auch nicht immer ganz klar, deshalb kann man trotzdem mal nach der Verteilung schauen und den t-Test verwenden, wenn sie normalverteilt sind. Andererseits macht man mit dem Einsatz von nicht-parametrischen Methoden auch nichts falsch. Die dürfen auch verwendet werden, wenn Normalverteilung vorliegt.
Schöne Grüße
Daniela Keller
Hallo Daniela!
Ich bin wahnsinnig froh, wenn auch zu später Stunde, auf diese Seite gestoßen zu sein….nicht nur, dass man sieht, das es noch viele andere Verzweifelte gibt, bringst du tatsächlich Licht ins Dunkel der Statistik:)
Ich wollte dich gerne fragen, wie du meine Daten berechnet und anschließend graphisch dargestellt hättest…jeder Statistiker nennt mir leider etwas anderes…
Ich habe zwei Gruppen bezüglich mehrerer Laborparameter zu vier Zeitpunkten miteinander verglichen. Pro Gruppe habe ich 20 Personen eingeschlossen (insgesamt also 40), sodass mir gesagt wurde, dass die Daten aufgrund der kleinen Gruppengröße nicht normalverteilt seien.
1.) Stimmt das so bzw. womit ikann ch überprüfen, ob eine Normalverteilung/nicht-Normalverteilung vorliegt?
2.) Falls die Daten nicht-normalverteilt sein sollten, hälst du eine Rangvarianzanalyse nach Brunner mit Messwiederholunge für sinnvoll, um die Signifikanz für den Gruppenunterschied über den Zeitverlauf zu berechnen?
(Habe ich richtig verstanden, dass man mit dieser Methode a) den Gruppenunterschied (A vs B) bezüglich der Mittelwerte zu einem bestimmten Zeitpunkt b) den Unterschied der Mittelwerte innerhalb einer Gruppe zu verschiedenen Zeitpunkten und c) den Gruppenunterschied über den Zeitverlauf bestimmt?)
3.) Würdest du die Daten mittels Box-and-whiskers-plot graphisch darstellen wenngleich die Rangvarianzanalyse Mittelwerte vergleicht? Und falls ja, dann einfach die Ergebnisse/Signifikanz unterhalb dem Graphen im Fließtext beschreiben? (Bzw. an welcher Stelle im Graphen markiere ich noch zusätzlich ein p < 0,005 bspw mittels *)?
Wie du merkst, herrscht ein ziemliches Durcheinander und ich hoffe, Du kannst mit weiterhelfen….
Tausend Dank im Voraus!
p<0,05 meinte ich…
Liebe Anna,
ich freue mich, dass Ihnen meine Seite gefällt und nützt! Zu Ihren Fragen:
1) Dass die Fallzahl 20 ist sagt nicht, dass sie nicht normalverteilt sind. Sie können die Normalverteilung über Quanitlplots oder Tests auf Normalverteilung (z.B. Shapiro-Wilk oder Kolmogorov-Smirnoff, aber Achtung, die sind zu streng!) überprüfen. Bei Laborparametern lohnt sich auch manchmal eine Transformation der Daten mit dem Logarithmus, der die Werte dann normalverteilt macht.
2) Die Rangvarianzanalyse nach Brunner kann (soweit ich weiß) nur 2 Gruppen und 2 Zeitpunkte untersuchen. Sie haben ja 4 Zeitpunkte. Ich würde die Daten erstmal mit Boxplots darstellen. Und dann überlegen, ob sich die Beschränkung auf zwei Zeitpunkte anbietet, z.B. erster und letzter. Dann könnten Sie die genannte Methode verwenden. Oder Sie berechnen dann einfach die Differenzen dieser Messzeitpunkte für jeden Patienten und vergleichen diese Differenzen zwischen den beiden Gruppen z.B. mit einem Mann-Whitney U Test. Dann sehen Sie, ob sich die beiden Gruppen über die Zeit signifikant unterschiedlich geändert haben. Das wäre dann Ihr Punkt c). Die anderen Punkte a) und b) können Sie mit einem Mann-Whitney U Test für jeden Zeitpunkt (a) und einer Friedman-ANOVA für jede Gruppe (b) untersuchen.
3) Der Boxplot ist hier eine gute Darstellungsmöglichkeit. Die Rangvergleiche untersuchen auch nicht die Mittelwerte, sondern die mittleren Ränge.
Schöne Grüße
Daniela Keller
Hi Daniela,
Coole Seite. Ich habe auch eine Frage. Vielleicht haben sich das auch schon andere gefragt.
Wenn ich nun schauen will, ob sich Gruppen (zB Altersklassen) im Hinblick auf eine AV unterscheiden und einen H-Test anwnde. Dann kann ich ja erkennen, ob global ein sig Unterschied vorliegt und falls ja mit Post-Hoc wo der oder die Unterschiede liegen.
Kann es nun auch Sinn machen zusätzlich eine Spearman Korrelation zu rechnen, um zu prüfen ob ggf sogar ein monotoner Zusammenhang vorliegt? Oder schließt sich das eigentlich aus? Sollte man sich lieber auf eines beschränken?
Viele Grüße
Janne
Hallo Janne,
ja, die Korrelation können Sie zusätzlich machen, um zu sehen, ob der Zusammenhang monoton ist. Das passt dazu, ist eine erweiterung der bisherigen Fragestellung (Lageunterschied).
Schöne Grüße
Daniela Keller
Hallo Daniela,
vielen Dank für deine hilfreichen Antworten. Du hast mir sehr geholfen.
Du schaffst es in wenigen Sätzen das zu erklären, was die Professoren bei uns in einem Semester nicht hinbekommen. Vielen lieben Dank dafür.
Liebe Grüße
Sabina
Danke! 🙂
Hallo Daniela,
vielen herzlichen Dank für diese tolle Übersicht. Ich beschäftige mich mit einem Problem, welches glaube ich in einem früheren Kommentar bereits angesprochen wurde.
Ich habe von 4 Probandengruppen jeweils 17 Laborparameter, welche vor, während und nach einer Intervention erhoben worden sind. Diese sind nun zu vergleichen, die Graphiken dazu sehen auch ganz schön aus, aber wie teste ich das jetzt auf Signifikanz? Muss ich an jedem einzelnen Untersuchungspunkt den Mittelwert der Gruppe einzeln prüfen (in dem Fall Mann-Whitney da nicht normalverteilt)? In welchem Fall macht es Sinn sich die Area under the curve zu betrachten und zu vergleichen? (dann auch wieder mit Mann-Whitney?)
Vielen herzlichen Dank,
Sabine
Hallo Sabine,
welche Methode Sie hier verwenden, hängt davon ab, was genau Sie untersuchen möchten bzw. was Ihre Fragestellung ist. Möchten Sie Unterschiede zwischen den Probandengruppen herausfinden? Oder möchten Sie Unterschied vor und nach der Intervention für jede Probandengruppe einzeln untersuchen? Oder möchten Sie die Änderung vor-nach zwischen den Probandengruppen vergleichen? Geht es bei den Probandengruppen immer um Paarvergleiche, oder interessiert, ob es irgendwo zwischen den Gruppen Unterschied gibt? …
Sie sehen, da ist viel möglich und eventuell brauchen Sie davon auch fast alles. Am besten, Sie schreiben sich jede Fragestellung so präzise wie möglich auf, überlegen sich dann: Sind das verbundene Messwerte (Messwiederholung vorher/nachher) oder unverbundene Stichproben (Probandengruppe 1, 2, 3, 4)? Sind es zwei oder mehr, die verglichen werden sollen? Anhand dieser Liste können Sie dann für jede Fragestellung die richtige Methode auswählen.
Noch ein Tipp: Bei Laborparametern, die sich nicht als normalverteilt erweisen, nützt es oft, eine Logtransformation durchzuführen, die dann die Werte normalverteilt macht. Das nur am Rande 🙂
Schöne Grüße
Daniela Keller
Noch ein Nachtrag: Die Area Under the Curve (AUC) macht immer dann Sinn, wenn Sie einen Goldstandard, z.B. für eine Diagnose haben. Also z.B. krank ja/nein, und möchten wissen, ob der Laborparameter ein guter Prädiktor dafür ist. Für AUCs können Konfidenzintervalle berechneet werden. Der Vergleich der Konfidenzintervalle für verschiedene Parameter ermöglicht dann Aussagen dafürber, welcher Parameter besser ist und ob der Unterschied deutlich/signifikant ist.
Hallo Daniela,
vielen Dank für die rasche Antwort. Wir hatten 4 Probandengruppen, welchen jeweils Prä- peri- und postinterventionell Blut entnommen wurde. Der Verlauf der Laborparameter der einzelnen Gruppen ist nicht entscheidend, es geht um den unterschiedlichen Kurvenverlauf zwischen den einzelnen Gruppen (steigt bzw. fällt ein Wert signifikant höher bei Gruppe 1 im Vergleich zu 2 usw.,)
Beste Grüße
Sabine
Hallo Sabine,
da macht es dann entweder Sinn, sich die Differenzen anzusehen: Also, erst Differenzwerte ausrechnen (Peri minis Prä und/oder Post minus Prä und/oder Post minus Peri). Und diese neu berechneten Werte dann zwischen den 4 Gruppen zu vergleichen (bei nicht Normalverteilung: alle 4 Gruppen: Kruskal-Wallis Test, jeweils 2 Gruppen: Mann-Whitney U Test).
Auch schön wäre eine mehrfaktorielle ANOVA mit Messwiederholung auf den Originaldaten (nicht auf den Differenzen): Faktor Messwiederholung und Faktor Gruppe. Die geht aber nur, wenn die Daten annähernd normalverteilt sind. Eventuell durch Transformation?
Schöne Grüße
Daniela Keller
Hallo Daniela,
vielen herzlichen Dank für deine Antwort.
Sie hilft mir sehr weiter, denn meine Verteilung ist mir jetzt bekannt. Ich habe KEINE Normalverteilung. Dann kann ich den Fisher-Test für meine Variablen verwenden, die jeweils zwei Kategorien haben. Jedoch habe ich auch Variablen mit drei Kategorien. Wähle ich dann den Chi-Quadrat-Test? Den Chi-Quadrat Test darf ich auch nehmen, wenn ich dichotome Variablen habe, richtig?
Mir ist der Unterschied zwischen dem Fisher und Chi-Quadrat Test nicht ganz klar. Der Chi-Quadrat Test ist ein nichtparametrischer Test und kann sowohl für Variablen mit zwei oder drei Kategorien verwendet werden. Bei dem Fisher Test muss die Verteilung bekannt sein und er ist nur für dichotome Variablen geeignet?
Vielen Dank im Voraus.
Veste Grüße
Sabina
Hallo Sabina,
kategoriale Variablen (dichotom oder mehrere Kategorien) werden gar nicht auf Normalverteilung überprüft. Du hast da natürlich keine Normalverteilung.
Ja, wenn Du zwei dichotome auf Zusammenhang überprüfst, dann nimmst Du Fisher. Bei mehr als zwei Kategorien geht der Fisher nicht, deshalb nimmst Du hier den Chi-Quadrat-Test, das stimmt. Der Chi-Quadra-Test ist auch bei 2×2-Tabellen möglich, ist aber nicht so genau wie der Fisher, deswegen nimmt man da lieber den Fisher.
Die Verteilung muss nie bekannt sein. Aber die Statistiksoftware berechnet sich aus den Häufigkeiten intern eine Statistik (das ist eine Zahl, die nach einer bestimmten Formel berechnet wird). Und beim Fisher-Test ist bekannt, wie diese Statistik exakt verteilt ist. Beim Chi-Quadrat-Test wird die Verteilung der Statistik nur approximiert, also angenähert, und ist deshalb nicht so exakt. Das passiert aber alles intern, darüber musst Du nichts wissen.
Die Regel ist einfach so: Bei 2×2-Tabellen verwendest Du Fisher, bei größeren Tabellen verwendest Du Chi-Quadrat.
Schöne Grüße
Daniela Keller
Hallo!
Bei 2 unabhängigen Stichproben mit nicht parametrischer Verteilung wird ja dementsprechend ein Mann-Whitney-U-Test angewandt… aber was macht man, wenn es nur metrische Daten sind (ich muss die Daten zweier Methoden vergleichen, d.h. ob mit den Methoden ähnliche Werte raus kommen)? Wird der Mann-Whitney-U-Test nicht bei einer ordinalskalierten Variable verwendet? Gibt es alternative nicht parametrische Tests für nur metrische Daten?
Bin gerade etwas ratlos und würde mich über einen Tipp freuen!
Herzliche Grüße,
Linda
Liebe Linda,
wenn Sie zwei metrische Variablen haben, die Sie auf Lageunterschied untersuchen möchten, und die Daten nicht normalverteilt sind, dann nehmen Sie den Mann-Whitney U Test. Dem ist es egal, ob es metrische oder ordinale Variablen sind. Man könnte ihn sogar bei Normalverteilung verwenden.
Schöne Grüße
Daniela Keller
Hallo Daniela,
ich habe eine Frage zu einem statistischen Test. Wo wird der exakte Fisher Test eingeordnet? Zählt er zu den parametrischen oder zu den nichtparametrischen Tests?
Vielen Dank.
Herzliche Grüße
Sabina
Hallo Sabina,
hm, die Daten für den exakten Fisher Test müssen dichotom sein. Es ist also kein Thema, wie sie verteilt sind. Anders als dichotom ist der Test überhaupt nicht sinnvoll. Deshalb würde ich ihn weder zu den parametrischen noch zu den nichtparametrischen Tests zählen. Allerdings ist es ein exakter Test, es wird also keine angenäherte Verteilung der Teststatistik verwendet, sondern die Verteilung der Teststatistik ist exakt bekannt. Deshalb ist der p-Wert auch exakt. (Das ist allerdings nicht die Antwort auf Deine Frage…) Hilft Dir das weiter?!?
Schöne Grüße
Daniela
Hallo Daniela,
super Artikel!
Aber etwas habe ich noch nicht so richtig verstanden. Ist es denn möglich, dass ich in meiner Arbeit in Tabellen oder Diagrammen arithmetische Mittelwerte darstelle und trotzdem einen H-Test oder U-Test rechne, um auf sig. Gruppenunterschiede zu prüfen?
Also z.B. Pflegetage nach Altersklassen, Pflegetage nach Geschlecht, Pflegetage nach sozialer Schicht usw.? Also klar gibts da auch bestimmt gewisse Zusammenhänge, aber die interessieren mich nicht. Ich will bloß eine einfache Aufschlüsselung; keine „Erklärung“ der Pflegetage oderso.
Ganz liebe Grüße
Bea
Hallo Bea,
ja, das ist möglich. Wenn die Daten sehr schief sind oder es Ausreißer gibt, ist zwar der Median passender als Lagemaß, aber den Mittelwert kannst Du natürlich auch ausrechnen und angeben. Oft wird er bevorzugt, weil er geläufiger ist als der Median…
Schöne Grüße
Daniela
Super danke!
Das heißt es ist nicht merkwürdig das „Eine“ darzustellen und das „Andere“ (also den Median) als Berechnungsgrundlage zu nutzen?
Ganz liebe Grüße
Bea
Naja, perfekt passt es nicht. Aber es wird oft gemacht. Außerdem verwenden die Tests ja auch nicht wirklich den Median, sondern die Ränge. Streng genommen würde dazu also der mittlere Rang passen (der z.B. von SPSS auch dazu ausgegeben wird). Aber der wird so gut wie nie verwendet.
Schöne Grüße
Daniela
Hallo Frau Keller,
mir schwirren so viele Daten durch den Kopf, ich kann schon gar nicht mehr klar denken :).
Jetzt habe ich es geschafft, Shapiro- und Levene-Tests ohne Fehlermeldung hinzubekommen, habe die Ergebnisse auch mittels Histogrammen, QQ-plots und Scatter-Plots angeschaut und mich gefreut, dass es nachvollziehbar scheint… jedoch zweifle ich jetzt daran, ob ich überhaupt die richtigen Daten angeschaut habe. Denn: ich habe quasi alle Daten einer „Messung“ reingepackt (in meinem Fall also z.B. alle Werte zu yield y), nicht aber unterschieden nach verschiedenen Bodenbearbeitungen bb (y~bb). Meine Frage wäre damit, was genau muss jetzt normalverteilt sein, die y innerhalb einer bb (dann womöglich auch unterschieden nach versch. Sorten s), also quasi die kleinste Einheit an Messwerten, wo alle Bedingungen gleich sind. Oder die gesamte Menge an Daten zu einer Messung (hier y), inklusive verschiedener bb und s? Und wenn jetzt die gesamte Datenreihe normalverteilt ist, dann heißt das ja womöglich nicht, dass die Gruppen darin auch normalverteilt sind, oder? *seufz*
Bei manchen Datenreihen ist es außerdem der Fall, dass durch die Transformation der p-Wert für Normalverteilung besser (höher), der für Homoskedaskizität aber schlechter (kleiner) wird. Welche Entscheidung wäre da angebracht?
Über eine Antwort freue ich mich sehr! =)
Annika
Hallo Annika,
zur ersten Frage: Welche Werte müssen auf Normalverteilung überprüft werden? Es muss die Normalverteilung für die Werte überprüft werden, die später im Test zusammen in einer Gruppe sind. Also, wenn später ein Unterschied zwischen den verschiedenen Bodenbearbeitungen untersucht werden soll, dann muss auch die Normalverteilung gruppiert nach Bodenbearbeitung (also für jede Bodenbearbeitung einzeln) untersucht werden. Wenn (z.B. in einer mehrfaktoriellen ANOVA) beide Faktoren Bodenbearbeitung und Sorte angeschaut werden, dann muss auch für diese kombinierte Gruppierung getrennt nach Normalverteilung untersucht werden. Also für Bodenbearbeitung 1 und Sorte A, dann für Bodenbearbeitung 1 und Sorte B, dann Bodenbearbeitung 2 und Sorte A usw.
Zur zweiten Frage: Nach Transformation ist Normalverteilung besser, aber Homoskedastizität schlechter. Hier würde ich die QQ-Plots anschaun. Verbessern die sich durch Transformation? Dann würde ich die transformierten Werte verwenden. Wenn sich bei den QQ-Plots nicht viel tut, aber die Homoskedastizität darunter leidet, würde ich die Transformation nicht machen.
Ich hoffe, die Antworten helfen etwas 🙂
Schöne Grüße
Daniela Keller
Liebe Frau Keller,
Sie haben mir auf jeden Fall sehr geholfen!
Vielen vielen Dank!
Annika
Hallo Frau Keller,
ich habe 25 bzw. 40 Messdaten, die ich auf Normalverteilung prüfen möchte,um dann entspr. Tests anwenden zu können. Sie empfehlen die graphische Beurteilung mittels Q-Q-Plot, wie ich eben gelesen habe. Ich habe bisher den Kol.-Sm.-Test, den Shapiro-Wilk-Test und den Jarque-Bera-Test durchgeführt (per XLSTAT). Der K-S-Test hat ein p-Wert von fast 0,4, die anderen beiden einen p-Wert < 0,05. Zuvor hatte ich auch ein Histogramm erstellt, dieses hat m.E. gar nichts mit einer NV zu tun, da die Daten sehr linksschief vrteilt sind (viele Messwerte sind 0). Was raten Sie mir?
Vielen Dank schon mal!! Ihre Erklärungen hier sind superverständlich, die obige Übersicht drucke ich mir für meine Unterlagen aus, klasse!
VG
Regine
Hallo Regine,
ja, die Tests können sich widersprechen. Das Histogramm ist leider selten hilfreich. Wenn viele Messwerte 0 sind, spricht das aber schonmal gegen eine Normalverteilung. Ich würde hier wieder die Q-Q-Plots empfehlen.
Schöne Grüße
Daniela Keller
Guten Tag! Wenn ich für nicht normalverteilte Daten einen Mann-Whitney-U test mache und die Daten als Balkendiagramm darstellen möchte, was mache ich dann mit der Standardabweichung?
Hallo Laura,
wenn Sie die Mittelwerte der Daten als Balkendiagramm darstellen möchten, dann verwenden Sie für die Fehlerbalken wie gewohnt die Standardabweichung. Auch, wenn die Daten nicht normalverteilt sind. Allerdings empfehle ich hier die Verwendung von Boxplots statt Balkendiagrammen. Boxplots zeigen den Median, die Quartile und Ausreißer, siehe auch dieser Blogbeitrag.
Vielen Dank für die Übersicht, uch hatte eine Erklärung gesucht, was eine nichtparametrische Korrelation ist. Christian
Ich bin Sozialwissenschaftler und in der Statistik eher Anwender, sodass ich mit der mathematischen Seite eher nicht so vertraut bin. Daher eine Verständnisfrage meinerseits:
In der Praxis kommt es häufig vor, dass parametrische Tests, wenn sie auf nicht-parametrische Daten angewendet werden, oft die selben Ergebnisse liefern wie nicht-parametrische Tests. Oft ist es ja nun so, dass die parametrischen Tests genauere und besser interpretierbare Ergebnisse liefern als die Nicht-parametrischen. Daher meine Frage ob es nicht auch zulässig in so einem Fall, in dem beide Tests zum selben Ergebnis kommen, den paramtetrischen Test für nicht-parametrische Daten zu verwenden und nur anzumerken, dass das Ergebnis durch den nicht-parametrischen Test gestützt wird?
Wie gesagt – das ist die Frage einer Anwenderin und ich wäre froh um eine Erklärung!
Vielen Dank 🙂
Gegenfrage: Wenn beide Tests zum selben Ergebnis führen, was spricht dagegen, das Ergebnis des nichparametrischen Tests zu verwenden?
Inwiefern liefern parmetrische Tests „genauere und besser interpretierbare Ergebnisse“?
Die nichtparametrischen Tests sind, wenn sie auf parametrischen Daten verwendet werden, genauso scharf wie die parametrischen Tests in diesem Fall. Mit einem nicht-parametrischen Tests macht man also nichts falsch. Die parametrischen Verfahren haben den Vorteil, dass sie auch bei komplexeren Modellen eingesetzt werden können (mehrere Faktoren…).
Hallo Daniela,
ich hätte eine Frage zu Q-Q Diagrammen. Meine Ausgabe bei SPSS zeigt mir immer ein Q-Q Diagramm (in dem die Punkte sehr schön auf einer Gerade liegen) und ein trendbereinigtes Q-Q Diagramm (in dem ein großes Durcheinander herrscht) an. Nun weiß ich nicht recht wie ich vor allem das trendbereinigte Diagramm interpretieren soll. Könntest du mir vielleicht einen Tipp geben?
Grüße und einen schönen Abend noch.
Hallo Marja,
das erste Diagramm mit der Diagonalen Linie ist das richtige. Das gilt es zu interpretieren. Für das zweite, das trendbereinigte Diagramm, wird die Diagonale gekippt und hineingezoomt. Dadurch kann man sich die Abweichungen von der Diagonalen nochmal genauer ansehen. Für die Entscheidung, ob normalverteilt oder nicht, ist aber das erste Diagramm mit der Diagonalen relevant. Das trendbereinigte kann man getrost ignorieren.
Schöne Grüße
Daniela
Guten Tag!
Ich habe eine Frage zur Normalverteilung von Daten. Ich würde gerne Korrelationstests berechnen (Pearson) und dafür müssen die Daten ja auch normalverteilt sein. In meinem Datensatz sind die Daten NICHT normalverteilt. Ich glaube der Grund ist in einer nicht repräsentativen Stichprobe zu sehen, was mir Bodeneffekte eingebracht hat. Allerdings ist der verwendete Test in repräsentativen Stichproben normalverteilt. Kann ich jetzt trotzdem den parametrischen Korrelationstest nehmen, oder muss ich auf Spearman umsteigen? Anders formuliert: Müssen die Daten nur in ihrer Grundgesamtheit normalverteilt sein, oder auch in der vorliegenden Stichprobe?
Wäre es in meinem Fall erlaubt, alle Werte oberhalb von 2 Standardabweichungen über dem Median als Extremwerte zu löschen (als eine Art Ausreißerbereinigung)? Wenn ich das nämlich tue, sind die Daten gerade so normalverteilt (mit dem Kolmogorov-Smirnov-Test)…
Über eine Antwort würde ich mich sehr freuen!
Herzliche Grüße,
Anna
Hallo Anna,
die Stichprobe sollte normalverteilt sein.
Die Ausreißerbereinigung durch Abschneiden würde ich nicht empfehlen. Ich würde eher anstatt der Tests auf Normalverteilung die Quantilplots betrachten, die sind nicht so streng. Vielleicht kannst Du anhand derer die Normalverteilung annehmen.
Falls das auch nichts bringt: Warum willst Du nicht auf Spearman umsteigen? Der ist (fast) genauso gut wie der Pearson, wenn es nur um bivariate Korrelationen geht.
Hilft das?
Schöne Grüße
Daniela
Ist es richtig, dass der Mittelwert bei nicht-normalverteilten Daten nicht erlaubt ist, sondern nur der Median?
Ist es möglich in einer Doktorarbeit den Mittelwert und den Median bei nicht-normalverteilten Daten zu verwenden und dann die mit nicht-parametrischen Tests zu untersuchen ?
wäre sehr dankbar über eine kurze Antwort
schöne Ostern
Ja, der Median ist bei nicht-normalverteilten Daten besser, da er nicht anfällig für Ausreißer ist und eine eventuelle Schiefe der Daten berücksichtig. Wenn die Daten keine Ausreißer haben und nicht schief sind, ist der Mittelwert auch dann OK, wenn die Daten nicht normalverteilt sind.
Im Zweifel ist es immer sinnvoll, sowohl Mittelwert als auch Median anzugeben und die nicht-parametrischen Methoden zu verwenden.
Ja, das ist möglich und eine gute Lösung.
Hallo zusammen,
ich habe folgende Situation: 3 (Interventionsgruppen) mit 5 Messzeitpunkten. Im Grunde also eine unabhängige sowie eine abhängige Situation mit gleicher Gewichtung. Welcher Test ist der Richtige ? Ich bräuchte somit eine „Mischung“ aus Kruskal-Wallis und Friedman. Kann mir bitte jemand helfen ?
VG Diana
Hallo Diana,
im parametrischen Fall wäre das ein Split-Plot Design. Dafür müssen aber ein paar Voraussetzungen gelten: Normalverteilung in den Gruppen, Homogenität der Varianzen, Spherizität… Wenn das nicht grob verletzt ist und die Fallzahl nicht zu klein ist, kannst Du das verwenden (in SPSS z.B. über Analysieren -> Allgemeines Lineares Modell -> Messwiederholung). Falls die Fallzahl viel zu klein ist oder die Voraussetzungen nicht erfüllt sind, würde ich mir die Daten zunächst deskriptiv ansehen (Mittelwert, Median, Streuung, Abbildungen) und dann je nach Fragestellung einzelne Aspekte mit Tests betrachten (z.B. die Gruppen für jeden Zeitpunkt einzeln vergleichen, oder Differenzen (letzter minus erster Zeitpunkt) für die Gruppen vergleichen oder…).
Schöne Grüße
Daniela
Gut erklärt! Vor allem der Hinweis gefällt mir, dass Normalverteilungstests oft zu streng („konservativ“) sind. Beim t-Test gibt es übrigens die Aussage, dass er laut Monte-Carlo-Studien bei Verletzungen seiner Voraussetzungen recht robust reagiert. Da kann man sich auf Jürgen Bortz berufen (Statistik für Human- und Sozialwissenschaftler).
Danke für die Ergänzung!
Schön erklärt. Vielen Dank 🙂 Und was macht man, wenn man zwei unabhängige SP hat, von denen eine normalverteilt und die andere nicht normalverteilt ist? 🙁
Wenn beide gemeinsam in einem Test untersucht werden, dann nimmt man den nichtparametrischen Test. Nichtparametrische Tests sind grundsätzlich auch auf normalverteilten Daten erlaubt. Sie haben nur eine etwas geringere Teststärke, deshalb sind parametrische Tests wenn möglich (= alle Variablen normalverteilt) vorzuziehen.