Will man einen Zusammenhang zwischen zwei metrischen Variablen untersuchen, zum Beispiel zwischen dem Alter und dem Gewicht von Kindern, so berechnet man eine Korrelation. Diese besteht aus einem Korrelationskoeffizienten und einem p-Wert. Der Korrelationskoeffizient gibt die Stärke und die Richtung des Zusammenhangs an. Er liegt zwischen -1 und 1. Ein Wert nahe -1 bezeichnet einen starken negativen Zusammenhang. Ein Wert nahe 1 spricht für einen starken positiven Zusammenhang. Kein Zusammenhang besteht, wenn der Wert nahe 0 liegt. Der p-Wert sagt aus, ob der Korrelationskoeffizient sich signifikant von 0 unterscheidet, ob es also einen signifikanten Zusammenhang gibt. Meistens werden p-Werte kleiner als 0,05 als statistisch signifikant bezeichnet. Es gibt verschiedene Korrelationskoeffizienten, die bei unterschiedlichen Daten eingesetzt werden. Ich stelle hier den Pearson-Korrelationskoeffizienten und den Spearman-Korrelationskoeffizienten vor.
Du willst mehr Durchblick im Statistik-Dschungel?
Der Pearson-Korrelationskoeffizient wird verwendet, wenn die Daten normalverteilt sind und wenn es einen linearen Zusammenhang zwischen den beiden Variablen gibt. Wie die Normalverteilung überprüft werden kann finden Sie in diesem Beitrag zu Normalverteilungsplots. Den linearen Zusammenhang checken Sie am besten mit einem Streudiagramm. Hier wird die eine Variable an der x-Achse, die andere an der y-Achse angetragen. Im Bild können Sie sehen, ob es einen linearen Zusammenhang zu geben scheint. Sie können außerdem schon erkennen, ob der Zusammenhang positiv oder negativ ist und ob es überhaupt einen deutlichen Zusammenhang gibt. Wenn die Daten nicht normalverteilt sind und/oder der Zusammenhang nicht linear ist, verwenden Sie die Spearman-Korrelation. Diese errechnet sich nicht direkt aus den Messungen, sondern aus den Rängen der Daten. Dadurch kann sie auch nicht-lineare Zusammenhänge erkennen und ist nicht auf normalverteilte Daten beschränkt.
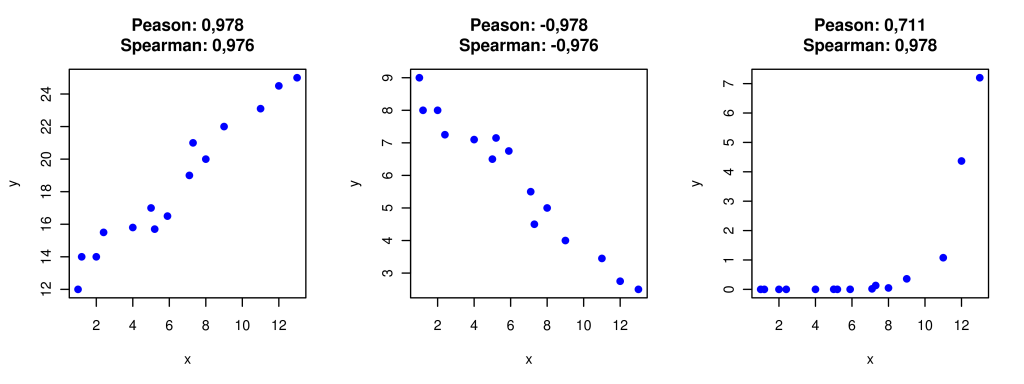
Beide Methoden liefern Ihnen wie oben beschrieben einen Korrelationskoeffizienten für die Stärke und Richtung des Zusammenhangs sowie den p-Wert für die Signifikanz. Wie bei allen statistischen Verfahren ist es hilfreich, sich zusätzlich eine Abbildung anzusehen. In diesem Fall ist die passende Abbildung ein Streudiagramm, das den Zusammenhang anschaulich präsentiert.
Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.
Guten Tag!
Vielen Dank für die Erklärung.
Wie berechne ich denn den p-Wert?
Vielen Dank
Hallo,
der p-Wert wird vom Statistikprogramm gemeinsam mit dem Korrelationskoeffizienten ausgegeben. Wenn Sie ihn selbst ermitteln wollen, müssen Sie aus dem Korrelationskoeffizienten und der Stichprobengröße die Testgröße bestimmen, siehe Formel z.B. hier: http://www.faes.de/Basis/Basis-Statistik/Basis-Statistik-Korrelation-Re/Basis-Statistik-K-R-t-Test/basis-statistik-k-r-t-test.html Diese Testgröße (hier im Link PG genannt) ist t-verteilt. Über Tabellen zur t-Verteilung (siehe auch dort im Link) können Sie dann den p-Wert ermitteln.
Schöne Grüße
Daniela Keller
Hallo!
Vielen Dank für den tollen Artikel.
Wenn ich nun aber zwei oder mehrere Korrelationskoeffizienten aus einer abhängigen Stichprobe vergleichen möchte, wie gehe ich hier vor?
Und wie kann ich das Ergebnis dann interpretieren?
Dankeschön
Hallo,
wie Sie Korrelationskoeffizienten vergleichen können, habe ich hier beschrieben: https://statistik-und-beratung.de/2013/06/korrelationen-vergleichen/
Schöne Grüße
Daniela Keller
Vielen Dank! Sie haben mir sehr geholfen.
Jetzt hätte ich noch eine Frage.
Ich habe einen Test mit 2 verschiedenen Untertests, die ich miteinander korrelieren möchte. Je nach Altersgruppen können die Probanden verschieden viele Punkte in den 2 Untertests erreichen.
So kann z.B. Altersgruppe X im Untertest 1 11 Punkte erreichen und im Untertest 2 19 Punkte erreichen. Im Gegensatz dazu kann Altersgruppe Y im Untertest 1 nur 7 Punkte erreichen und im Untertest 2 nur 14 Punkte erreichen.
Wenn ich jetzt die beiden Untertests miteinander korrelieren möchte und dabei die Ergebnisse aller Altersgruppen einfließen lassen möchte, kann ich dann die Zahlen einfach so lassen und korrelieren? Oder muss ich den Höchstpunktezahl einer Altersgruppe fix annehmen und die Punkte der anderen Altersgruppen dann hochrechnen?
Bsp: U1 U2
Altersgruppe X 9 15
8 16
Altersgruppe Y 6 12
5 11
Kann ich das einfach so korrelieren oder muss ich Altersgrupe Y hochrechnen (siehe unten)
Bsp: U1 U2
Altersgruppe X 9 15
8 16
Altersgruppe Y 9.428 16.285
7.857 14.928
Oder muss ich nur diese Zahlen miteinander korrelieren?
Vielen Vielen Dank
Hallo,
Sie müssen die Zahlen pro Untertest anpassen, so dass die Probenden unabhängig von der Altersgruppe die gleiche Zahlenspanne im Untertest erreichen können. Genauso, wie Sie es in den Beispielen vorgeschlagen haben.
Anschließend können Sie mit den so normierten Zahlen eine Korrelation zwischen U1 und U2 berechnen.
Schöne Grüße
Daniela Keller
Hallo Frau Keller!
Kompliment an die schlichte Eleganz der Website und Ihre klaren, auf den Punkt gebrachten Erklärungen hier. Auf der Suche nach Antworten zu einigen statistisch-methodischen Fragen im Psychologiestudium bin ich auf diesen Blog gestossen. Ich hätte auch noch eine Frage, und zwar wie man eine quasi ungerichtete Zusammenhangshypothese am besten statistisch testet. Also eine Hypothese der Form „Unterschiede in Variable X (z.B. Selbstwirksamkeit) gehen mit Unterschieden in Variable Y (z.B. Nutzung von Lernstrategien)“ einher. Es handelt sich also nicht um eine gerichtete Hypothese, in dem Sinne, dass hohe Ausprägungen der ersten Variable mit hohen/niedrigen Werten der zweiten Variable einhergehen, sondern das wird offengelassen. Kann man so eine Hypothese sinnvoll statistisch testen oder wäre eine solche Hypothese an sich problematisch? Wenn ersteres der Fall ist, was würde man am besten machen? F-Test auf Varianzunterschiede? Vielleicht mit künstlicher Dichotomisierung der ersten Variable oder so etwas?
Viele Grüße!
Hallo Matthias,
schön, dass Ihnen mein Blog gefällt!
Zu Ihrer Frage: Eine ungerichtete Zusammenhangshypothese wird ganz klassisch mit der Korrelation berechnet. Hier wird untersucht, ob zwei Variablen zusammenhängen. Die Nullhypothese ist „Es gibt keinen Zusammenhang“. Die wird mit einem signifikanten p-Wert abgelehnt. Über das Vorzeichen des Korrelationskoeffizienten sehen Sie dann, in welche Richtung der Zusammenhang geht. Das nennt sich zweiseitiges Testen und ist in den allermeisten Fällen sinnvoll. Alternativ könnte man auch einseitig testen, dann wird nur in eine Richtung geschaut. Das macht aber nur Sinn, wenn ein Zusammenhang in die andere Richtung völlig undenkbar ist, und das ist meist nicht der Fall. Auch wenn Ihre Forschungsfrage gerichtet wäre, würden Sie also zweiseitig testen. Die Nullyhpothese wäre also trotzdem die gleiche wie oben genannt.
Herzliche Grüße
Daniela Keller
Herzlichen Dank für Ihre Anwort! Da hab ich wohl wegen der Idee, künstliche Gruppen zu machen, zu kompliziert gedacht.
Trotz der etwas ungewöhnlichen Formulierung der Hypothese handelt es sich ja um eine ungerichtete Zusammenhangshypothese.
Hallo Frau Keller,
ich versuche bei meiner Arbeit eine statistische Analyse zwischen einem Indix von Radiosondendaten und einer Dachstatition zu machen. Da hab ich durchgehend bei der Pearsonkorrelation Werte zwischen 0.06 und 0.15 (7 Ergebnisse mit jeweils anderem Index). Bei den gleichen Indices bekomm ich bei Kendall und Spearman Werte zwischen 0,6 und -0,6. Allein durch das Ergebnis würde ich die zuletzt genannten Korrelationen da ich eine deduktive Rangehensweise ausgesucht habe. Aber mich verwundert es, dass die Ergebnisse zwischen P und K/S so stark abweichen. Woran könnte das liegen? PS: Die Datensätze sind so groß, dass ich keine Streudiagramm machen kann um eine Signifikanz vorher schon zu erkennen.
Viele Grüße
Hallo, es könnte sein, dass ein nicht-linearer Zusammenhang vorliegt. Den kann Pearson nicht so gut aufdecken wie Spearman oder Kendall. Zudem sollten Sie Pearson nur verwenden, wenn die Daten annähernd normalverteilt sind. Sind sie das? Wieso sind die Datensätze zu groß für ein Streudiagramm?!?
Schöne Grüße
Daniela
Liebe Frau Keller,
vielleicht können Sie mir eine Empfehlung für das weitere Vorgehen geben.
Ich untersuche drei Gruppen, bei denen vier Messungen vorliegen. Eine Gruppe vor einer Intervention und eine nach dieser Intervention. Zusätzlich habe ich eine KG (ohne Intervention) und eine Gruppe, deren Intervention lange zurück liegt.
Wenn ich jetzt die Interkorrelationen meiner verendeten Skalen berichte, dann kann ich diese doch nicht für alle vier Messungen gemeinsam berichten? (Weil sonst ein Teil der Personen zweimal in der Berechnung auftaucht). Sehe ich das richtig, dass ich dann nur die Werte von der KG, der lange-ist -es-her-Gruppe und der Werte der Interventionsgruppen zu einem Zeitpunkt berichte? Wenn ja, dann zu Zeitpunkt 1 oder 2? Oder getrennte Interkorrelationen für alle vier Gruppen?
(Die gleiche Frage stellt sich auch für die Berechnung von Cronbach Alpha)
Danke und viele Grüße
Johannes
Lieber Johannes,
das haben Sie richtig eingeschätzt: Es darf keine Person mehrmals vorkommen. Also die eine Mehrfachmessung heraus lassen (welcher ist meiner Ansicht nach egal), oder jede Gruppe und Messzeitpunkt einzeln untersuchen, das geht auch. Für Cronbachs Alpha genauso.
Nutzen Sie doch die Facebook-Gruppe Statistikfragen für weitere Fragen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela Keller
Liebe Frau Keller,
mir gefällt ihr Blog sehr gut und hat mir schon viel geholfen.
Im Rahmen einer Studienarbeit möchte ich gern den Zusammenhang Alter und Onlinebuchungen untersuchen. Dazu habe ich die Hypothese “ Je jünger ein Teilnehmer desto mehr Reisen bucht er im Internet“ aufgestellt. Das Alter habe ich in meiner Umfrage in Altersklassen abgefragt (18-25 Jahre, 26-…) die Häufigkeit ebenfalls in Gruppen (Wie viele Reisen buchen Sie online: keine, die wenigsten, die meisten, alle.)
Können Sie mir hier weiterhelfen. Welche statistischen Verfahren kann ich denn zur Untersuchung der Hypothese verwenden?
Liebe Grüße
Kristina
Hallo Kristina,
das kannst du mit einer Kreuztabelle untersuchen. Dort kannst du die Häufigkeiten in den einzelnen Kombinationen der Altersklassen und der Buchungsklassen beschreiben und siehst damit deskriptiv, wie der Zusammenhang ist.
Ob der Zusammenhang signifkant ist, sagen dir dann die Tests dazu. Der klassische Chi-Quadrat-Test schaut, ob es überhaupt einen Zusammenhang gibt. Der Test auf linearen Zusammenhang schaut, ob es eben einen linearen gibt. Der würde bei deiner Fragestellung auch passen.
Schöne Grüße
Daniela
Hallo Frau Keller,
tolle Seite, einfach erklärt und super verständlich. Große Hilfe.
Bzgl. einer Studienumfrage habe ich zwei Selbstbeschreibungen generiert. Per Zufall wurden die Probanden dann entweder der neg. oder der pos. zugeordnet. Im Anschluss an das lesen der Beschreibung wurde als Manipulationscheck jeweils eine Frage, die auf einer 5 Punkte Likert Skala von 1 (überhaupt nicht) bis 5 (äußert) zu beantworten galt, zu einer von drei Dimensionen abgefragt.
Mich interessiert, ob die drei abgefragten Dimensionen in der neg. Beschreibung gut dargestellt wurden oder besser als in der pos. Beschreibung (Da bin ich mir Unsicher wie man es richtig formuliert oder macht).
Welches statistische Verfahren muss ich jetzt anwenden um eben diese Zusammenhänge oder Unterschiede zu erhalten.
Vielen Dank
Lg
Nina
Hallo Nina,
du willst also jede Skala für einen Unterschied zwischen den beiden Gruppen positiv und negativ unterscheiden, oder? Wenn die Skala nicht normalverteilt ist, dann ist das der Mann-Whitney-U Test.
Sieh dir doch mein E-Book an. Das gibt es kostenlos zum Download hier auf meiner Seite. Da findest du die wichtigsten Methoden beschrieben und eine Übersicht, die dir hilft, die richtige Methode auszuwählen.
Schöne Grüße
Daniela
Hallo Frau Keller,
vielen Dank für die tollen Erklärungen! Die haben mir schon wirklich weitergeholfen!
Aber ich schreibe gerade an meiner Abschlussarbeit und bin noch ein wenig unsicher.
Ich habe eine Umfrage durchgeführt und SPSS (ich bin da noch nicht so fit drin) spuckt mir fast nur ordinale und nominale Variablen aus.
Bisher habe ich nur Kreuztabellen erstellt. (Bsp: Vergleich Geschlecht und Einkaufsverhalten – mit der Frage „Gehen Frauen öfter Shoppen als Männer?“) Wären in dem Fall auch Korrelationen sinnvoll?
Über eine Antwort würde ich mich sehr freuen!
Liebe Grüße
Hallo Sandra,
SPSS sollte dir nicht das Messniveau vorgeben. SPSS rät das nur. Du kannst es aber anpassen, wenn SPSS falsch geraten hat (in der Variablenansicht in der Spalte Maß).
Wenn das Einkaufsverhalten mehrere Ausprägungen hat (z.B. 5), wäre auch ein Test auf Lageunterschied (Mann-Whitney U) möglich, um Männer und Frauen im Einkaufsverhalten zu vergleichen. Wenn es weniger Ausprägungen hat, passt die Kreuztabelle. Korrelationen sind nur bei zwei ordinalen oder metrischen Variablen sinnvoll.
Schöne Grüße
Daniela
Hallo Frau Keller,
ich habe ebenfalls eine Frage.
Bei der Faktorenanalyse ist es wichtig, dass die Variablen normalverteil sind, oder?(damit ist ein Zusammenhang der Variablen zu erklären)
Die sich daraus ergebende Frage ist, wieso die Nullhypothese wie folgt heißt „Die Variablen sind NV“ und die H1 „Die Variablen sind nicht NV“.
Ich dachte immer, dass die H0 verworfen werde muss. Wieso wird hier bei einem guten Fall (also bei NV der Variablen) die H0 angenommen und die H1 verworfen?
Auf Ihre Rückmeldung würde ich mich sehr freuen.
Hallo,
für die Faktorenanalyse müssen die Variablen nicht normalverteilt sein. Eine Normalverteilung (oder zumindest symmetrische Verteilung) begünstigt aber lineare Zusammenhänge zwischen den Variablen, die widerum gut für die FA sind.
Die Tests auf Normalverteilung prüfen die Nullhypothese „Die Variablen sind normalverteilt“. Das liegt an der Art des Tests, geht nicht anders. Deshalb will man hier bei der Prüfung der Normalverteilung einen großen p-Wert (größer als das Signifikanzniveau), um annähernde Normalverteilung nachzuweisen und die H0 eben nicht zu verwerfen.
Schöne Grüße
Daniela
Liebe Frau Keller,
erstmal ein großes Lob an Ihren Blog. Sie enthalten bis jetzt die einzigen leicht verständlichen Beiträge zu statistischen Berechnungen, welche im Internet zu finden waren. Ich verstehe nun zumindest, wie sich die einzelnen Kennzahlen zueinander verhalten.
Ich hätte auch eine Frage:
Ich möchte berechnen, ob die Anzahl von Youtube-Views eine bestimmten Videos mit den Google-Suchanfragen zu einem bestimmten Begriff und dem Traffic einer Website signifikant korreliert.
Muss ich etwas besonderes beachten, z.B. ist Pearson oder Spearman besser geeignet?
Und…
Wenn der Websitetraffic in einem Monat einen besonders hohen Ausschlag hat im Vergleich zum Rest des Jahres, möchte ich berechnen, ob dieser signifikant ist. Ist dazu ein einseitiger t-test geeignet?
Ich würde mich sehr über eine Antwort freuen.
Besten Gruß
Hallo Florian,
danke für das Lob 🙂
Ob Pearson oder Spearman besser passt hängt davon ab, ob die Messwerte normalverteilt sind oder nicht und ob der Zusammenhang linear ist. Bei Pearson sollten die Messwerte normalverteilt sein und es sollte ein linearer Zusammenhang gegeben sein. Alternativ dann Spearman verwenden.
Für den Test auf signifikanten Unterschied passt der Einstichproben t-Test, wenn du einen festen Wert hast, zu dem du vergleichen willst. Dann kannst du die Messwerte dieses einen Monats zu diesem festen Wert vergleichen. Falls die Messungen nicht normalverteilt sind, ist das hier statt des Einstichproben t-Tests der Einstichproben Wilcoxon-Test. Wenn du keinen festen Wert hast, sondern mehrere Monate vergleichen willst (z.B. 12 Monate), verwendest du bei Normalverteilung die ANOVA, ansonsten den Kruskal-Wallis Test. Diese beiden sagen dir dann, ob insgesamt ein Unterschied zwischen den Messreihen besteht. Wo der Unterschied liegt, sagen sie dir nicht. Dafür wären dann paarweise Post-Hoc Tests notwendig.
Schöne Grüße
Daniela
Liebe Frau Keller,
Ich möchte den Zusammenhang zweier Variablen (einem Konstrukt aus dem Emotions und Erfahrungsbereich) berechnen. Mein Problem: die beiden haben in dem Streuungsdiagram absolut keinen linearen Zusammenhang. Die kleinen Werte auf der x-Achse sind auf der y-achse sehr hoch und mittel hoch, da zieht es sich der y-achse entlang hinauf bis zum max. Wert und ist ziemlich dicht.die größeren x-achse werte sind sehr groß auf der y achse und relativ wenige. Würde man es mit einer linie nachzeichnen wäre es ein halbes T ( nur die rechte seite vom T).
Wie kann ich einen Zusammenhang berechnen?
danke!
Hallo Gaby,
die Spearman-Korrelation geht auch für nicht-lineare Zusammenhänge. Die müsste hier passen.
Schöne Grüße
Daniela
Hallo Frau KelEler,
ich habe ebenfalls eine Frage.
Die Anpassungslinie in meinem Streudiagramm ist nahezu horizontal. Bei R2 steht: R2= 2,190E-4
und
auf der Linie: y=6E2+0,91
Was bedeutet dieses E und was mache ich mit einem Wert R2 der größer als 2 ist?
Beste Grüße und vielen Dank
Hallo Chris,
das E bedeutet „mal 10 hoch“. ALso 2,190E-4 ist „2,190 mal 10 hoch -4“. Das ist folgende Zahl ausgeschrieben: 0,000219. Der R2 ist also nicht 2, sondern fast 0.
Schöne Grüße
Daniela
Guten Abend Frau Keller,
warum darf man den Korrelationskoeffizienten von Pearson bei nicht normalverteilten Zusammenhängen nicht verwenden?
Vielen Dank!
Chris
Hallo Chris,
wenn man den Test dazu verwendet (also den p-Wert interpretieren will, der aussagt, ob sich der Korrelationskoeffizient signifikant von 0 unterscheidet), dann benötigt man normalverteilte Daten, da diese Berechnung beim Pearson auf Normalverteilung basiert.
Schöne Grüße
Daniela
Hallo Daniela,
habe die Normalverteilung zweier Fallgruppen mit mittels Kolmogorof-Smirnov-Test durch Software SPSS® überprüft. Für die eine Gruppe wurde ein Wert der asymptotischen Signifikanz von .047 angegeben und die Gruppe als normalverteilt bezeichnet. Das verwirrt mich, da p < .05 eigentlich eine signifikante Abweichung von der Normalverteilung bedeutet?? Kannst du mir dazu was sagen…..???
Hallo Timo,
je nachdem, welches Signifikanzniveau du dir zugrunde legst, ist bei p=0,047 die Gruppe nicht normalverteilt (wenn alpha=0,05) oder normalverteilt (wenn alpha=0,01, zum Beispiel).
Schöne Grüße
Daniela
Guten Abend Frau Keller,
mir gefällt Ihre Blog sehr gut und finde die Antworten die Sie geben sehr leicht verständlich und komme daher mit einer Frage zu Ihnen!
Im Rahmen einer Forschungsarbeit vergleiche ich gerade Werte einer Testgruppe.
1. Es gilt Zusammenhänge zwischen zwei verschiedenen Variablen aufzuzeigen per SPSS-Korrelation. Die eine ist jedoch nominal skaliert mit den Endwerten „1“ und „0“ für vorhanden/nicht vorhanden, die Andere ist verhältnisskaliert mit Werten von 0-100 („Skala“ in SPSS).
Ist eine solche Operation überhaupt möglich und die Werte interpretierbar?
Hallo Aeneas,
hier kannst du die punktbiseriale Korrelation verwenden. Die gibt es nicht ausdrücklich in SPSS, wenn du aber mit diesen beiden Variablen die Spearman-Korrelation berechnest, bekommst du als Ergebnis die punktbiseriale Korrelation (da die Formel identisch ist).
Schöne Grüße
Daniela
Hallo Frau Keller,
auch ich muss zunächst einmal ein dickes Lob für die Seite loswerden. Danke für die vielen verständlichen Beiträge!
Nun meine Frage, ebenfalls zur Korrelation: Da mein Datensatz nicht normalverteilt ist, nutze ich die Spearman-Korrelation. Der Test auf Signifikanz ergibt bei mir stets ,000. Könnten Sie mir ganz simpel erklären, was das bedeutet? Ist das „ok“ oder eine Art Sonderfall? Herzlichen Dank vorab!
Viele Grüße, Kerstin
Hallo Kerstin,
wenn die Software (ich vermute es ist SPSS) ,000 ausgibt, dann verwendest du „<,001". Der p-Wert kann nie genau 0 sein. Aber er ist in diesem Fall dann sehr klein, hat so viele Nuller, dass SPSS das nicht mehr alles aufschreibt. Deshalb verwendet man dann "p<0,001". Schöne Grüße Daniela
Hallo Frau Keller,
Erst einmal: super Seite, und absolut hilfreich,vor allem wenn keiner sonst weiter weiß.
Ich bräuchte nun auch Hilfe.
Wie kann ich Werte imputieren?
Im konkreten: Ein Fragebogen von 109 Fragen wurde ca 100 Personen vorgelegt. Es fehlte aber,bei allen, die 110te Frage, die wurde unabsichtlich nicht gestellt. Nun möchte ich diese letzte Antwort schätzen, indem ich 10 der Antworten,die zur selben Subskala gehören wie die fehlende,als Prädiktor verwenden. Welches Verfahren kann ich nehmen? Stimmt es, dass es sich um einen systemischen Fehler handelt- also es fehlen nicht mitten drin Werte, sondern genau die letzte Antwortreihe.
Vielen Dank,
Ric
Hallo Ric,
Imputation wird normalerweise verwendet, um einzelne fehlende Antworten von Variablen aufzufüllen, nicht, um eine komplette Variable zu erstellen. Dein geplantes Vorgehen kann nur funktionieren, wenn du weißt, wie sich die 110. Frage aus den anderen Fragen zusammensetzt (z.B. als Mittelwert oder gewichtetes Mittel). Da keiner die 110. Frage beantwortet hat, kannst du diese Info nicht aus den Daten bekommen. Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Frau Keller, für meine Masterarbeit habe ich gerichtete Hypothesen aufgestellt. H1 besagt, dass Schüler mit Förderung besser mathematische Kenntnisse erhalten, als Schüler die nicht gefördert werden.
H0 besagt. Schüler mit Förderung unterscheiden sich nicht in den Leistungen zwischen den Schülern, die nicht gefördert werden. Dazu habe ich den t-Test angewendet. Die Schüler der Evaluationsgruppe erhalten hochsignifikant (p= .000) niedrigere Ergebnisse als die der Kontrollgruppe (Rohwert -2,78). Das heißt doch, dass ich weder die H1 noch die H0 annehmen kann???1!! Wenn das so sein sollte, wo finde ich es in der Literatur?
Noch eine Frage: wenn die Varianzhomogenität zwischen den Mittelwerten beider Gruppen nicht gegeben ist, darf ich den t-Test doch nicht rechnen? Gibt es Ausnahmen?
Herzliche Grüße, Anja
Hallo Anja,
du hast die H1 gerichtet formuliert, dann solltest du die H0 auch gerichtet formulieren, damit sie zusammen passen. Damit würdest du dann die H0 nicht ablehnen mit deinem Testergebnis. Bei Varianzheterogenität nimmst du den Welch-Test.
Schöne Grüße
Daniela
Liebe Daniela
Danke für die Möglichkeit hier was zu fragen.
Ich habe einen Mann Whitney U Test gemacht und dabei eine Signifikanz gerechnet. Kann ich dazu nun eine Richtung angeben und wenn ja wie finde ich die raus?
Und noch eine Frage, was ist „k“ in diesem Zusammenhang?
Meine Daten sind so alt und ich habe dummerweise dazu keine Aufzeichnungen gemacht, Daher wäre ich sehr dankbar für eine Antwort.
Vielen Dank
Marie
Hallo Marie,
das ist keine Frage zum Blogbeitrag der Korrelation. Trotzdem hier die Antwort: die Richtung findest du heraus, indem du dir die deskriptiven Werte ansiehst.
Weitere Fragen kannst du gern in meiner Facebookfruppe Statistikfragen stellen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Frau Keller,
zunächst möchte ich Ihnen meinen Dank aussprechen, weil ich es klasse finde, dass Sie hier jegliche Fragen beantworten.
Ich habe ein Problem mit meiner Ausgabe der Korrelation nach Pearson. Alle signifikanten Korrelationen werden mir mit * oder ** angezeigt. Diese sind zu betrachten. Die dazugehörige 2-seitige Signifikanz ist dabei aber immer (bei allen 32 Fällen) p=.000. Die Dame zuvor hatte die selbe Frage zur Spearman-Korrelation… Ist es bei der nach Pearson genauso, oder liegt ein Fehler vor?
Liebe Grüße
Eva
Hallo Eva,
wenn SPSS p=.000 ausgibt bedeutet das p<.001. Egal bei welchem Test. Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Frau Keller!
Ich möchte gerne mittels partieller Korrelation ausrechnen, ob sich Neurotizismuswerte auf den Zusammenhang von S und P ( ergab eine spearmankorr. von =.28) auswirkt.Also diese N-Werte konstant halten. Kann ich das denn überhaupt, wenn S und P einen nicht linearen Zusammenhang haben? Die Vorraussetzungen der paritellen Korrelation sind doch Homoskedastizität der Residuen und Normalverteilung der Residuen? danke
Hallo Chris,
vielleicht kannst due Homoskedastizität, Linearität und Normalverteilung über geeignete Transformationen erzeugen. Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Guten Tag Frau Keller,
Wäre sehr froh um eine schnelle Antwort:-)
Wenn Pearson 0.223 und Spearman 0.229 ist und bei Sig.(2-seitig) .000 steht, kann ich dann davon ausgehen, dass die Korrelationen statistisch signifikant sind? Oder muss ich einen T-Test machen?
Vielen Dank
Liebe Grüsse
L
Hallo,
ja, das ist signifikant. Wozu hier ein t-Test???
Schöne Grüße
Daniela
Liebe Frau Keller
Bei der Berechnung der Spearman Korrelation erhalte ich zwar Korrelationswerte (welche auch Sinn ergeben), aber bei fast jeder kann ich die H0 nicht verwerfen. Woran könnte das liegen? Die Variablen sind dichotom oder nicht linear verteilt.
Was kann man machen, damit die Korrelationen signifikant werden?
Herzlichen Dank für Ihre Antwort.
Hallo Markus,
Deine Stichprobe ist wohl zu klein.
Weitere Fragen gern in der Facebookgruppe Statistikfragen posten: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
bei meiner Arbeit stoße ich immer wieder auf deine Seite und bin begeistert von den leicht verständlichen Erklärungen.
Jetzt habe ich folgende Fragen:
1.) Mir ist der Unterschied zwischen Korrelation und Regression noch nicht ganz bewusst. Bei zwei Variablen könnte ich doch genauso gut eine Regressionsgerade einfügen, oder? Die Werte wären doch identisch? Ein Beispiel…
2.) Ich möchte zeigen, dass ein neu entwickeltes Gerät genauso gut misst wie bereits bekannte Geräte. Dazu habe ich ein Streudiagramm erstellt, auf der X-Achse ist die neue Methode bzw. das neue Gerät aufgeführt (Messmethode T) und auf der Y-Achse das alte Gerät. Da ich mehrere alte Geräte zum Vergleich heranziehe (Messmethode A, B, C) habe ich diese gemeinsam in ein Streudiagramm eingezeichnet mit unterschiedlichen Punkten in Form und Farbe.
Würde ich jetzt Korrelationskoeffizienten angeben und gar keine Gerade in das Streudiagramm einfügen oder würde ich Regressionsgeraden für die jeweiligen Methoden einfügen und R² angeben?
Danke für deine Arbeit und Mühe, so eine Seite aufzubauen und auch mit so viel Input immer wieder am Leben zu erhalten.
Hallo Lena,
Korrelationen passen immer, wenn man die Zusammenhänge zwischen zwei metrischen Variablen untersucht. Dabei muss keine Annahme über die Richtung des Zusammenhangs getroffen werden.
Regressionen nimmt man dann, wenn man eine Richtung zu Grunde legt, wenn man also entscheidet, was unabhängige Variable (Faktor) und was abhängige Variable ist. Dann untersucht man, wie der Faktor auf die abhängige Variable wirkt. Das Ergebnis kann man dann auch genau so interpretieren (Wie stark ist der Effekt des Faktors auf die abhängige Variable?)
Weitere Fragen gern in der Facebookgruppe Statistikfragen posten: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Liebe Daniela,
während der Recherche für meine Masterarbeit bin ich auf deine Seite gestoßen. Sie hat mir schon viel geholfen mich in die Statistik einzulesen, die mir zuvor recht fremd war.
Mir ist noch etwas unklar, was genau der Unterschied zwischen dem Ergebnis des Spearman-Test und des Mann-Withney-Test bzw. Kruskal-Wallis-Tests ist? In meinem Zusammenhang: Ich habe Daten, die nicht normalverteilt sind und bei denen ich den Zusammenhang der Anzahl der richtigen Antworten bei einem Fragebogen mit verschiedenen Merkmalen bestimmen möchte. Beispielsweise mit dem Geschlecht oder ob eine bestimmte Vorlesung belegt wurde. Ich bin mir nun unsicher welchen Test ich verwenden soll; ob es notwendig ist sowohl den Spearman-Test als auch den Mann-Withney-Test (bzw. bei mehr Ausprägungen den K-W-Test) zu verwenden und wenn ja, worin bei deren Aussagen der Unterschied liegt.
Mit freundlichen Grüßen und einem herzlichen Dankeschön,
Lisa
Hallo Lisa,
Spearman wird für Zusammenhänge zwischen metrischen oder ordinalen Variablen berechnet, Mann-Whitney U ist ein Test für einen Lageunterschied (also wenn eine Gruppenvariable ins Spiel kommt). Genauer erklärt findest Du das in meinem kostenlosen E-Book: https://statistik-und-beratung.de/gratis-e-book-statistische-datenanalyse-die-grundlagen/
Schöne Grüße
Daniela
Hallo Daniela,
ich schreibe gerade meine Masterarbeit und brauche deine Hilfe. Ich habe von mehreren Unternehmen die jährlichen Renditen sowie Aktienkurse am Tag der Dividendenzahlungen über 20 Jahre. Die Berechnung der jeweiligen Pearson-Korrelationskoeffizienten pro Unternehmen habe ich in Excel vorgenommen. An dem Durchschnitt der Korrelationskoeffizienten lese ich den Zusammenhang zwischen der Rendite und den Unternehmenswerten (Aktienkursen) ab.
Wie führe ich nun mit SPSS einen Hypothesen-t-Test durch, um zu sehen, ob mein Korrelationskoeffizient signifikant ist?
Kann ich einfach alle Renditen und Kurse untereinander schreiben, ohne zu beachten, von welchen Unternehmen sie sind?
Herzlichen Dank!
Beste Grüße
Andrea
Hallo Andrea,
Du willst wohl die berechneten Werte (Korrelationskoeffizienten) zum Wert 0 vergleichen (keine Korrelation). Ja, dazu schreibst Du alle untereinander in eine Spalte und führst einen Einstichproben-T-Test durch (sofern Normalverteilung vorliegt).
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo,
was mache ich, wenn ich zwischen zwei metrischen Variablen in SPSS eine Korrelation testen möchte, diese aber im Streudiagramm so überhaupt nicht linear ist? Reicht das allein aus, um zu sagen, dass keine Korrelation vorliegt? Beispiel: ich habe auf der x-Achse das Alter und auf der y-Achse die Höhe eines Blutparameters. Das Streudiagramm zeigt mir vor allem einen nahezu gedacht-vertikalen Strich, der links an der y-Achse klebt. Alle anderen Punkte sind wild verstreut.
LG Franzi
Hallo Franzi,
Du kannst in jedem Fall eine nichtparametrische Korrelation rechnen, auch wenn keine Linearität vorliegt.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Sehr geehrte Frau Keller,
endlich eine Seite, die es auch Laien möglich macht, in das Thema einzusteigen. Danke hierfür.
Im Rahmen meines Studiums berühre ich die Statistik (allerdings habe ich nach meinen bisherigen Recherchen den Eindruck, ich schwimme nur auf der Oberfläche). Ich möchte aber gern verstehen, was ich da lese und lerne, daher nun meine Frage:
Meine Hypothese ist z.B.: Jugendliche, die in schlechten wirtshaftlichen Verhältnissen aufwachsen, werden häufiger straffällig als andere.
Nun weiß ich, dass meine Nullhypothese davon ausgeht, dass kein Zusammenhang zwischen den zwei Variablen besteht, dann vergleiche ich die Verteilung der Nullhypothese mit der tatsächlich in meiner Stichprobe festgestellten Verteilung. Bekomme ich bei der Verteilung ein Ergebnis, das aussagt, dass sie mit über 95%iger Wahrscheinlichkeit auf zufälliger Varianz der Stichprobe basiert, habe ich meine Nullhypothese widerlegt und die Hypothese belegt (ich hoffe, das ist bis hier hin richtig). Es bedeutet also, dass ich mit einer Irrtumswahrscheinlichkeit von weniger als 5% einen Effekt erhalten oder gemessen habe, der so auch in der Population zu finden ist? Das Ganze wird dann ausgedrückt als p<0,05, was wiederum bedeutet, dass mein Effekt signifikant für die Population ist?
Weiter habe ich dann gelesen, dass die Signifikanz noch nichts darüber aussagt, wie stark der Effekt ist, was wäre denn in diesem Fall die Effektstärke (umso so schlechter die wirtschaftlichen Verhältnisse, desto mehr tritt Straffälligkeit auf)? Liegt der Korrelationskoeffizient dann bei +1 habe ich eine vollständige Abhängigkeit der Straffälligkeit von den wirtschaftlichen Verhältnissen, liegt er bei -1 bedeutet das umso schlechter die Verhältnisse, desto weniger Straffälligkeit und bei 0 besteht kein Zusammenhang?
Vielen, vielen Dank bereits im Voraus!!
Viele Grüße
Hallo Sarah,
ja, das hast Du richtig verstanden. Ich versuche es für Dein Beispiel nochmal zu formulieren. Nehmen wir an, Du misst sowohl die Straffälligkeit (Häufigkeit) als auch die Lebensverhältnisse (gut bis schlecht) als metrische oder ordinale Variablen. Dann würdest Du zur Prüfung der Nullhypothese eine Korrelation rechnen. Die Nullhypothese lautet: „Es gibt keinen Zusammenhang zwischen Straffälligkeit und Lebensverhäntissen“. Die Korrelation liefert Dir einen Korrelationskoeffizienten und einen p-Wert. Der p-Wert gibt Dir die Signifikanz. Ist er kleiner als 0,05, so hast Du einen signifikanten Zusammenhang nachgewiesen. Der Zusammenhang zwischen den beiden Variablen unterscheidet sich also signifikant von Null. (Oder: Es ist sehr unwahrscheinlich, diese Daten zu messen, wenn es in Wahrheit keinen Zusammenhang gibt). Der Korrelationskoeffizient ist in dem Fall das Effektstärkemaß, es sagt Dir, wie stark der Zusammenhang ist und in welche Richtung er geht.
Schöne Grüße
Daniela
Hallo Daniela,
deine Seite hat mir für meine Studienarbeit schon sehr geholfen! Ich habe dennoch eine kleine Frage. Wenn ich den Chi²-Test mache und dabei heraus kommt, dass es keinen signifikanten Zusammenhang gibt, gelten dann die Phi bzw. Cramer’s V Werte noch, die angeben, wie stark der Zusammenhang ist?
Zudem habe ich bei einem Phi-Wert einmal ein negatives Ergebnis (-0,15) bekommen. Heißt das, dass ein schwacher negativer Zusammenhang besteht? Wird also die Nullhypothese bestätigt?
Liebe Grüße und vielen Dank
Anna
Hallo Anna,
wenn der p-Wert nicht signifikant ist, kannst Du Phi oder V zumindest beschreibend verwenden. Eventuell ist auch die Fallzahl zu klein, um den Effekt als signifikant nachzuweisen. Je nachdem, in welche Richtung der Zusammenhang geht, kann Phi auch negativ sein.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Guten Tag Frau Keller
Eine Analyse mit SPSS hat ergeben, dass der p-Wert 0.000 beträgt und Kendall Tau b ist 0.3. Es besteht also eine hohe Signifikanz, aber nur ein schwacher Zusammenhang. Meine Interpretation davon ist, dass es sehr Wahrscheinlich ist, dass ein Zusammenhang zwischen den beiden Variablen besteht, aber dass die abhängige Variable noch von weiteren Einflussgrössen beeinflusst wird.
Ist das richtig, oder irre ich mich.
Vielen Dank und liebe Grüsse
Jonathan
Hallo Jonathan,
ja, das ist richtig.
Schöne Grüße
Daniela
Liebe Daniela,
können eigentlich Korrelationskoeffizienten auch interpretiert werden, wenn diese nicht signifikant sind?
Schonmal herzlichen Dank für Deine Antwort
Johanna
Hallo Johanna,
ja, aber dann nur deskriptiv und mit Vorsicht denn es ist dann nicht nachgewiesen, ob wirklich eine Korrelation besteht.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Wenn ich zwei gleich große r habe. (z.B r= 7.18 und r= 7.18) und ein r davon signifikant ist. Wie kann ich dies begründen? Woran sehe ich, dass ein r von beiden signifikant ist und die andere nicht? Obwohl beide gleich groß sind?
Hallo Meli,
dann sind die verwendeten Stichproben wohl unterschiedlich groß? Um welche verwendete Methode geht es bei Dir?
Schöne Grüße
Daniela
Hallo Daniela
Ich möchte die Korrelation meiner Daten gerne auch innerhalb der Gruppen sehen. Also konkret, ist die Korrelation zweier Tests in der Interventionsgruppe grösser oder kleiner als jener der Kontrollgruppe. Gibt es im SPSS eine Möglichkeit, die Korrelation zwischen zwei Variablen nach Gruppen durchzuführen?
Tausend Dank für deine Mühe!
Liebe Grüsse Mirjam
Hallo Mirjam,
grundsätzlich kannst Du die Korrelationen auf den Untergruppen rechnen, entweder, indem Du jeweils über „Fälle auswählen“ Dir vor der Rechnung die entsprechende Gruppe definierst. Oder Du teilst die Datei vor der Rechnung der Korrelation auf (Daten -> aufgeteilte Datei), das geht noch schneller. Dann bekommst Du die Korrelation pro Gruppe. Interessant ist dann noch, ob sie sich auch signifikant unterscheiden (die Korrelationskoeffizienten), das geht nicht direkt in SPSS, lässt sich aber leicht von Hand nachrechnen, siehe Blogbeitrag https://statistik-und-beratung.de/2013/06/korrelationen-vergleichen/
Schöne Grüße
Daniela
Hallo Frau Keller!
Im Rahmen einer Studienarbeit will ich untersuchen, inwieweit die Kulturdimension „Machtdistanz“ nach Hofstede mit der Korruptionsanfälligkeit der betrachteten Länder korreliert. Für beide Faktoren gibt es sog. Indizes, der sowohl bei dem Index für Machtdistanz, als auch bei dem Index für Korruptionsanfälligkeit von 0-100 reicht. Während bei dem Machtdistanzindex der Wert 0 für keine und 100 für eine hohe Machtdistanz steht, verhält es sich bei dem Korruptionsindex genau umgekehrt. 0 steht hier für eine hohe und 100 für keine Korruptionsanfälligkeit. Will ich jetzt einen aussagekräftigen Korrelationswert ermitteln, müsste ich die Werte bei einem der beiden Indizes „umcodieren“, oder?
Vielen Dank und viele Grüsse
Hallo Tom,
nein, Du kannst sie auch so belassen, musst nur bei der Interpretation des Korrelationskoeffizienten dann die Richtung im Hinterkopf haben.
Schöne Grüße
Daniela