Konfidenzintervalle bezeichnen – wie der Name schon sagt – Intervalle mit ein Ober- und einer Untergrenze. Sie geben die Sicherheit der Schätzung einer gesuchten Kenngröße, z.B. des Mittelwerts, an. Das gängigste Konfidenzintervall ist das 95 %-Konfidenzintervall.
Wie groß sind Frauen?
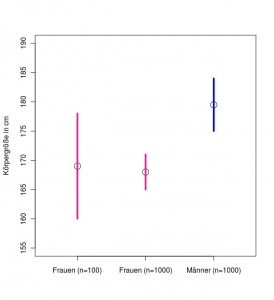
Ein Beispiel: wir sammeln Daten über die Körpergröße von 100 Frauen, um herauszufinden, wie groß Frauen sind. Dazu können wir den Mittelwert berechnen und erhalten 169cm. Wenn wir nun zusätzlich das 95 %-Konfidenzintervall für diesen Mittelwert angeben, können wir gut einschätzen, wie wir diesem Wert vertrauen können. Konfidenzintervalle werden auch Vertrauensbereiche genannt. Sagen wir, die Untergrenze des 95 %-Konfidenzintervalls liegt bei 160cm und die Obergrenze bei 178cm. Dann ist die Wahrscheinlichkeit dafür, dass bei der Ziehung einer weiteren Stichprobe (vom gleichen Umfang und aus der gleichen Grundgesamtheit) der neu ermittelte Mittelwert zwischen 1,60m und 1,78m liegt, mindestens 95 %.
Mehr Daten
Sammeln wir noch weitere Daten, so dass insgesamt Messungen von 1000 Frauen vorliegen, so wird sich der Mittelwert vermutlich wenig von der ersten Berechnung unterscheiden. Allerdings wird das Konfidenzintervall kleiner. Die Grenzen nähern sich an den Mittelwert an, da mit einer größeren Stichprobe die Sicherheit der Mittelwertsschätzung zunimmt. Nun haben wir den Mittelwert 168cm und das 95 %-Konfidenzintervall zwischen 165cm und 171cm.
Gruppenvergleich
Konfidenzintervalle können auch verwendet werden, um zwei Gruppen auf Unterschiede zu untersuchen. Angenommen, das 95 %-Konfidenzintervall der mittleren Körpergröße von 1000 Männern habe die Grenzen 175cm und 184cm. Da sich dieses Konfidenzintervall nicht mit dem der 1000 Frauen von oben überlappt, kann man hier auf einen signifikanten Unterschied zwischen der Körpergröße von Männern und Frauen schließen . Verwendet man das kleinere 100er Sample der Frauen, so reichen die Daten für diesen Nachweis nicht aus: die beiden Intervalle überlappen sich.
Unterschied der Mittelwerte
Eine andere Möglichkeit zum Gruppenvergleich ist die Verwendung des Konfidenzintervalls für den Unterschied der Mittelwerte. Hier wird nur ein Intervall berechnet, und zwar das Konfidenzintervall der Differenz der Mittelwerte. Wenn dieses die Null nicht einschließt, gibt es einen signifikanten Unterschied zwischen den beiden Gruppen (Signifikanzniveau 5% bei Verwendung des 95 %-Konfidenzintervalls).
Konfidenzintervalle sind eine gute Möglichkeit, um die Güte eines Schätzers anschaulich zu machen und interpretieren zu können. Zudem kann eine direkte Verbindung zwischen dem Konfidenzintervall und dem p-Wert beispielsweise eines t-Tests hergestellt werden.
Die hier verwendeten Zahlen sind als Beispiele gedacht und frei erfunden. Sie basieren nicht auf tatsächlichen Erhebungen.

Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.





Hallo Daniela,
heißt das, wenn der p-Wert größer als 0,05 ist, dass beide Therapien gleich gut wirken?
Ist der p-Wert größer als 0,05, wenn das 95%-Konfidenzintervall für die Risikodifferenz zweier Behandlungen die 0 enthält?
Beste Grüße
Charlotte
Hallo Charlotte,
zur Frage 1: nein, das heißt nur, dass man nicht nachweisen kann, dass sie unterschiedlich wirken.
zur Frage 2: Das kommt auf den Test an, der berechnet wurde, aber annähernd: ja.
Schöne Grüße
Daniela
Hallo Daniela,
auch ich habe eine Frage bezüglich des Konfidenzintervalls.
Ich stehe gerade vor der Herausforderung den Konfidenzbereich festzulegen. Die Angabe lautet:
Ermitteln sie den Konfidenzbereich eines Mittelwertes von 3 bei einem Konfidenzintervall von 1,5.
Ich bin mir nicht sicher ob dieser dann 1,5 (untere Grenze) und 4,5 (obere Grenze) oder 2,25 (untere Grenze) und 3,75 (obere Grenze) betragen soll.
Vielen Dank für deine Hilfe
Hallo Robert,
da bin ich mir auch nicht sicher. Genauer wäre es, wenn dort stünde „Konfidenzintervall der Breite 1,5“.
Weitere Fragen gern in der Facebookgruppe Statistikfragen posten: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Hallo Daniela,
erst mal super Erklärung. Aber ich habe dennoch eine Frage. Ich weiß wie ich das alles berechnen muss (meine Werte: Kontingenztafel: a = 38, b = 18; c = 16, d = 211, insgesamt 283 Proben) und bekomme eine OR von 27,8 mit einem 95%-KI von 13,06-59,34. Ebenso eine RR von 8,95 mit einem 95%-KI von 5,56-14,41.
Sehe ich das richtig, dass sowohl OR, als auch RR signifikant sind, da sie im KI liegen? Aber ist eine KI von ca. 46, bze. 9 nicht viel zu groß? Wie groß sollte der KI-Intervall mindestens, bzw. höchstens sein um eine gute Aussage treffen zu können?
Kann ich agumentieren, dass die Werte zwar signifikant sind, aber das KI-Intervall so groß ist, dass eine größe Stichprobe gezogen werden muss, um eine definitive Aussage treffen zu können?
Ich hoffe ich habe das verständlich beschrieben.
Vielen Dank im Voraus
Stefanie
Hallo Stefanie,
du siehst, dass die beiden Werte signifikant sind, da die 1 nicht im Intervall liegt. Eine OR von 1 würde beudeuten „kein Zusammenhang“. Da die 1 nicht eingeschlossen ist, hast du eine signifikante OR. Das ist ein sehr deutliches Ergebnis, da die Werte so hoch sind. Du brauchst keine größere Stichprobe.
Schöne Grüße
Daniela
Vielen Dank für deine schnelle Antwort. Ein schönes Wochenende
Hallo Daniela,
Erstmal: toller Block und er hat mir auch echt geholfen das ganze zu verstehen. Nun bin ich jedoch mitten in meiner Bachelorarbeit und es ist ein weiteres Problem aufgetreten. Ich habe einen Excel- File bekommen indem ich mich einarbeiten soll. Hier wurde nun der 95% Cl ermittelt durch folgende Formel:
=KONFIDENZ(0,05; bestimmte SD; bestimmtes N)
Dort bekomme ich nun einen bestimmten Wert (hier:0,026) heraus. Die Mittelwerte die vorher erhoben wurden lagen jedoch alle über 0,09. Ich steh nun leider mächtig auf dem Schlauch was mir dieser eine Wert(0,026) sagen soll.
Ich hoffe du kannst mir da weiter helfen. Vielen Dank schonmal
Beste Grüße
Jessy
Hallo Jessy,
der Wert ist die Hälfte des Konfidenzintervalls. Den addierst du zum Mittelwert dazu, um die Obergrenze des Intervalls zu bekommen. Dann subtrahierst du ihn vom Mittelwert, um die Untergrenze zu bekommen. Siehe auch hier: https://support.office.com/de-de/article/KONFIDENZ-Funktion–75ccc007-f77c-4343-bc14-673642091ad6
Schöne Grüße
Daniela
Mich würde interessieren was das Konfidenzintervall für die Steigung einer Regressionsgeraden aussagt. Das peil ich noch nicht.
Hallo Jonathan,
das Konfidenzintervall für die Steigung gibt dir einen „Sicherheitsbereich“ für die Steigung an. Damit sagt es dir also in welchem Bereich der Wert mit einer bestimmten Wahrscheinlichkeit (z.B. 95 %) liegen würde, wenn man ihn an einer neuen Stichprobe nochmals ausrechnen würde. Du siehst damit also, wie sicher deine Schätzung der Steigung ist. Dabei ist die Untergrenze die kleinste Steigung (flache Gerade), die Obergrenze die größte Steigung (steile Gerade).
Reicht die Erklärung?
Schöne Grüße
Daniela
Hi Daniela,
ich stehe vor einer ähnlichen Frage: Ich untersuche den Zusammenhang von zwei unterschiedlichen Messungen (á 1000 Datenpunkten). Die Messungen können durch eine lineare Regression sehr gut beschrieben werden (r=0,98). In MATLAB kann ich mir dabei die CI bzw. die PI dazu plotten und berechnen, was ich beides nachvollziehen kann. Allerdings habe ich Schwierigkeiten mit der Interpretation. Was genau sagt mir jetzt das Konfidenzintervall?
Viele liebe Grüße,
Johnny
Hallo Johnny,
ist das das Konfindenzintervall für r, das du da bekommst? Oder für den Regressionskoeffizienten? Gib doch mal hier die Zahlen, damit wir das am Beispiel besprechen können.
Schöne Grüße
Daniela
Sehr geehrte Frau Keller,
in ihrem Artikel schreiben Sie: „Konfidenzintervalle sind Teil der deskriptiven Statistik“. In allen meinen Büchern werden die Konfidenzintervalle jedoch in den Bereich der induktiven Statistik eingeordnet.
Hallo Eric,
ja, da haben Sie recht. Ich habe es geändert.
Schöne Grüße
Daniela Keller
Hallo ich habe ein Frage bezüglich der Konfidenzintervalle. Ich habe eine Variable A mit einem Mittelwert und einem Konfidenzintervall. Ich möchte Var A und B vergleichen in einem jeweiligen Zeitstrahl und will nachsehen ob sich die Konfidenzintervalle überschneiden. Da dies der Standardfehler des MW ist addiere/subtrahiere ich die Hälfte des Konfidenzintervalls zum jeweiligen Mittelwert und habe somit mein Intervall. Wenn sich die Intervalle überschneiden kann keine Aussage darüber getroffen werden, was als besser/schlechter klassifiziert werden kann. Die Frage ist ob ich zb Konfidenzintervall von Var A von 2 also dem MW +/- 1 hinzufügen kann? Vielen Dank für die Hilfe, bin schon am verzweifeln…
Hallo Mark,
die Frage verstehe ich nicht, sorry! Kannst du sie bitte nochmal anders formulieren?
Gruß
Daniela
Hallo,
eine Anmerkung zu der Aussage, dass sich die KI nicht überlappen dürfen um stat. Signifikanz zu implizieren. Dies ist meiner Meinung nach nicht korrekt. Es ist hinreichend für die stat. Signifikanz wenn die KI nicht überlappen, aber nicht der Umkehrschluss. So können die KIs überlappen und trotzdem die Differenz der Werte signifkant sein.
Vielmehr gilt, dass wenn das KI der Differenz zweier Schätzungen nicht 0 umfasst, stat. Signifikanz vorliegt.
Beste Grüße
Ja, das stimmt.
Hallo Daniela,
ich unterrichte auch Statistik. Am liebsten würde ich die Hypothesentests weglassen und die Signifikanz nur über Konfidenzintervalle abhandeln. Diese geben schließlich noch zusätzliche Information über Richtung und Stärke von Effekten. Wegen des „Lehrplans“ muss ich aber beide Herangehensweisen behandeln. Nun hatte ich aber auch schon öfter den Fall, dass sich zwei Konfidenzintervalle überlappen, der t-Test aber p-Werte kleiner als 0,05 ergeben haben und Minitab ein KI der Differenz ausgegeben hat welches die Null nicht enthält. Das finden ich und die Schulungsteilnehmer sehr befremdlich. Liegt das möglicherweise an der unterschiedlichen berechnung der Freiheitsgrade beim t-Test gegenüber der Situation bei Konfidenzintervallen?
Liebe Grüße,
Till
Hallo Till,
hm, darauf weiß ich auch keine Antwort. Ich weiß nicht, ob das an der unterschiedlichen Anzahl der Freiheitsgrade liegt. Das müsste man sich mal an einem Beispiel von Hand nachrechnen. Hast Du das mal gemacht?
Schöne Grüße
Daniela
Hallo Daniela,
von Hand komme ich nur beim 1-Stichproben-t- oder Gauß-Test auf stimmige Ergebnisse. Unterschiede tauchen nur bei 2-Stichprobentests auf. Einiges an Nachdenken und googlen führt mich in die Richtung, dass dei 2-Stichprobentests nicht die individuellen KI der Mittelwerte relevant sind sondern das der gemeinsamen Differenz, und hier entsteht der Unterschied dadurch, dass die gemeinsame Standardabweichung anders berechnet wird als die einzelnen. Fazit: Die Überlappung eines einzelnen KI mit einem festen Wert (1-Stichprobentest) gibt das gleiche Ergebnis wie der betreffende Hypotest. Bei 2-Stichproben gegeneinander muss man schauen ob das KI der Differenz (der Mittelwerte) die 0 enthält und bekommt eine mitunter Abweichende Aussage als bei der Betrachtung ob die individuellen KI der Stichprobenmittelwerte überlappen oder nicht…
LG,
Till
Hallo Till,
ja, das ist richtig.
Schöne Grüße
Daniela
Hallo Daniela,
momentan ist Statistik eines meiner Fächer während des Studiums und heute wurde mir folgende Aufgabe gegeben, an der ich mir den Kopf zerbreche:
Bestimme das 95% Konfidenzintervall für den Unterschied des Prozentsatzes „Very early adopters“ unter Männern und unter Frauen.
Gegeben dazu ist folgende Tabelle:
I Not early adopter I Medium early adopter I Very early adopter
Männer I 19 I 20 I 6
Frauen I 24 I 33 I 10
Wie muss ich hier vorgehen?
Danke im Vorraus
Thorben
Hallo Thorben, hier berechnest du das Konfidenzintervall für den Unterschied der beiden Anteile 6/45 (Männer) und 10/67 (Frauen).Eine Anleitung dazu findest du hier: http://startistik.csd.univie.ac.at/inferenz/details.jsp unter Abschnitt „Beispiel zur Differenz von Anteilswerten“.
Schöne Grüße
Daniela
Hallo Daniela,
ich habe ansich die ganze Sache verstanden. Nun habe ich das Problem, dass über die KI-Grenzen keine Signifikanz zwischen zwei Tests aufgezeigt wird. Berechne ich die Signifikanz über den t-Test stellt dieser eine Signifikanz fest. Welche Methode ist denn die „sicherere“ um signifkanzen aufzuzeigen?
Viele Grüße
Marie
Hallo Marie,
„sicherer“ eigentlich nicht, aber praktischer ist der t-Test. Wahrscheinlich sind aber beide Ergebnisse knapp, oder?
Schöne Grüße
Daniela
Hi :o) ich bin ein absoluter Laie in der Statistik, muss jedoch meine Bachelorarbeit damit ein wenig aufwerten. Wie kann es sein, dass SPSS mir Signifikanzgruppen anzeigt, die in Excel mit FehlerbalkenGraphiken nicht wiederzugeben sind?! Für die Fehlerbalken gebe ich den SE an, jedoch überlappen sich die (lt. SPSS) zugehörigen Balken/Gruppen nicht. 🙁
Hallo,
das kann ich leider so auch nicht beantworten. Was meinen Sie mit „Signifikanzgruppen“? Welche Werte genau nehmen Sie für die Fehlerbalken? Wenn Sie mit Fehlerbalken darstellen wollen, ob es einen signifikanten Unterschied gibt, sollten Sie nicht nur die SE als Balken nehmen, sondern die 95 % Konfidenzintervalle als Fehlerbalken darstellen (die Sie aus den SE berechnen können).
Schöne Grüße
Daniela Keller
Hi 🙂 danke für die schnelle Antwort.
Mit den Signifikanzgruppen meine ich die „Untergruppen“, die SPSS mir aus dem Tukey-Test zeigt. Diese zeigen mir doch signifikante Unterschiede zwischen den Varianten, oder?
Auch, wenn ich den Kovidenzintervall in den Fehlerbalken angebe, überschneiden sich die Balken nicht.
Vielleicht liegt der Fehler aber auch bei meiner Interpretation der SPSS-Daten?! :-/
Der Tukey Test überprüft alle paarweisen Vergleiche. Für jeden Vergleich gibt er einen p-Wert (Spalte „Sig.“) aus. Ist der kleiner als 0,05, so ist dieser Paarvergleich signifikant.
Schöne Grüße
Daniela Keller
Hallo Daniela!
Schöne Seite und toller Blog!
Vielleicht kannst du mir bei meiner Frage auch weiterhelfen:
Wie wenn ich in einer Stichprobe zwei Variablen habe (Kosten_1 und Kosten_2) und für beide Variablen den Median habe:
n=150 Median: Kosten_1 = 120€
n=150 Median: Kosten_2 = 150€
Wie kann ich dann prüfen ob sich die Mediane signifikant unterscheiden?
Ist das schwer?
Ich habe hier SPSS und Excel.
Viele Grüße und einen schönen Abend noch
Hallo Thomas,
da bietet sich der Wilcoxon-Test an. Er vergleicht nicht direkt die Mediane, sondern arbeitet mit den Rängen der Daten, passt aber von der dahinter stehenden Idee gut zu den Medianen. Deshalb verwendet man auch zusätzlich zu diesem Test oft die Mediane zur Beschreibung des Unterschieds. Er ist für alle metrischen Variablen geeignet, egal ob normalverteilt oder nicht. Er vergleicht die Lage von zwei Messwiederholungen (Kosten1 und Kosten2), indem deren Ränge verglichen werden.
In SPSS brauchen Sie dafür zwei Spalten, eine mit den Daten zu Kosten1, eine zu Kosten2, jeweils 150 Zeilen. Den Test finden Sie über Analysieren -> nichtparametrische Tests -> alte Dialogfelder -> 2 verbundene Stichproben. Dort die beiden Variablen eingeben. Wenn der p-Wert („Sig.“) kleiner als 0,05 ist, gibt es einen signifikanten Unterschied. Wenn nicht, kann der Unterschied nicht als signifikant nachgewiesen werden.
Schöne Grüße
Daniela Keller
Hi Daniela
Ich bin gerade hier gelandet, weil ich im Netz nach „Konfidenzintervallen“ und „Signifikanz“ gesucht habe. Vielleicht kannst du mir ja bei meinem Problem bzw. meiner Frage weiterhelfen. Eigentlich ist ein „ja“ oder „nein“ fast ausreichend. *g*
Ich werte gerade einen Datensatz aus der Daten zur folgenden Frage enthält: „Mit welchem Verkehrsmittel kommen Sie zur Arbeit?“ Zur Auswahl standen „Pkw“, Öpnv“, „Rad“, „Sonstiges“. Jetzt würde ich gerne wissen, ob sich die einzelnen Angaben signifikant voneinander unterscheiden und ob sich sich die (Prozent)Angaben bei drei Altersklassen signifikant unterscheiden.
Bin ich da richtig informiert, dass das mit dem Wilson-Score-Intervall möglich ist?
Also die Konfidenzintervalle einmal paarweise für PKW & ÖPNV, PKW & Rad usw. und einmal paarweise für PKW & Altersklasse 1, PKW & Altersklasse 2 und prüfen, ob es da Überlappungen gibt? Bei Überlappungen sind die Unterschiede nicht signifikant, ohne Überlappungen sind die Unterschiede signifikant?
Ich verwende hierzu den folgenden Konfidenzintervallrechner: http://www.pedro.org.au/wp-content/uploads/CIcalculator.xls
Mache ich das so richtig oder stimmt das nicht?
Viele Grüße und einen schönen Sonntag
samy
Hallo Samy,
ich kenne zwar den Konfidenzintervallrechner nicht, aber die Methode und die Umsetzung ist die richtige. Also „Ja“. 🙂
Schöne Grüße
Daniela Keller
Hallo Daniela,
zunächst einmal vielen Dank für Deine tolle Erklärung. Sie hilft mir bei meinen Vorbereitungen auf die Klausur im Fach Wissenschaftliche Methodik sehr weiter.
Ich habe noch eine Frage zur Berechnung des Konfidentintervalls. In der Formel gibt es ein u1-alpha/2. Das ist scheinbar ein Quantil aber ich verstehe nicht wo ich den Wert dafür her bekomme. Hat das etwas mit dem alpha-Niveau zu tun?
Im Voraus 1.000 Dank für eine kurze Rückmeldung
Hallo Julia,
das ist das Quantil der Normalverteilung, das entnimmt man z.B. aus Tabellen wie hier http://de.wikipedia.org/wiki/Tabelle_Standardnormalverteilung. Beim zweiseitigen 95 %-Konfidenzintervall ist es das 0,975-Quantil. (Alpha ist in dem Fall 0,05, davon die Hälfte -> 0,025. Das von 1 abziehen -> 0,975). In der Tabelle suchst Du den Eintrag, der möglichst nah an der 0,975 dran ist. In dem Fall sogar genau 0,97500. Dort gehst Du dann in dieser Zeile bis vor zur Zeilenbeschriftung (1,9*) und an der gleichen Stelle bis hoch zur Spaltenbeschriftung (6). Das baust Du zusammen (die 6 kommt an die Stelle des *) und bekommst 1,96. Das ist das 0,975-Quantil: 1,96.
Schöne Grüße
Daniela
Liebe Daniela,
vielen herzlichen Dank für die schnelle und vor allem sehr hilfreiche Rückmeldung. Nun habe ich es verstanden.
Sofern Du noch nicht an einer Universität oder Fachhochschule tätig bist, solltest Du Dich dort unbedingt bewerben. Es ist wirklich hervorragend, wie Du mit wenigen Worten verständlich erklärst, um was es geht. Solche Dozenten könnten wir gut gebrauchen.
Noch einmal vielen Dank!
Liebe Grüße Julia
Liebe Julia,
danke für die Blumen! 🙂 Ich freue mich, wenn Dir meine Erklärungen weiter helfen! Und ja, ich gebe auch Kurse an Hochschulen! 🙂
Schöne Grüße
Daniela
Guten Abend Daniela,
entschuldige die späte Meldung 🙂
Der Groschen ist gefallen. Dir ein herzliches Dankeschön für deine Mühen und viel Erfolg mit der statistischen Beratung!
Grüße
Andi
🙂 Danke und Dir ebenso viel Erfolg!
Schöne Grüße
Daniela
Hallo Daniela,
stark, so schnell eine Antwort – Danke! So ganz durchgedrungen ist es leider noch nicht. Ich habe heute wirklich den Tag damit verbracht, einige Artikel dazu zu lesen und den Versuch unternommen, das zu verstehen.
Bei einem anderen Autor finde ich den Hinweis „…the term ‚confidence‘ refers to the method and not to the result of the procedure…“ Es scheint (bei einem KI mit 95%) wohl so zu sein, dass bei 100 Untersuchungen unter exakt gleichen Bedingungen bei 95 der wahre Wert der Population im KI enthalten ist und bei 5 Fällen nicht.
Die Aussage bezieht sich sich nach meinem Verständnis auf die Methode und da gehört nicht nur die Stichprobe (Größe, Repräsentativität, etc.) dazu, sondern auch die verwendeten statistischen Verfahren (welchen Mittelwert bei kleinen Stichproben zur Zeitmessung, usw.), oder? Ich sage also aus, dass ich hinsichtlich der Methode sicher/zuversichtlich (confident) bin, dass der wahre Wert enthalten ist…
Was meinst du?
Grüße
Andi
Hallo Andi,
ein weiterer Erklärungsversuch: 🙂 Das Konfidenzintervall berechnet sich aus dem Standardfehler des Mittelwerts (und dem Mittelwert). Es ist also ein Sicherheitsbereich für den Mittelwert. Würde man viele weitere Stichproben der gleichen Größe aus der gleichen Grundgesamtheit ziehen, und daraus jeweils den Mittelwert berechnen, dann liegen davon 95 % der Mittelwerte in dem Konfidenzintervall, 5 % außerhalb.
Dabei wird aber davon ausgegangen, dass immer die gleiche Stichprobengröße, immer die gleiche Grundgesamtheit, und auch immer die gleiche Methode zugrunde liegt. Außerdem wird grundsätzlich beim Konfidenzintervall von Normalverteilung ausgegangen.
Natürlich hängt das Ergebnis (wie bei jedem statistischen Ergebnis) von der Grundgesamtheit, der Größe der Stichprobe, der Methode zur Ziehung der Stichprobe usw. ab. Das Konfidenzintervall muss also auch immer vor dem Hintergrund der Daten interpretiert werden.
Beantwortet das Deine Fragen?
Schöne Grüße
Daniela
Hallo zusammen,
ich bin gerade auf die Aussage gestoßen, dass Konfidenzintervalle keine Wahrscheinlichkeit ausdrücken.
Ich hoffe, dass ich hier auf die Website (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2947664/) dazu verlinken darf? Dort heißt es: „A confidence interval is not a probability, and therefore it is not technically correct to say the probability is 95% that…“ Und dieser Autor ist nicht der einzige, der diese Aussage tätigt.
Ich habe so den Eindruck, dass da keine Einigkeit herrscht, was es denn nun ist oder aussagt? Hier auf der Webseite (sofern ich das richtig verstehe) wird auch von einer Wahrscheinlichkeit gesprochen.
Würde mich über Klärung der Tatsachen freuen 🙂
Ciao
Andi
Hallo Andi,
ja, das Konfidenzintervall ist nicht der Bereich, in dem der „wahre“ Wert mit einer gewissen Wahrscheinlichkeit liegt, denn, wie in dem zitierten Artikel auch steht „Since the event (construction of the confidence interval) has already occurred, the true value of the targeted parameter either does or does not lie in the interval.“ Ich denke, es ist streng genommen der Bereich, in dem ein weiterer, noch nicht gemessener Wert (des gleichen Zielparameters) mit einer gewissen Wahrscheinlichkeit liegt.
Hilft das weiter? 🙂
Schöne Grüße
Daniela
Tut mir Leid, aber das ist völliger Schwachsinn. Betrachten wir alleine nur den Fall von KI für den Erwartungswert. Die Meinung des angegebenen Autors ist, dass 95% aller KI den wahren Erwartungswert einschließen. Das bedeutet: von allen aufgestellten KI liegt der wahre Erwartungswert in 95% von ihnen. Diese Aussage ist äquivalent dazu, dass der wahre Erwartungswert im MITTEL zu 95% in jedem einzelnen Intervall liegt. Eine andere Aussage steht in keinem mir bekannten Lehrbuch. (vgl. u.a. Fahrmeier: Statistik)
Hallo Leute.
Eine Frage zum CI. Dürfen sich die SD (Standartabweichungen) zwischen 2 Gruppen (A,B) nicht überlappen um einen signifikanten Unterschied zu gewährleisten oder reicht es wenn sich ein Mittelwert (Gruppe A) nicht mit dem Streuungsmaß überlappt?
Danke für eure Hilfe
Hallo Christian,
die Grenzen der Konfidenzintervalle dürfen sich nicht überlappen. Also, die untere Grenze des CIs zum größeren Mittelwert muss größer sein als die obere Grenze des CIs zum kleineren Mittelwert. Dass die Grenzen nicht mit dem anderen Mittelwert überlappen reicht nicht aus. Aber Achtung: die Grenzen des CIs sind NICHT die Standardabweichungen!
Viele Grüße
Daniela
Prima, endlich mal jemand der es mit einem banalen Beispiel versucht zu erklären! Vielen Dank, es ist sehr verständlich geschrieben!