Schiefe (Skew) und Exzess (Kurtosis) sind Maße, die die Abweichung einer Verteilung von der Normalverteilung beschreiben.
Schiefe
Die Schiefe gibt dabei an, ob die Verteilung symmetrisch ist oder nicht.
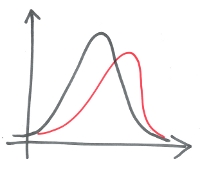
Eine positive Schiefe beschreibt dabei rechtsschiefe Daten (links steil, rechts schief). Hier gibt es viele kleine Werte in den Daten.
Eine negative Schiefe beschreibt linksschiefe Daten (links schief, rechts steil). Hier kommen viele große Werte vor und weniger kleine Werte.
Linkssteile, rechtsschiefe Verteilung
Exzess (Kurtosis)
Der Exzess gibt dagegen die Wölbung an und beschreibt, ob die Verteilung im Gegensatz zur Normalverteilung spitz oder abgeflacht ist.
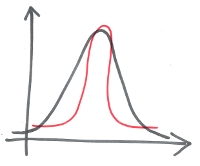
Eine spitze Verteilung hat einen positiven Exzess. Hier liegen dann mehr Beobachtungen als gewöhnlich in den Enden der Verteilung, weshalb diese auch heavy-tailed genannt wird.
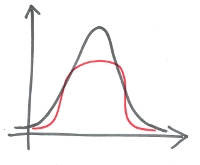
Ein negativer Exzess beschreibt eine abgeflachte Verteilung. Eine solche Verteilung hat im Vergleich zur Normalverteilung dünne Enden (light-tailed).
Spitze Verteilung mit dicken Enden
Flache Verteilung mit dünnen Enden
Du willst mehr Durchblick im Statistik-Dschungel?
Was ist normal?
Bei normalverteilten Werten sind sowohl Exzess als auch Schiefe gleich 0. Je weiter die Werte von der Null entfernt sind, umso weniger wahrscheinlich sind die Daten nicht normalverteilt.
Folgendermaßen kannst du prüfen, ob der Wert (Exzess oder Schiefe) signifikant von der 0 abweicht und somit signifikant keine Normalverteilung vorliegt:
Teile den Wert durch seinen Standardfehler, nimm den Betrag des Ergebnisses. Ist dieses Ergebnis größer als 1.96, so liegt eine signifikante Schiefe bzw. ein signifikanter Exzess vor (zum Signifikanzniveau von 5 %).
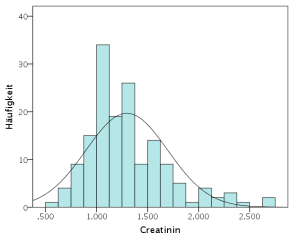
Im Beispiel hier liegt eine Schiefe von 1.209 vor mit einem Standardfehler von .193. Der Quotient aus beiden ergibt also 1.209/.193 = 6.26 und damit einen Wert über der Grenze 1.96. Die Verteilung hat also eine positive Schiefe (links steil, rechts schief), die signifikant von der 0 abweicht.
Für den Exzess (= Kurtosis) ergibt sich der Quotient 1.754/.384 = 4.57. Auch hier liegt also eine signifikante positive Abweichung von der 0 vor (spitz, mit dicken Enden).
Das Histogramm zu diesem Beispiel mit Normalverteilungskurve sieht so aus:
Solche Prüfungen auf signifikante Abweichungen sollten aber mit Vorsicht verwendet werden. Bei großen Stichproben werden auch kleine Abweichungen als signifikant erkannt. In diesen Fällen also lieber die grafische Einschätzung der Normalverteilung – einen Q-Q-Plot – verwenden.

Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.







Hallo, erstmal vielen Dank für die Erklärung, sehr hilfreich! Das Vorgehen über die z-transformierte Schiefe und Kurtosis und die Grenzwerte von 1,96 waren mir bisher nicht bekannt. Könnten Sie vielleicht eine Quelle angeben, wo man das mal etwas detaillierter nachschlagen könnte? Vielen Dank!
Hallo Michelle,
das steht z.B. in Andy Field, Discovering Statistics Using SPSS, 4. Auflage, 2013, Sage, S. 184.
LG Daniela
P.S.: Willst Du mehr Input und Hilfe in Deiner Statistik? Dann komm in die Statistik-Akademie: https://statistik-und-beratung.de/mitgliederbereich-lp/
Wie interpretiere ich meinen Wert, wenn dieser 0,200 ist?
Liebe Grüße Marlene
Hallo Marlene,
welcher Wert ist 0,2?
LG Daniela
Hallo,
falls meine Variablen jetzt nicht normalverteilt sind bedeutet dies, dass ich sie nicht für meine Analyse verwenden kann?
Wie ist das weitere Vorgehen bei Variablen die nicht normalverteilt sind?
Danke! Eva
Hallo Eva,
dann verwendest Du nicht-parametrische Methoden. Welche genau hängt davon ab, was genau Du untersuchst. Sieh Dir dazu doch mein kostenloses E-Book oder meinen Gratis E-Mail-Kurs zur Methodenauswahl an. Findest Du beides oben im Menü unter „Free“.
LG Daniela
Hallo,
angenommen, ich möchte die Schiefe und Wölbung der Verteilungen zweier unterschiedlicher Parameter miteinander vergleichen. Gibt es stat. Test, der dieses kann bzw. zu der Aussage führt, die Schiefe der Veteilungen sind signifikant verschieden?
Hallo,
einen Test dafür kenne ich nicht. Aber Du kannst Dir die Werte mit Konfidenzintervall berechnen lassen (in SPSS z.B. bekommst Du die Standardfehler zu den Werten dazu und kannst Dir daraus selbst die Konfidenzintervalle erstellen) und dann die Intervalle vergleichen. Überschneiden sie sich nicht, so gibt es einen signifikanten Unterschied.
Schöne Grüße
Daniela
Hallo. Danle für die schnelle Rückmeldung, das werde ich ausprobieren. Ich hatte Verteilungen von Temperaturen miteinander verglichen. Eine Kurve ist deutlich stärker gewölbt (spitzer) als die andere (Kurtosis 3.2 zu 0.7), der Mittelwert aber nahezu identisch. Genau um die Quatifikation / Signifkanz der Unterschiede in dieser Form geht es. Könnte man eventuell die Dichteveteilungen darauf testen, ob sie aus der gleichen Grundgesamtheit stammen? Viele Grüße Mirco
Hallo Mirco,
Du kannst Verteilungen auf Gleichheit testen, ja. Sieh Dir dazu z.B. den Chi-Quadrat-Test an.
LG Daniela
Hallo. Danke für die schnelle Rückmeldung, das werde ich ausprobieren. Ich hatte Verteilungen von Temperaturen verglichen die sich stark in der Kurtosis unterschieden (3.2 zu 0.7), die aber um den gleichen Mittelwert schwankten. Gerade diese Form-Änderung ist der interessierende Aspekt. Gruß Mirco
Hallo Frau Keller,
Kompliment zu dem verständlichen Beitrag erstmal. Wie interpretiere ich meine Verteilung wenn der Wert für die Schiefe 1.96 ist? Vielen Dank!
Hallo,
positive Schiefe bedeutet, dass die Daten rechtsschief sind. Ob das eine signifikante Abweichung von der Normalverteilung ist lässt sich allein aus der Schiefe heraus nicht sagen, dazu braucht man noch die Fallzahl. Testen kann man das mit z.B. Kolmogorov-Smirnoff-Test oder Shapiro-Wilk-Test.
Schöne Grüße
Daniela