Bootstrapping ist eine Resampling-Methode, die Du einsetzen kannst, um z.B. nicht erfüllte Voraussetzungen wie Normalverteilung Deiner Daten zu umgehen.

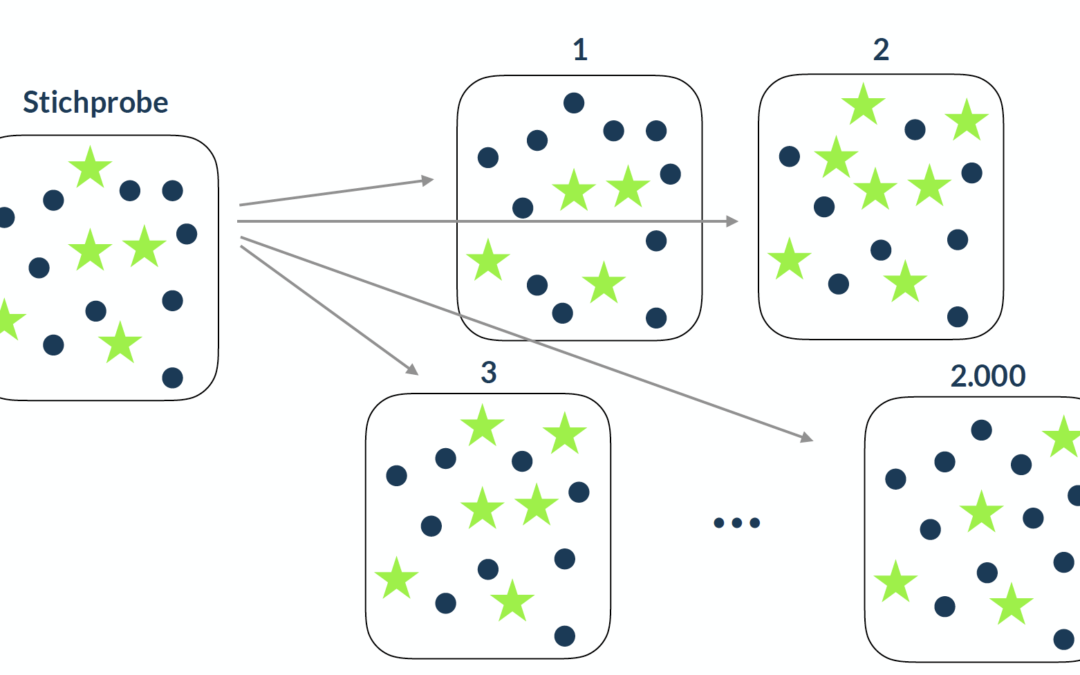
Beim Bootstrapping werden aus Deiner Stichprobe sehr viele Stichproben (z.B. 2.000) mit Zurücklegen gezogen. Auf diesen vielen Stichproben wird die Datenanalyse dann jeweils durchgeführt. Diese vielen Ergebnisse werden anschließend zu einem Gesamtergebnis zusammengefasst und oft mit Konfidenzintervall angegeben. Dieses Gesamtergebnis ist dann verlässlich, selbst wenn z.B. keine Normalverteilung vorliegt oder Ausreißer in den Daten sind.

Wozu brauche ich Bootstrapping?

Du kannst Bootstrapping einsetzen, um

• parametrische Methoden zu verwenden, selbst wenn die Voraussetzungen dafür nicht erfüllt sind.
• die Voraussetzungen wie Normalverteilung, Varianzhomogenität, keine Ausreißer und Linearität zu umgehen.
• Konfidenzintervalle für Schätzwerte (z.B. für den Median) zu berechnen.

Wann kann ich Bootstrapping nutzen?

Du kannst Bootstrapping für fast jede statistische Analyse nutzen. Voraussetzung ist, dass Deine Software Bootstrapping implementiert hat und dass Du genügend Rechenpower hast. Die meisten Statistikpakete, z.B. auch SPSS und R, haben Bootstrapping im Funktionsumfang. Die Rechenpower ist bei modernen Computern kein Problem mehr. Außerdem darf Deine Stichprobe nicht zu klein sein. Denn es werden ja aus Deiner Stichprobe sehr viele neue Stichproben gezogen. Es gibt verschiedene Empfehlungen für die Mindestanzahl, um mit Bootstrapping arbeiten zu können. Chernick (2008) empfiehlt mindestens N = 50. Kabakoff (2015) meint mindestens 20 bis 30.

Wie verwende ich Bootstrapping mit SPSS oder R?

Wenn Deine Software Bootstrapping implementiert hast, kannst Du meist direkt zu Deiner gewünschten Datenanalyse das Bootstrapping zusätzlich rechnen.

In SPSS ist immer dann, wenn Bootstrapping möglich ist, ein Button „Bootstrap“ vorhanden. Auf den klickst Du und nimmt dort die nötigen Einstellungen vor. Ist kein Bootstrapping möglich, z.B. weil Du auf deinem multiple-imputierten Datensatz arbeitest oder weil Du eine schrittweise Regressionsanalyse ausgewählt hast, dann ist dieser Button ausgegraut und nicht klickbar. Die nötigen Einstellungen sind:

• die Auswahl der Anzahl der Stichproben (z.B. 2000),
• die Einstellung von Seed (wenn die Analyse reproduzierbar sein soll) und
• die Auswahl der Methode zur Berechnung des Konfidenzintervalls (Percentile oder Bias-corrected).

In R nutzt Du die Funktion boot() aus dem Paket „boot“. Hier sind drei Schritte nötig:

1. Du erstellst die Funktion, die die gewünschte Statistik berechnet.
2. Du führst das Bootstrapping durch.
3. Du berechnest die Konfidenzintervalle aus dem Bootstrapping.

Auch hier gilt wie bei SPSS oben, dass Du die Anzahl der Stichproben, den Seed und auch die Methode zur Berechnung des Konfidenzintervalls vorgibst.

 Referenzen:

• Robert I Kabacoff (2015) R in Action. Data analysis and graphics with R. 2. Auflage, Manning Publications Co, NY.
• Michael R. Chernick (2008) Bootstrap methods: a guide for practioners and researchers, 2. Auflage, Hoboken, NJ: Wiley.