Wozu Effektstärkemaße?
Maße für die Effektstärke geben dir die Größe und die Richtung eines Unterschieds bzw. eines Zusammenhangs an. Damit sind sie essentiell zur Interpretation der Ergebnisse einer statistischen Analyse.
Meist werden standardisierte Effektstärkemaße verwendet, die unabhängig von der Maßeinheit der Skala interpretiert werden. Das hat zwei Vorteile:
- Erstens kann der Effekt auch bei nicht sinnvoll interpretierbarer Einheit quantifiziert werden. Beispielsweise ist ein Punktunterschied von 2.5 auf einer Angst-Skala schwierig zu interpretieren. Für das standardisierte Maß wird der Unterschied durch die Standardabweichugn geteilt und kann somit in der Einheit „Standardabweichungen“ interpretiert: „Der Mittelwert der Testgruppe lag 1.5 Standardabweichungen höher als der der Kontrollgruppe.“
- Zweitens sind die Ergebnisse über verschiedene Studien hinweg vergleichbar und es existieren Interpretationshilfen, die z.B. einen „kleinen“, „mittleren“ oder „starken“ Effekt unterscheiden.
Welche Effektstärkemaße?
Im Folgenden gebe ich dir eine Übersicht über die wichtigsten Effektstärkemaße, ihre Berechnung und Interpretation.
Unterschied zwischen zwei Mittelwerten: Cohens d
Cohens d wird als Effektstärkemaß für den Vergleich von zwei Mittelwerten verwenden, passt also zum t-Test. Berechnet wird d aus der Differenz der beiden Mittelwert geteilt durch die Standardabweichung der Kontrollgruppe.
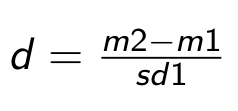
Unterschied zwischen zwei Medianen: r
Für den Unterschied zwischen zwei Medianen (also passend zum Mann-Whitney U Test bzw. Wilcoxon Test) wird aus der standardisierten Teststatistik des entsprechenden Tests (z) und der Fallzahl (N) die Effektgröße r berechnet.
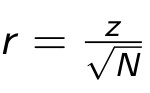
Du willst mehr Durchblick im Statistik-Dschungel?
Unterschied zwischen mehr als zwei Mittelwerten: Eta-quadrat
Für den Unterschied zwischen mehr als zwei Mittelwerten wird die ANOVA berechnet und hierzu passt als Effektstärkemaß Eta-quadrat. Es wird aus den Fehlerquadratsummen berechnet.
In SPSS kannst du in den Optionen angeben, dass du den Wert ausgegeben haben möchtest. Dort wird er als „partielles Eta-quadrat“ bezeichnet, in der einfaktoriellen ANOVA ist das aber genau der Eta-quadrat-Wert, den wir hier brauchen.
Zur Interpretation werden folgende Grenzen genutzt: kleiner als 0.06 zeigt einen kleinen Effekt, zwischen 0.06 und 0.14 steht für einen mittleren Effekt und größere Werte bezeichnen einen starken Effekt.
Unterschied zwischen mehr als zwei Medianen
Für den Vergleich von mehr als zwei Medianen (als Test wäre das Kruskal-Wallis) gibt es keine einfache Berechnung eines Effektstärkemaß, deshalb wird empfohlen (z.B. von Andy Field Discovering Statistics Using SPSS), hier für die Paarvergleiche die Effektstärken zu berechnen. Dazu wird dann wieder das oben besprochenen r verwendet.
Kreuztabellen: Cramers V
Bei der Analyse von Kreuztabellen kann zur Berechnung der Stärke des Zusammenhangs Cramers V verwendet werden. Hier gilt ein Wert von 0.1 als klein, ein Wert von 0.3 als mittel und ein Wert von 0.5 als groß.
Korrelationen: Pearson- oder Spearman-Korrelationskoeffizient
Bei Korrelationen ist die Verwendung von Effektstärkemaßen Standard, denn gerade die Korrelationskoeffizienten sind die Maße für die Effektstärke. Hier verwendest du also einfach den Pearson- bzw. den Spearman-Korrelationskoeffizienten.
Hier gilt – genauso wie bei Cramers V – ein Wert von 0.1 als klein, ein Wert von 0.3 als mittel und ein Wert von 0.5 als groß.
Berechnung der Effektstärkemaße
Nicht alle Effektstärkemaße werden von der Statistiksoftware mit ausgegeben. In SPSS z.B. erhält man nicht direkt Cohens d. Teilweise muss die Berechnung extra angefordert werden, z.B. bei Eta-quadrat in der einfaktoriellen ANOVA.
Auf der Internetseite http://www.psychometrica.de/effektstaerke.html kannst du dir viele Maße online berechnen und findest außerdem weitere Informationen zur Interpretation und Referenzen zum Zitieren.
Kennst du weitere Quellen und Tools zur Effekstärke?
Quellen:
- Andy Field, Discovering Statistics Using SPSS, Sage, 2013
- Online Tool zur Berechnung von Effektstärken und Referenzen zur Interpretation: http://www.psychometrica.de/effektstaerke.html
Die 10 häufigsten Fehler bei Abschlussarbeiten mit SPSS und wie du sie vermeidest.
Hol dir jetzt die Liste für 0,- Euro und komm mit deiner Datenanalyse fehlerfrei und schnell voran!

Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.





Liebe Daniela,
ich habe zwei Mann-Whitney-U-Tests gerechnet und die jeweiligen z-Werte in die Formel eingesetzt. Jetzt bekomme ich zwei negative Effektgrößen:
r= -0,40
r= -0,3
Was sagt mir das negative Vorzeichen? Kann ich das Vorzeichen ignorieren und einen mittleren Effekt annehmen?
danke im Voraus und beste Grüße
Klara
Ja. 🙂
Schöne Grüße
Daniela
Liebe Daniela,
ich habe einige U-Tests für die ich die Effektgröße berechnen möchte. Gibt es bei SPSS eine Möglichkeit das r zu berechnen?
Hallo Lulu,
das geht nicht direkt in SPSS. Kannst Du aber mit obiger Formel schnell von Hand machen.
Weitere Fragen könnt Ihr gern in meiner Facebook-Gruppe Statistikfragen https://www.facebook.com/groups/785900308158525/ diskutieren.
Schöne Grüße
Daniela
Hallo Daniela,
eine Frage hätte ich noch: Gibt es denn einen Unterschied zwischen dem partiellen Eta Quadrat und dem Eta Quadrat? Also ist es egal, wie ich es bei der Ergebnisdarstellung bezeichne? Meine Frage bezieht sich auf Welch- Tests und ANOVAs. Vielen Dank
Hallo Denise,
das partielle Eta-Quadrat wird in der mehrfaktoriellen ANOVA verwendet.
Schöne Grüße
Daniela
Kleiner Auszug aus einer meiner Arbeiten zu eta und partiellen eta:
Pierce, Block und Aguinis (2004) weisen in ihrer Arbeit darauf hin, dass in vielen Studien das partielle eta² mit dem klassischen eta² verwechselt wird und es so zu einer Überschätzung der tatsächlichen Effekte kommt.Cohen (1973), der vermutlich die Begriffe „klassisch“ und insbesondere „partiell“ begründet hat, beschreibt, für welchen Zweck welches Effektmaß geeignet ist. Werden Variablen systematisch variiert, kann ihr Einfluss nicht als Fehler gesehen werden und findet somit keinen Eingang in die Residual‐ (oder Fehler‐) Varianz. Daher sollte in einem Setting für die Effekte einzelner Faktoren und Faktorkombinationen das partielle eta² genutzt werden, da dann der Einfluss der übrigen
Faktoren entfernt („auspartialisiert“) und so ein Vergleich des Effektes über verschiedene
Experimente hinweg ermöglicht wird. Auch der Einfluss konstant gehaltener Variablen soll auspartialisiert werden, da auch sie die Residualvarianz nicht beeinflussen. Werden hingegen Variablen als Kontrollvariablen eingeführt, gehören sie ja per Definition zur (allerdings kontrollierten) Residualvarianz im experimentellen Setting. In diesem Fall ist das klassische eta² zu verwenden. In gemischten Designs mit experimentellen Faktoren und Kontrollvariablen sollte dementsprechend ein dem Design angepasstes („custom‐tailored partial eta²“, Cohen, 1983, S. 111) Effektmaß genutzt werden.
Herzlichen Dank für die Ergänzung!
Schöne Grüße
Daniela
Hallo, Daniela!
Das Buch von Andy Fields liegt mir als Bibel vor und ich habe jetzt diesen Beitrag gelesen, wobei sich mir doch eine Frage aufwirft.
Auf Seite 332 bei Fields wird die Effektgröße über den abhängigen t-test nach Rosental wie folgt empfohlen:
r =SQR(t^2/(t^2+df))
wobei sich nach Seite 50 bei Fields nach Cohen wie folgt darstellt:
r = .10 als kleiner Effekt, welcher 1% der Gesamtvarianz erklärt
r = .30 als mittlerer Effekt, welcher 9% der Gesamtvarianz zählt
r = .50 als kleiner Effekt, welcher 1% der Gesamtvarianz zählt
Diese hätte ich auch bei Benesch, 2013 so herausgelesen.
Dies hätte doch auch den Vorteil, das die Skala auch zum Effektwert der Mediane (der bei Fields ident ist) vergleich bar ist.
Sehe ich dies falsch?
Danke für Deine Hilfe im voraus!
Hallo Jürgen,
danke für die Ergänzung! Ja, das passt so. Allein bei r=.5 wird 25 % der Gesamtvarianz erklärt.
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für die gut verständliche Erklärung!
Was ich mich noch frage ist, ob man Cohens d auch heranziehen kann, wenn man explorativ (bei bereits vorliegenden Daten) Mittelwerte miteinander vergleichen möchte; man also vorher keine Hypothesen hat.
Beste Grüße
Tini
Hallo Tini,
ja, dafür passt er sehr gut.
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für die verständliche Erklärung! Mich würde noch interessieren, ob ich Cohens d auch bei einem explorativen Vergleich von zwei Mittelwerten berechnen kann. Also ohne, dass ich vorher eine Hypothese über den Ausgang dieses Vergleichs aufgestellt habe.
Beste Grüße
Tini
Hallo Tini,
ja, das geht!
Schöne Grüße
Daniela
Hallo Daniela,
hier: https://statistik-und-beratung.de/2013/08/post-hoc-tests-und-fehlerkorrektur/ schreibst du unter der Frage vom 23.April 2015, dass man die Power oft dann wissen wolle, wenn Unterschiede vorliegen, aber nicht signifikant werden. Hier wiederum sagst du, die brauche man, um Zusammenhänge einschätzen/interpretieren zu können – also auch bei vorliegen von Signifikanz. Das verwirrt mich etwas, ist das nicht widersprüchlich?
Zum Eta-Quadrat der ANOVA und SPSS: Ich benutze SPSS 23 – da kann man das nicht unter Optionen anklicken. Ist es möglich, sich das irgendwie über eine Syntax auswerfen zu lassen?
Danke und Gruß,
Lisa
Hallo Lisa,
Power und Effektstärke sind zwei unterschiedliche Dinge.
Eta-Quadrat kann man sich beim Menü zur Univariaten ANOVA anklicken (bei mir in SPSS 22, das müsste in SPSS 23 genauso sein).
Schöne Grüße
Daniela
Sehr geehrte Frau Keller,
Dunlap, Cortina, Vaslow, & Burke (1996) argumentieren, dass Cohen´s d bei repeated measures designs nach der Formel d = tc [2(1 − r)/n]1/2 berechnet werden soll, wobei tc = korrelierte t-Statistik für abhängige Stichproben, r = Korrelation zwischen t1 und t2 und n = Stichprobengröße pro Gruppe. Dies soll eine potenzielle Überschätzung der Effekte, die die Standardformel nach Cohen verursacht (d = (Mt1–Mt2)/SDpooled, wobei SDpooled = (SDt12–SDt22) ½/2), verhindern. Leider gibt es auf der Seite Psychometrica keine Option, sich Konfidenzintervalle hierfür ausgeben zu lassen. Sehen Sie eine einfache Möglichkeit, diese zu berechnen?
Vielen Dank und herzliche Grüsse!
Hallo Leslie,
habe nach kurzer Recherche dazu leider nichts gefunden. Ich würde bei der Software R weiter suchen, da gibt es erfahrungsgemäß so ziemlich alles. Wenn Du Dich mit R befassen willst, lohnt sich die Suche dort!
Schöne Grüße
Daniela
Hallo,
ich habe eine Frage, ich rechne für meine Masterarbeit eine ANOVA mit Messwiederholung (3 Messzeitpunkte) und soll dafür Effektstärken angeben.
Das partielle eta² habe ich mir einfach von SPPS mit ausgeben lassen. Jedoch soll ich aufgrund meiner kleinen Stichprobe lieber omega² verwenden, kann ich das auch ausgeben lassen oder aber eta² in omega² umrechnen?
Und zweitens soll ich auch d, bzw. (aufgrund der kleinen SP) g berechnen. Dafür muss ich mir doch aber gezielt Kontraste anschauen, um die Mittelwerte von zwei speziellen Messzeitpunkten miteinander vergleichen zu können? Und gibt es eine Umrechnungsformel von d in g?
Danke schonmal und ein großes Lob für die tolle Seite!
Hallo Lisa-Maria
Soweit mir bekannt ist gibt SPSS nicht diekt (wie bei eta²) ein omega² heraus, aber du kannst dies ganz einfach berechnen, wenn du eine ANOVA hast.
w²=(SSb – dfbMSw)/(SSt + MSw)
SSt ist total sum of squared.
SSb ist sum of squares between groups
SSw ist sum of squares within groups
dfb ist degrees of freedom between groups
MSw ist mean sum of squares within groups (SSb/dfb)
Zu deiner 2. Frage:
d und eta² sagen im Grunde das selbe aus. Allerdings hast du mehr als 2 Gruppen und musst daher das partielle eta² benutzen. Durch deinen kleine Stichprobenumfang nimmst du omega², da dadurch weniger Verzerrungen auftauchen, da es die Anzahl der Gruppen bei der Berechnung der Varianzaufklärung miteinbezieht.
Ich hoffe ich konnte helfen.
Liebe Grüße
Theresa
Liebe Frau Keller
Erst Mal ein herzlicher Dank für Ihre super Seite, die ist für mich Gold wert!
Ich bin derzeit gerade an meiner Masterarbeit und hab das Problem, dass meine Stichprobe extrem klein ist, d.h. die Wahrscheinlichkeit, dass ich überhaupt ein signifikantes Ergebnis erhalte, sehr klein ist. Nun zieh ich zur Interpretation der Effekte die Effektstärke bei. Je nach Test ist das Cohen’s d, Rosenthal’s r (beim Mann Whitney Test) oder Eta-Quadrat.
Nun bin ich mittlerweile aber völlig verwirrt, ob und wann das überhaupt angebracht ist, und hab drei Fragen:
1) Die Effektstärke ist ja auch von der Power und der Stichprobengrösse abhängig. Ist die kleine Stichprobengrösse in der Effektstärke bereits berücksichtigt, oder ist die genauso wenig aussagekräftig wie Signifikanztests?
2) ist es sinnvoll, bei nicht signifikanten Ergebnissen überhaupt die Effektstärke zur Interpretation beizuziehen.
3) Wenn der Signikanztest negativ ausgefallen ist, die Effektgrösse einen mittleren Effekt anzeigt, ist es dann korrekt zu schreiben: ..ergab einen mittleren, nicht signifikanten Effekt“? Oder bedeutet das, das die Effektstärke selber nochmals mittels Konfidenzintervallen auf die Signifikanz überprüft worden ist?
Falls Sie Zeit haben, diese Fragen kurz zu beantworten, bin ich natürlich sehr dankbar. Hab grad wirklich ein riesen Durcheinander.
Liebe Grüsse
Rahel
Hallo Rahel,
zu 1) Nein, die Effektstärke ist nicht von der Power und Stichprobengröße abhängig.
zu 2) Ja.
zu 3) Ja, die Formulierung ist so passend. Zusätzlich Konfidenzintervalle brauchst du nicht.
Für weitere spezielle Fragen kannst du meine Facebookgruppe Statistikfragen nutzen: https://www.facebook.com/groups/785900308158525/
Schöne Grüße
Daniela
Liebe Daniela,
ich habe noch eine Frage zur Formel für die Unterschiedsmessung zwischen zwei Medianen (r=z/Wurzel N). Muss ich bei einer Vorher-Nachher-Messung die Fallzahl N der Gruppe (N=40), die ich vorher und nachher vergleiche, verdoppeln auf 80?
Ich freue mich sehr über einen Tipp!
Ja.
Hallo Daniela!
Deine Seite ist wirklich Gold wert, habe hier schon einige nützliche Erkenntnisse für meine Dissertation gewinnen können, vielen Dank dafür!
Ich hätte jedoch zu diesem Thema ein paar Fragen, vielleicht kannst du mir da ja auch weiterhelfen?
Ich möchte Lebensqualitätsdaten in einer Längsschnittstudie an 4 Zeitpunkten (vor einer OP + 3mal danach) mit immer derselben Gruppe (n=100) auswerten. Die einzelnen Domänen haben entweder 4 oder durch Zusammenrechnung bis zu 11 Antwortmöglichkeiten, die dann in Mittelwerte auf einer Skala von 0-100 umgerechnet werden. Das macht die Daten ja nicht gerade für eine „Normalverteilung“ prädestiniert, die QQ-Diagramme sehen aber meistens sogar gut aus, jedoch häufig mit signifikanter Schiefe. Also denke ich wäre trotzdem der Wilcoxon-Test Mittel der Wahl, wenn ich einen Unterschied zwischen 2 Zeitpunkten untersuchen will. Soweit so gut, jetzt wird es für mich tricky: Um die klinische Relevanz anzugeben sind nur Verfahren, die über den Mittelwert gehen geläufig (zB 10 Punkte Unterschied = klinisch relevant) oder Effektstärken, die auf mich deutlich sinniger erscheinen.
1) Nützen Effektstärken überhaupt, wenn man keine Normalverteilung hat? Oder geht man dann irgendwie doch von einer Normalverteilung aus?
2) Wie berechne ich die Effektstärke in diesem Fall? Muss man das über den Wilcoxon-Test machen oder kann man (wie ich es in einer anderen Studie mit demselben Fragebogen gesehen habe) einfach die Differenz der Mittelwerte durch die SD nehmen?
3) Falls letzteres zutreffen sollte, habe ich die Unterscheidung zwischen Cohen und Glass gefunden, mit der Empfehlung für Glass (aka BaselineSD weil man davon ausgeht, dass sie am wenigsten durch die Therapie=Op beeinflusst ist) falls es zu große Varianzunterschiede gibt. Leider gibt es bei mir große Unterschiede in der Varianzhomogenität in den einzelnen Domänen. Meine Idee wäre nun das jeweils bessere Verfahren für die einzelnen Domänen zu wählen. Macht das Sinn und ab wann wäre denn ein Varianzunterschied „zu groß“? Mir fehlen da leider jegliche Erfahrungswerte!
Liebe Grüße!
Hallo,
wie in dem Beitrag genannt, gibt es auch für nichtparametrische Verfahren passende Effekstärken. Sie berechnen sich aus der Teststatistik und der Fallzahl, siehe Formel im Beitrag.
Wenn die Q-Q-Diagramme aber gut aussehen, kannst du wohl auch von Normalverteilung ausgehen. Die Tests auf Normalverteilung sind bei großer Fallzahl zu streng.
Schöne Grüße
Daniela
Sehr geehrte Frau Keller,
im Rahmen meiner Masterarbeit untersuche ich gerade ob im Rahmen eines Ergometertestes der Proband die linear steigenden Leistungsvorgaben einhalten kann bzw. wie genau. Ich habe also pro Proband/Versuchsreihen (N=51) eine Messreihe über ca. 160-200 Werte mit der realisierten Leistung und der vorgegebenen Leistung. Mein erster Ansatz wäre die Geradengleichung (speziell der Anstieg) der Ist-Werte zu bestimmen und mit der Geradengleichung der Soll-Werte zu vergelichen. Weiterhin hatte ich an ein Bland-Altman-Plot gedacht um zu überrüfen wie genau die Leistungforgaben eingehalten werden. Ein weiteres Problem ist wie ich die 51 Versuchreihen zusammenbringe/zusammenfassend bewerte?
Über Tips und Lösungsansätze währe ich sehr dankbar.
Hallo Kay,
so genau ist mir deine Problemstellung noch nicht klar. Du bekommst für jeden Probanden einen Wert (Anstieg), den du mit einem Ist-Wert vergleichen willst?
Schöne Grüße
Daniela
Hallo Daniela,
vielen Dank für Deinen tollen Beitrag über Effektstärken! Ich beschäftige mich derzeit mit diesem Thema und habe eine Frage.
Du schreibst für Cohens d in der Formel, dass die Differenz der Mittelwerte durch die Standardabweichung der Kontrollgruppe zu teilen ist.
Jetzt lese ich allerdings in einigen Büchern, dass die Differenz der Mittelwerte durch die gepoolte Standardabweichung geteilt werden muss.
Meine Frage: Wonach entscheide ich, wann ich die Standardabweichung der Kontrollgruppe zu nehmen habe oder wann sollte ich lieber die gepoolte Standardabweichung zur Berechnung verwenden?
Auf Psychometrica heißt es: „Sind die Standardabweichungen beider Gruppen sehr unterschiedlich, so schlägt Glass vor, nicht auf die gepoolte Standardabweichung zurückzugreifen, sondern auf die Standardabweichung der Kontrollgruppe.“
Ab wann sind meine Standardabweichungen jedoch als „sehr unterschiedlich“ anzusehen?
Vielen Dank im Voraus für Deine Antwort.
Schöne Grüße,
Canan
Hallo Canan,
ja, diese Formeln gibt es beide. Und wie bei Psychometrica empfohlen, macht es Sinn, die gepoolte Standardabweichung zu verwenden, wenn sich die beiden sehr unterscheiden. Das „sehr unterscheiden“ ist nicht definiert. Es gibt dafür Tests (Levene) die untersuchen, ob sie sich signifikant unterscheiden. Aber abhängig von der Fallzahl sagt das auch nichts darüber aus, ob sie sich „stark“ unterscheiden. Insofern ist das eine subjektive Einschätzung. Wichtig ist immer, dass man dokumentiert und berichtet, wie man vorgegangen ist.
Schöne Grüße
Daniela
Hallo Daniela!
Ganz toller Blogeintrag!
Sehr kondensiert und eine gute Basis um Effektstärken zu verstehen.
ProTipp: Grafiken veranschaulichen die ganze Geschichte.
Keep up the good work,
FP
Hallo FP,
danke für das Feedback und den Tipp!
Schöne Grüße
Daniela
Sehr geehrte Frau Keller,
erstmal großes Lob für Ihre Tätigkeit. Ich bin mir unsicher was das Reporting von Effektstärken angeht. Manchmal lese ich als Abkürzung für die ES d,w, etc. Konkret: Welche Effektstärkeabkürzung verwende ich bei Korrealtionen (Spearman und Pearson), Anovas (einfaktorielle Varianzanalyse mit Messwiederholung), Friedmann, t-test und Wilcoxon?
Vielleicht könnten Sie mir hierbei behilflich sein?
Hallo Salvatore,
d steht für Cohens d und wird für Mittelwertvergleiche verwendet, deshalb gehört es zum t-Test.
eta-quadrat ist das Effektstärkemaß für die ANOVA (Gruppenfaktor und/oder Messwiederholung, ein- oder mehrfaktoriell), das von SPSS auch ausgegeben wird. Manche empfehlen, stattdessen omega-quadrat (w²) zu verwenden, das weniger Bias haben soll (ich vermute, das hast du mit w gemeint).
Für Wilcoxon und Mann-Whitney U wird ein r aus Z und N berechnet, das wird also mit r bezeichnet.
Für Friedman und Kruskal-Wallis ist die Berechnung sehr komplex, wird selten verwendet.
Bei Korrelationen wird meist r für Pearson und rho für Spearman verwendet.
Schöne Grüße
Daniela
Liebe Daniela,
toller Beitrag! Genau das habe ich gesucht 🙂
Zwei kleine Fragen:
1) Auf der Internetseite „psychometrica“ habe ich mir das Cohen´s d berechnen lassen. Hierfür habe ich einmal die Berechnung „2. Mittelwertsunterschiede zweier verschieden großer Gruppen (Cohen’s d, Hedges‘ g)“ und das andere mal zur Kontrolle „4. Berechnung der Effektstärke bei abhängigen und unabhängigen t-Tests“ verwendet. Die Zahl war zwar bei beiden Berechnungsarten gleich, aber bei der einen Berechnung hatte ich ein negatives und bei der anderen ein positives Vorzeichen. Für die Interpretation macht das aber nicht aus oder? Da sowohl der Minus als auch Plus- Bereich gleich interpretiert wird (sprich 0,2 oder -0,2 –> beides steht für einen niedrigen Effekt)
2) Wenn ich aufgrund von ungleichen Varianzen den Welch-Test verwendet habe, welches Effektstärkemaß benötige ich hierfür?
Hallo,
schön, dass der Beitrag so gut passt! 🙂
zu 1): das negative Vorzeichen bedeutet, dass die Reihenfolge der verglichenen Gruppen anders ist. Für den Unterschied selbst ist das irrelevant. Es liegt nur daran, welche Gruppe als erste Gruppe und welche als zweite Gruppe betrachtet wird.
zu 2): Hier kannst du die gleichen Methoden wie beim t-Test verwenden, also d aus Mittelwerten und SDs berechnen oder direkt aus der Teststatistik.
Schöne Grüße
Daniela