Bei metrischen Variablen gibt es verschiedene Möglichkeiten in einer Abbildung zu veranschaulichen, inwieweit sich zwei Stichproben unterscheiden. Entscheidend ist hier, dass ein Maß für die Streuung mit verwendet wird (z.B. als Fehlerbalken). Bei nichtschiefen Verteilungen eignen sich dafür z.B. die Standardabweichung (standard deviation, SD), der Standardfehler des Mittelwerts (standard error of the mean, SEM) und das 95%-Konfidenzintervall (95% confidence interval, 95%-CI).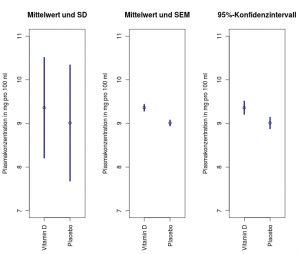
Abbildung der Daten aus Vitamin D Studie (Cockburn et al., 1980): Mittelwerte der Plasmakonzentrationen von Neugeborenen mit SD, SEM und Konfidenzintervall.
Standardabweichung
Sehr geläufig ist die Standardabweichung. Sie beschreibt die Schwankung der Messwerte um den Mittelwert und ist die größte der drei hier vorgestellten Messwerte. Sie wird gerne angegeben, da sie direkt verwendet werden kann, um Signifikanztests auf die Daten zu berechnen. Allerdings gibt sie graphisch keinen direkten Hinweis auf Gruppenunterschiede.
Du willst mehr Durchblick im Statistik-Dschungel?
Standardfehler des Mittelwerts
Der SEM ist der kleinste Wert hier. Vielleicht wird er deshalb gerne in Grafiken eingesetzt, um einen nicht so deutlichen Unterschied deutlicher erscheinen zu lassen?!
95%-Konfidenzintervall
Das 95%-Konfidenzintervall ist meiner Meinung nach die wertvollste Möglichkeit der Darstellung von Streuung in solch einer Abbildung, denn es gibt einen direkten Zusammenhang zum p-Wert eines Signifikanztests: Überlappen sich die beiden Konfidenzintervalle in der Abbildung nicht, so ist der p-Wert des Tests kleiner 0,05 und es gibt einen signifikanten Unterschied zwischen den beiden Gruppen.
Referenzen
Cockburn et al. (1980). Maternal vitamin D intake and mineral metabolism in mothers and their newborn infants. Br. Med. J., 281, 11-14.
Stuart J. Pocock (1983). Clinical Trials. A Practical Approach. John WIley & Sons.

Ich bin Statistik-Expertin aus Leidenschaft und bringe Dir auf leicht verständliche Weise und anwendungsorientiert die statistische Datenanalyse bei. Mit meinen praxisrelevanten Inhalten und hilfreichen Tipps wirst Du statistisch kompetenter und bringst Dein Projekt einen großen Schritt voran.





Wie interpretiere ich bei n=240 mean 2.12 und sd 2.26
Hallo Bernd,
das kommt darauf an, ob die Daten normalverteilt sind und was das Ziel Deiner Untersuchung ist. Was willst Du herausfinden?
LG Daniela
Hallo,
im Rahmen meiner Arbeit bin ich da gerade auf etwas gestoßen, bei dem ich keine so wirklich Antwort finden kann…
Und zwar habe ich ein Ergebniss, das in Prozent angegeben wird. z.B. „Es sind 10% der Fläche mit etwas bedeckt“. Jetzt würde ich in diesen Satz gerne noch den SEM einbauen. Dabei sind die Fragen.
a) Darf man das überhaupt? Wenn ja:
b) Gibt man das als +/- SEM dann an oder nur als +SEM?
c) Wird der SEM dann auch in % angegeben oder nur als Zahl ohne Wert?
Ich würde mich sehr über eine Antwort freuen.
MFG
Sandra
Hallo Sandra,
zu a) Ja.
zu b) +/-SEM.
zu c) Auch in % finde ich besser.
Schöne Grüße
Daniela
Ok, nur kurz als Rückmeldung:
Meine Erstbetreuerin meinte, dass für sie der Satz auch ok wäre, dass „das Vorgehen bei der Berechnung von signifikanten Unterschieden zwischen binär-basierten Kappa-Werten wird immer wieder gern diskutiert wird…“
Liebe Grüße und danke nochmal,
Hanna
Weiterführende Fragen könnt ihr gern mit mir und den anderen Teilnehmern in der Facebook-Gruppe Statistikfragen diskutieren. Hier der Link: https://www.facebook.com/groups/785900308158525/
Liebe Daniela,
im Rahmen meiner Abschlussarbeit beschäftige ich mich mit der „Interraterreliabilität von Elicitation-Interviews in einer Langzeitmeditationsstudie“, wobei ich die Interraterreliabilität (2 Rater) mittels Cohens Kappa berechnet habe.
Die Kodierung in SPSS erfolgte auf Nominaldatenniveau mit 3 Ratingkategorien. Berechnet habe ich Kappa…
– insgesamt für alle Interviews
– gesondert für einen Teil der Interviews der schwächer strukturiert war
– gesondert für einen Teil der Interviews der stärker strukturiert war
– und alle Berechnungen auch ohne Einbezug von missing values
Die unterschiedlichen Kappa-Werte hab ich mithilfe des 95%-Konfidenzintervalls (habe ich manuell berechnet) verglichen. Nun möchte ich gerne eine Graphik erstellen um die Überlappungen der verschiedenen Konfidenzintervalle zu veranschaulichen. Leider bin ich auch nach stundenlangem Ausprobieren noch ratlos wie:-(
Auch ist es mir bisher nicht gelungen ein Diagramm (Clustered Bar Chart) zur Häufigkeits-Verteilung der 3 Ratingkategorien „ja“, „nein“ und „missing value“ zu erstellen, in dem Rater 1 und Rater 2 zum Vergleich jeweils nebeneinander erscheinen
Danke,
Hanna
Ok, ich hab das ganze jetzt einfach – anstatt in SPSS – im Tabellenkalkulationsprogramm „Numbers“ gemacht:-), da hab ich’s hinbekommen.
Aber bzgl. eines Satzes aus meiner Bachelorarbeit wäre ich noch über ein Feedback sehr dankbar…ich zweifle ob das so korrekt ausgedrückt ist:
>> Als signifikant unterschiedlich galten die Kappa-Werte dann, wenn die Konfidenzintervalle keine gemeinsame Schnittmenge aufwiesen.<<
(für Background siehe Ursprungsbeitrag)
In meinem Falle mit den dichotomen Variablen (i.e. nur Ja-Nein-Antworten) gibt es ja in Wirklichkeit keine sich überlappende Verteilungen. Die Konfidenzintervalle wurden ja von einem Chi-Quadrat Test berechnet, nicht mit einem exakten Test nach Fisher. Aber ich bin etwas ratlos wie ich den Satz richtig formulieren kann…
Danke,
Hanna
Hallo Hanna, gut, dass du die Abbildung hinbekommen hast! Die Konfidenzintervalle sind für die Schätzung des Kappa-Werts: Unterscheiden sich die Kappa-Werte? Die könnten ja schon gleich oder ähnlich sein, auch bei ja/nein-Antworten… Der so formulierte Satz passt für mich!
Liebe Daniela,
danke für Deine Antwort!
Jetzt hab ich bzgl. des Satzes zwei gegensätzliche Meinungen von zwei unterschiedlichen Statistikexperten;-)
Nein, die Kappa-Werte unterscheiden sich gemäß der 95%-Konfidenzintervalle nicht signifikant.
Liebe Grüße,
Hanna
🙂 Dann brauchst du vielleicht noch eine dritte und schaust, wer gewinnt! 😉
Hallo Daniela,
ich habe Daten die nicht normalverteilt sind.
Die Standardabweichung liegt bei 7,36 nun möchte ich eine vergleichbare Aussage treffen zu:
„Bei einer Normalverteilung wären 4,6 % der Daten außerhalb von 2 Standardabweichungen.“
Wieviel Prozent wären bei meinen Daten dann außerhalb von 2 Standardabweichungen? Was muss ich da rechen, wenn eben keine Normalverteilung vorliegt?
Danke, Maria
Hallo Maria,
wenn keine Normalverteilung vorliegt, gibt es keine solche Regel.
Alternativ könnten Sie mit Quantilen arbeiten. Wenn Sie sich z.B. das 5 %- und das 95 %-Quantil berechnen, wissen Sie, dass unter dem einen 5 % der Beobachtungen und über dem anderen auch 5 % der Werte liegen.
Schöne Grüße
Daniela Keller