Wenn Du eine mehrfaktorielle ANOVA rechnest, solltest Du Profilplots betrachten, um mögliche Interaktionen richtig zu interpretieren. Dies ist besonders wichtig, wenn Du eine signifikante Interaktion erhälst, Du aber die Haupteffekte (also die einzelnen Faktoren) interpretieren willst. Es ist nämlich möglich, dass eine signifikante Interaktion einen Haupteffekt stört und damit nicht interpretierbar macht. Ob das der Fall ist, untersuchst Du mit Profilplots.

Was ist ein Profilplot?

In einem Profilplot sind die Mittelwerte der abhängigen Variable für die einzelnen Kategoriekombinationen Deiner Gruppenfaktoren getrennt dargestellt. Dabei befinden sich die Kategorien des einen Gruppenfaktors an der x-Achse, die des anderen Gruppenfaktors in einer farbigen Lebende (ich gehe der Einfachheit halber davon aus, dass es sich um eine ANOVA mit zwei Faktoren handelt). An der y-Achse ist die abhängige Variable angetragen.

Bei einer zweifaktoriellen ANOVA erstellst Du zwei Profilplots. Im ersten Profilplot ist Faktor A an der x-Achse und Faktor B als farbiger Code in der Legende. Im zweiten Profilplot ist es umgekehrt.

Was kann ich am Profilplot ablesen?

Du untersuchst am Profilplot, ob die Haupteffekte Deiner beiden Faktoren in der berechneten ANOVA interpretierbar sind. Kreuzen sich die Linien der Kategorien eines Faktors, so ist der Haupteffekt durch die Interaktion gestört und nicht wie in der ANOVA berechnet interpretierbar.

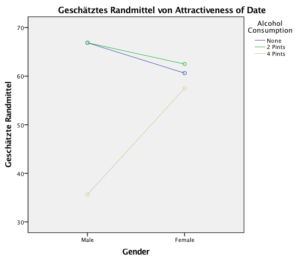
In den obigen Beispielen wird in Abbildung 1 untersucht, ob der Haupteffekt des Faktors „Alcohol Consumption“ interpretierbar ist. Dazu betrachtest Du das Bild um zu sehen, ob sich die Linien kreuzen. Das tun sie nicht (oder nur sehr knapp). Das bedeutet, dass die Reihenfolge der mittleren Ausprägungen der abhängigen Variable in den Kategorien des Faktors „Alcohol Consumption“ bei jeder der Kategorien des Faktors „Gender“ gleich bleibt: grün hat immer den höchsten Wert, blau den zweithöchsten und gelb den niedrigsten Wert. Damit ist der Haupteffekt von „Alcohol Consumption“, der in der ANOVA berechnet wurde, interpretierbar, auch wenn die Interaktion signifikant ist. Die Interaktion stört den Haupteffekt nicht.

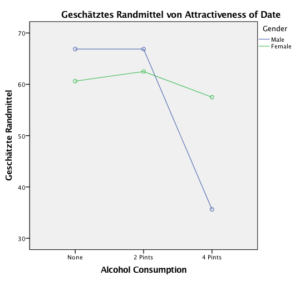
Anders ist das in Abbildung 2. Hier ist Legende und x-Achse nun vertauscht. Die Linien beschreiben die Kategorien des Faktors „Gender“. Hier kreuzen sich die Linien. Das bedeutet, die Reihenfolge der beiden Gender-Kategorien ist nicht in jeder Kategorie von „Alcohol Consumption“ gleichbleibend. Mal hat Male höhere Werte, mal hat Female höhere Werte. Damit ist der Haupteffekt von „Gender“, der in der ANOVA berechnet wurde, nicht interpretierbar, wenn die Interaktion signifikant ist. Die Interaktion stört den Haupteffekt.

 

 

Die Linien kreuzen sich. Was nun?

Noch einmal: das Kreuzen der Linien im Profilplot ist nur ein Problem wenn

1. die Interaktion signifikant ist und
2. Du an der Interpretation der Haupteffekte interessiert bist.

Zudem ist immer nur der Haupteffekt nicht interpretierbar, bei dem sich die Kategorien-Linien im Profilplot kreuzen. So wie im obigen Beispiel ist der Haupteffekt von „Alcohol Consumption“ sehr wohl interpretierbar, weil sich die Alcohol-Consumption-Linien nicht kreuzen. Der Haupteffekt von „Gender“ ist nicht interpretierbar, weil sich die Gender-Linien kreuzen. Beide gehören aber zur gleichen Interaktion!

Wenn Du aber nun einen Haupteffekt, wie zum Beispiel hier den von „Gender“ interpretieren willst und weißt nun durch die Profilplots, dass Du dafür das Ergebnis der ANOVA nicht verwenden kannst, dann solltest Du Deine Daten sinnvoll aufteilen und den Haupteffekt von Gender auf Teildatensätzen untersuchen. In dem Beispiel bietet es sich an, den Datensatz nach den Kategorien der „Alcohol-Consumption“ in zwei Teildatensätze zu teilen. Ein Teildatensatz kann „None“ und „2 Pints“ enthalten. Die Kategorie „4 Pints“ sollte im zweiten Datensatz liegen. Denn im zweiten Profilplot oben sieht man, dass sich der Gender-Effekt in diesen beiden Teildatensätzen völlig unterschiedlich verhält (einmal male höher und einmal female höher). Und das genau ist die Interaktion, die den Haupteffekt stört.

Du untersuchst also dann den Haupteffekt von „Gender“ auf diesen beiden Teildatensätzen und wirst bei beiden ein völlig unterschiedliches Ergebnis erhalten, das Du auch entsprechend interpretieren solltest. Wenn Du vorher eine zweifaktorielle ANOVA gerechnet hast, verwendest Du hier in dem Beispiel dann zwei t-Tests als Signifikantests (wenn Du mehrere Kategorien vergleichst, sind es mehrere einfaktorielle ANOVAs)

In dem Beispiel wirst Du als Ergebnis erhalten, dass im ersten Datensatz (also bei „None“ und „2 Pints“) die Männer (signifikant) höhere Werte als die Frauen erreichen. Im zweiten Teildatensatz ist es umgekehrt: (signifikant) höhere Werte bei den Männern.

Das hier verwendete Beispiel ist entnommen aus Andy Field, Discovering Statistics Using SPSS, Sage, 2014: Googles.