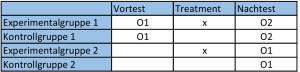
Der von Solomon entwickelte Versuchsplan ist eine Kombination zweier Kontrollgruppen-Versuchspläne, einmal mit und einmal ohne Vortest. Schematisch lässt sich dieser Versuchsplan wie folgt darstellen.
O1 = Beobachtungs- bzw. Messvorgang 1
O2 = Beobachtungs- bzw. Messvorgang 2
x = Einsatz einer exp. Variable
Ein Solomonplan untersucht, ob sich die durchschnittlichen Veränderungsraten und Experimental- und Kontrollbedingungen signifikant unterscheiden. Ein Beispiel für die Verwendung solcher Pläne wäre die Wirkungsnachweis eines Medikaments.
Unterscheiden sich Experimentalgruppe 1 und Kontrollgruppe 1 im Nachtest, so sind diese Differenzen auf präexperimentelle Unterschiede zurückzuführen. Das gleiche trifft auf Unterschiede zwischen Experimentalgruppe 2 undKontrollgruppe 2 zu. Unterscheiden sich Experimentalgruppe 1 und 2 im Nachtest, aber nicht im Vortest, sind Veränderungen auf die Maßnahme zurück zu führen. Auch hier gilt das gleiche für Differenzen zwischen den Kontrollgruppen 1 und 2. Bei ähnlich starken Veränderungen kann aber nicht mehr entschieden werden, ob Veränderungen auf die Spezifizität der Programme oder auf den Einsatz irgendeinesTreatments zurück zu führen sind (siehe Hawthorn-Effekt).
Bei einem Pretest-Posttest-Plan (Solomon-Plan) wird davon ausgegangen, dass es in den einzelnen Stichproben keine Unterschiede, hier z.B. Schweregrade einer Krankheit bestehen. Es werden lediglich die Besserungsraten der einzelnen Patienten berücksichtigt.
Auswertung eines Pretest-Posttest-Plans (Solomon-Plans)
- Durchführung eines U-Tests
- Differenz für jedes Individuum der Experimental- und Kontrollgruppe zwischen Pretest und Posttest ermitteln
- Rangreihe der Differenzen (=Pardifferenzen) erstellen
- U-Test für Paardiffernzen berechnen
Bei einer stärkeren Veränderung der Experimentalgruppe gegenüber der Kontrollgruppe sind die Differenzwerte und dadurch auch die Ränge der Experimentalgruppe größer als die der Kontrollgruppe und somit kann eine unterschiedliche Behandlungswirkung manifestiert werden (H1).
Du willst mehr Durchblick im Statistik-Dschungel?
Konkretes Beispiel:
Wir haben 2 konzentrationsfördernde Medikamente Methylphenidat (a1) und Metamphetamin (a2), die auf ihre Wirkung hin untersucht werden sollen. Hierzu werden in zwei Kliniken jeweils 5 hyperaktive konzentrationsgestörte und nach schulpsychologischen Empfehlungen zu behandende Kinder einmal vor und zweimal nach der Behnadlung auf ihre Konzentrationsfähigkeit untersucht.
H1: a1 und a2 unterscheiden sich.
H0: a1 und a2 sind gleich.
Signifikanzniveau: α=0,05
Testwahl: (Differenzen aus zwei unabhängigen Stichproben, unbekannte Verteilungseigenschaften der Differenzwerte) U-Test für Paardifferenzen
Es wird zunächst für jeden Schüler die Differenz aus den beiden Mesungen gebildet und anschließend eine Rangreihe (R(di)) nach dem U-Test für Paardifferenzen gebildet, sowie T1 und T2 ermittelt. Die Summe von T1 und T2 muss dann der Summe aller Zahlen von 1 bis N entsprechen, d.h. T1 + T2 = (N*(N+1)) / 2.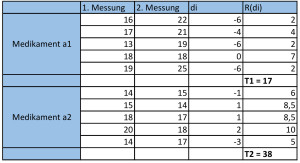
Aus den Rangsummen werden nun U-Wete berechnet.
U1= N1*N2 + (N1*(N1+1))/2 – T1 = 23
U2= N1*N2 + (N2*(N2+1))/2 – T2 = 2
Auch hier kann die Rechnug leicht überprüft werden:
U1 + U2 = N1 * N2
Für den Signifikanztest wird der kleinere der beiden U-Werte benötigt. Hier U2=2.
Für die Bestimmung der Überschrietungswahrscheinlichkeit, also dem p-Wert gibt es die Möglichkeit ein Tafelwerk oder ein Statistikprogramm zu nutzen. Der Befehl in R lautet:
wilcox.test(y1,y2,paired=FALSE)
In SPSS sollte folgendermaßen vorgegangen werden:
Klicksequenz: Analysieren > Nichtparametrische Tests > zwei unabhängige Stichproben
Syntax: NPAR TESTS M-W
Der ermittelte p-Wert gibt beim statistischen Test die Wahrscheinlichkeit an, mit der sich unter der Nullhypothese die gefundenen oder noch extremere Ereignisse einstellen. Ist der p-Wert kleiner als das festgelegte Signifikanzniveau kann die Nullhypothese verworfen werden. Anderenfalls besteht auf dem vorgegebenen Signifikanzniveau kein Widerspruch zur Nullhypothese. Je kleiner der p-Wert (somit je geringer die Wahrscheinlichkeit, H0 fälschlicherweise zu verwerfen), desto eher sollte man die Nullhypothese verwerfen und umgekehrt.
In unserem Beispiel ist der p-Wert 0,016. Da es sich um einen zweiseitigen Test handelt ist p mal 2 zu nehmen, also p´= 0,032.
Entscheidung: Die H0 ist zu verwerfen, da p<α.
Interpretation: Medikament a1 wirkt offenbar beim hyperkinetischen Syndrom von Schulkindern in höherem Maße konzentrationsfördernd als Medikament a2.
Fazit: Pretest-Posttest-Pläne (Solomon-Pläne) sind sehr hilfreich um den Überblick bei einem Test zu bewahren und schnell zu einem Ergebnis zu kommen.
Ich bin Studentin der Betriebswirtschaftslehre an der FHWS und habe zuvor ein Studium der Empirischen Bildungsforschung und der Sonderpädagogik an der Julius-Maximilians-Universität Würzburg absolviert. Statistik begeistert mich! Besonders die freie Statistiksoftware R hat es mir angetan. Deshalb schreibe ich hier ab und zu im Blog von Statistik & Beratung kleine Beiträge zu Statistikthemen und deren Umsetzung in R. Ich freue mich auf euer Feedback und eure Kommentare!




Hallo Theresa, ich habe eine Frage zu Solomon-Plänen:
Wenn ich Verändersunterschiede zwischen zwei gruppen mit einem Solomon-Design beurteile und dies anhand von 3 verschiedenen variablen ( e.g. 3 Parameter zur Beurteilung der körperlichen Leistungsfähigkeit) tue, muss ich dann eine Testkorrektur für multiples testen durchführen? Oder ist das nur nötig wenn ich mehr als 2 Gruppen vergleiche?
danke
Hallo Florian, entschuldige, dass du so lange warten musstest. So lange du nur eine Hypothese testest brauchst du keine Testkorrektur durchzuführen. Hilfreich ist auch die Seite https://statistik-und-beratung.de/2013/08/post-hoc-tests-und-fehlerkorrektur/ von Daniela.
Ich hoffe ich konnte helfen. LG Theresa
Hallo Theresa,
Also ich habe für die Veränderung jeder der drei Variablen eine einzelne Nullhypothese (=kein Unterschied zwischen den Gruppen) aufgestellt.
Meine Vermutung ist, dass sich alle drei variablen in der testgruppe stärker verändern als in der Kontrollgruppe.
Das heist ich müsste dann noch für 3-fache Testung korrigieren ?
vielen Dank.
PS: ich habe inwzischen rausgefunden, dass die gemessenen parameter laut referenzliteratur stark miteinander korreliert sind (r=0.9). Ist mein Vorgehen dann überhaupt sinnvoll, mehrere Parameter zu prüfen die sowieso miteinander zusammen hängen ?
Wäre super wenn du mir weiter helfen könntest.
Hallo Florian, Du musst es, wie richtig festgestellt auf dreifache Testung ändern und trotz des starken Zusammenhangs – auf Grund der Tatsache, dass aus einem starken Zusammenhang nicht folgt, dass es auch eine eindeutige Ursache-Wirkungs-Beziehung gibt, die Parameter nutzen.
Ich hoffe ich konnte helfen. LG
Hallo Theresa,
ich habe ebenfalls einen Prätest und einen Posttest durchgeführt. Dazwischen lagen zwei unterschiedliche Treatments. Bei dem Vergleich der Prätest-Daten durch den U-Test fällt außerdem auf, dass sich die Ausgangsdaten schon signifikant unterscheiden. Dieser Unterschied vergrößert sich nochmal deutlich im Posttest. Kann ich diesen Unterschied auch auf seine Signifikanz hin überprüfen?
Ich hoffe, du verstehst was ich meine und du kannst mir helfen!
Viele Grüße,
Julian
Hallo Julian,
Ich hoffe ich antworte nicht zu spät, leider kann ich dir grade nicht ganz folgen. Der Zweck des U-Test ist es ja schon zu schauen, ob sich die Stichproben in der Größe der Messwerte signifikant unterscheiden.
Ich würde noch empfehlen wenn du die Bedeutsamkeit deiner Ergebnisse beurteilen willst, solltest du Effektstärken berechnen. Zum Beispiel kann der Mittelwertsunterschied zwar signifikant sein, doch heißt dass nicht, dass er groß genug ist, um als bedeutsam eingestuft zu werden.
Methoden, um die Effektstärke zu messen sind Cohens d oder der Korrelationskoeffizient r von Pearson. Wenn sich deine Gruppen hinsichtlich ihrer Grösse stark unterscheiden, solltest du allerdings Cohens d nehmen.
Die folgende Einteilung ist dann anzuwenden:
r = .10 entspricht einem schwachen Effekt
r = .30 entspricht einem mittleren Effekt
r = .50 entspricht einem starken Effekt
Ich hoffe ich konnte dir helfen. Wenn ich dich falsch verstanden habe, dann ist es am besten zu erkläst kurz dein Design genauer.
Viele Grüße
Theresa
Hallo Theresa,
ich habe eine Gruppe (Athleten) die habe ich in Kontroll- und Interventionsgruppe aufgeteilt (zufällig nach der Gewölbeausprägung im Sprungbein).
Jetzt möchte ich wissen, ob sich durch mein Training die Interventionsgruppe in der Sprungleistung ( 5 einzeilne tests) verbessert hat.
Ich stehe einwenig auf dem Schlauch was den Test angeht den ich verwenden muss… Vorallem wenn ich, dass dann mit der Kontrollgruppe vergleichen will.
Also angenommen dirch die deskreptive Statistik sehe ich, dass es in der Interventionsgruppe eine Verbesserung von vorher zu nacher gibt. In der Kontrollgruppe sehe ich das auch, nur ist die Verbesserung geringer. Jetzt müsste ich dies ja statistisch überprüfen (reicht ein t -test?!). Kann ich dann die beiden Gruppen Kontroll und Intervention miteinander vergleichen?!
Vielen Dank
Und es wäre super, wenn du mir da weiterhelfen könntest.
Liebe Grüße
Caro
Hallo Caro,
Da deine Variablen vermutlich mindestens ordinalskaliert sind, kannst du sie nun auf Normalverteilung testen. Ist dies der Fall musst du auch noch die Gleichheit der Varianz testen (mittels Levane Test). Ist diese gegeben, kannst du dann den t-test anwenden ansonsten den Welch-Test Sind diese allerdings nicht normalverteilt eignet sich der Mann-Whitney U Testberichte (= Wilcoxon Rangsummentest).
Die Tests geben einen p-Wert aus. Ist der p-Wert kleiner 0,05, so gibt es einen signifikanten Unterschied. Ist der p-Wert größer als 0,05, so kann kein signifikanter Unterschied nachgewiesen werden. Dadurch ist aber noch nicht gesagt, dass es keinen gibt.
Ich hoffe ich konnte dir helfen.
Liebe Grüße
Theresa
Hallo Theresa,
in einem Pre-Post Testdesign habe ich 3 Gruppen (Kontroll + 2 Interventionsgruppen) gemessen, wobei jede Person nacheinander sowohl die Messungen der Kontrollgruppe, als auch der beiden Interventionsgruppen durchlaufen hat. Da mir hierdurch Werte von 3 Gruppen zu 2 Zeitpunkten vorliegen bin ich mir gerade etwas unschlüssig mit welchem statistischen Verfahren ich diese Fragestellung einer Unterscheidung der drei Gruppen am elegantesten untersuche. Hierzu folgende Überlegungen…
1. Einfaktorielle Varianzanalyse: Einfache Berechnung der Mittelwertsunterschiede der selbst errechneten Differenzen (pre-post)
2. Zweifaktorielle Varianzanalyse mit Messwiederholung auf einem Faktor:
Als Innersubjektfaktor die Pre- bzw. Postmessung und als Zwischensubjektfaktor die Gruppe
3. Zweifaktorielle Varianzanalyse mit Messwiederholung auf beiden Faktoren:
Als Innersubjektfaktor sowohl die zweifach gestufte Variable (Pre/Post) als auch die dreifachgestufte Variable (Gruppen) angeben und zuordnen. Aufgrund der Anordnung in SPSS kann ich dann jedoch keine Zwischensubjektfaktoren angeben, so dass mir kein Post-hoc Test berechnet werden kann.
Über super wenn du mir über das richtig(ere) Verfahren Aufschluss geben könntest.
LG
Steffen
Hallo Steffen,
Da du mehr als 2 Gruppen hast, solltest du die Zweifaktorielle Varianzanalyse nutzen. Vorteil hier ist auch, dass Wechselwirkungen zwischen den Faktoren geprüft werden, d.h. wenn die Haupteffekte z.B. nicht signifikant wären, dann könnte man imer noch einen Wechselwirkungseffekt, Interaktionseffekt oder auch einen Moderatoreffekt finden. Wenn du auch noch metrische unabhängige Variablen hinzunehen möchtest, dann solltest du die ANCOVA nutzen. Möchtest du außerdem noch mehrere abhöngige Variablen untersuchen, dann ist es eine MANOVA.
Ich denke mit der Zweifaktoriellen Varianzanalyse solltest du auf angemessene Ergebnisse kommen. Der folgende Link sollte dir bei der Bestimmung der Innersubjektfaktoren, bzw des Zwischensubjektfaktors helfen.
https://www.youtube.com/watch?v=3I1jmTL64uc
Ich hoffe ich konnte helfen.
Liebe Grüße
Theresa