Transformation – ja, aber…

Wie Daniela bereits in ihrem Artikel `Wozu brauchst Du eine Transformation Deiner Daten? ´ geschrieben hat, ist die Transformation eurer Datensätze um Verteilungsprobleme für die weitere Analyse zu minimieren, mathematisch kein Problem und keine Manipulation eurer Daten. Trotzdem bleibt da immer dieser bittere Beigeschmack!!

Ich möchte euch nun an einem Beispiel verdeutlichen, warum man im Bereich der Biologie und Medizin lieber zweimal hinschauen sollte, um auszuschließen, dass Heteroskedastizität und Abweichungen von der Normalverteilung nicht Ursachen im Versuchsaufbau haben.

(Der Datensatz ist angelehnt an einen tatsächlichen Fall)

Das Beispiel

Das Beispiel stammt aus der Phytomedizin.

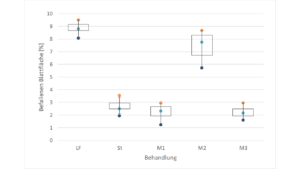Drei Versuchspräparate (M1-M3) werden gegen ein Pathogen (Pat) an einer anfälligen Sorte der Wirtspflanze (n=12) getestet. Die Mittel sollen in der Analyse mit einem Standard (St) und der Leerformulierung (LF) verglichen werden. Ermittelt wurde der Befall, als geschätzter prozentualer Anteil der Blattfläche. In vorausgegangenen in vitro Versuchen zeigten die Präparate alle mehr oder weniger eine direkte Wirkung auf das Pathogen.

An dieser Stelle werden einige bereits von ihren Betreuern gesagt bekommen: Du musst auf alle Fälle eine arcsin- Wurzeltransformation machen. Weil man das bei prozentualen Werten halt so macht, um die Verteilung vom Mittelwert unabhängig zu machen. Diese Aussage ist richtig, wenn ich es mit Wahrscheinlichkeiten zu tun habe oder Anteilen an immer der gleichen Menge. Warum das so ist zu erklären, würde an dieser Stelle zu weit führen. Es sei aber an die geliebte Stochastik in der Mittelstufe erinnert.

In unserem Fall könnten wir den Befall auch in cm²angeben, was aber in der Realität an der Logistik scheitert. Also wird in der Phytomedizin häufig der Befall geschätzt. Die Notwendigkeit einer arcsin-Wurzel Transformation besteht nicht.

Die Analyse

Bei der Betrachtung der Deskriptiven Statistik, hier dargestellt im Box-Plot, sind Probleme für die weitere Auswertung zu erkennen. Klar zu erkennen sind Varianzunterschiede zwischen den Gruppen. Da sind LF und M2 die keine bzw, nur eine geringe Wirkung gegen das Pathogen haben, deren Varianz des Befalls aber deutlich größer ist als in den Behandlungen mit sehr guter Wirkung. Zudem befindet sich St auf der Grenze zur Normalverteilung. Ein Effekt der gerade in den Extrembereichen häufiger vorkommt-Gesünder als Gesund geht nicht und Toter als Tot auch nicht!  Die Variabilität in einer Gruppe hat auf einer Seite eine natürliche Grenze, die Kurve wird schief.

Wir transformieren also die Daten. In unserem Fall zeigt eine Wurzeltransformation größtenteils die gewünschte Wirkung, zeigt aber auch ein Problem von Transformationen.

Bei Werten im mittleren Bereich ist der Effekt nicht so groß!

Das Varianzproblem von M2 wurde nicht behoben.

In einem Report könnte man jetzt argumentieren, dass der Effekt von M2 zu gering ist um von weiterem Interesse zu sein. Die ANOVA also nur im Vergleich, Leerformulierung, Standard, Mittel 1 und 3 durchgeführt wird. Bei der Betrachtung der Least significant difference erhält man sogar einen signifikanten Unterschied zwischen unseren Testmitteln M1 und M3 und dem Standard. Alles super also, und ein gutes Beispiel für eine Transformation die zum Erfolg geführt hat.

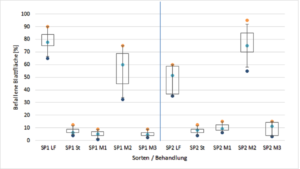Wenn da nicht noch Daten mit einer zweiten weniger anfälligen Sorte aus demselben Versuch wären, die alle unsere Überlegungen unter ein anderes Licht stellen.

Auf der linken Seite sind die Ergebnisse zu sehen, die wir bisher betrachtet haben. Auf der rechten Seite nun die Ergebnisse von Pflanzen, die zeitgleich unter gleichen Bedingungen mit Sorte 1 (SP1) angezogen und mit denselben Mittelansätzen behandelt wurden. Auf den ersten Blick fällt auf, dass sich das Verhältnis zwischen Leerformulierung und M2 verkehrt hat. Da die Sorte 2 (SP2) als weniger anfällig für das Pathogen gilt, ist das Ergebnis der Behandlung mit der Leerformulierung plausibel. Jedoch bedeutet das Ergebnis von M2, dass die Sorte zusammen mit der Behandlung einen negativen Effekt zeigt. Schaut man sich die Ergebnisse von M1 und M3 im Vergleich zur Sorte 1 an, wird deutlich, dass der negative Einfluss der Sorte 2 auch hier zu beobachten ist. Lediglich die Werte des Standards bleiben konstant.

Was heißt das nun für die Auswertung der Ergebnisse von Sorte 1?

Es muss davon ausgegangen werden, dass auch Sorte 1 einen wie auch immer gearteten Effekt auf die Wirksamkeit unserer Testpräparate (M1-M3) hat und wir es gegebenenfalls mit mehreren Wirkmechanismen zu tun haben. Da der Standard (St) keine Unterschiede im Sortenvergleich zeigt, spielt die Sortenwahl hier also keine Rolle. Somit ist dieser Standard zu mindestens Fragwürdig, da hier unterschiedliche Wirkmechanismen verglichen werden. Auch der Ausschluss von M2 aus der weiteren Analyse muss überdacht werden. Bei diesem Mittel scheint die Sortenauswahl einen besonders großen Einfluss zu haben. Bei Versuchen mit Mitteln die solche Abhängigkeiten von der individuellen Reaktion des Wirtsorganismus zeigen, ist eine Stichprobengröße von 12 viel zu wenig. Um eine verlässliche Aussage über das Potential von M2 zu tätigen sind erheblich größere Stichprobenumfänge von Nöten. In der Medizin wird meist darauf geachtet in vielen anderen Bereichen aus dem Feld der Life Sciences nicht.

Das Fazit

Schaut euch eure Datensätze genau an, hinterfragt euren Ansatz, überlegt ob ihr eure Varianz und Normalverteilung auch methodisch beeinflussen könnt.

Erst wenn ihr keine anderen Möglichkeiten seht, transformiert eure Daten, dann ist auch der bittere Beigeschmack weg!!!!